Operasi pada himpunan terdiri dari gabungan, irisan, komplemen, selisih, penjumlahan/beda setangkup, dan perkalian kartesian. Setiap operasi pada himpunan mempunyai suatu aturan yang digunakan untuk melakukan tindakan pada suatu himpunan. Dua himpunan atau lebih ini dapat dioperasikan sehingga menghasilkan himpunan baru. Perlakuan operasi yang melibatkan dua himpunan atau lebih disebut dengan operasi pada himpunan.
Pada dua buah bilangan dapat dilakukan operasi sehingga menghasilkan bilangan baru. Bentuk operasi antar bilangan dapat berupa penjumlahan (+), pengurangan (–), perkalian (×), atau pembagian ( : ). Pada dua himpunan atau lebih juga dapat dilakukan operasi yang dapat menghasilkan suatu himpunan baru. Bentuk operasi pada himpunan meliputi cara mendapatkan himpunan yang sama dari dua himpunan, gabungan dari dua himpupan, dan beberapa bentuk operasi pada himpunan lainnya.

Bagaimanakah aturan yang berlaku pada setiap bentuk operasi pada himpunan? Penjelasan masing-masing operasi pada himpunan diulas banyak melalui bahasan di bawah.
Table of Contents
Definisi Himpunan
Himpunan memuat kumpulan objek-objek yang anggotanya terdefinisi dengan jelas. Sebagai contoh, perhatikan dua definisi berikut:
- Kelompok siswa dengan tinggi lebih dari 150 cm
- Kelompok siswa berwajah cantik.
Definisi pertama yaitu kelompok siswa dengan tinggi lebih dari 150 cm merupakan definisi yang jelas. Di mana, definisi tersebut memuat himpunan semua siswa yang memiliki tinggi lebih dari 150 cm. Sementara siswa dengan tinggi kurang dari atau sama dengan 150 cm tidak masuk dalam himpunan tersebut.
Definisi pada pernyataan kedua yaitu kelompok siswa berwajah cantik bukan merupakan definisi yang jelas. Sebab wajah cantik tidak bersifat relatif dan tidak memiliki tolak ukur yang pasti.
Pernyataan pertama merupakan contoh himpunan, sedangkan definisi kedua bukan contoh himpunan. Mengapa? Alasannya ada pada pengertian himpunan. Pernyataan pertama memiliki anggota yang terdefinisi dengan jelas. Sedangkan pernyataan kedua tidak memiliki anggota dengan definisi yang jelas.
Baca Juga: Himpunan dan Diagram Venn
Operasi pada Himpunan
Bentuk operasi pada himpunan dapat berupa irisan, gabungan, selisih, komplemen, beda setangkup, dan perkalian kartesian. Cara melakukan operasi pada himpunan dari setiap bentuk operasi dijelaskan melalui penjelasan-penjelasan di bawah.
1) Irisan Himpunan/Intersection ( ∩ )
Irisan dari dua himpunan A dan B adalah himpunan dengan anggota-anggota yang sama-sama terdapat pada dua himpunan tersebut. Atau dapat dikatakan bahwa himpunan irisan memuat semua anggota-anggota yang sama dari himpunan A dan himpunan B.
Simbol himpunan beririsan dinyatakan dalam notasi ∩, dibaca irisan. Notasi pembentuk himpunan untuk irisan dua himpunan A dan B dinyatakan dalam persamaan A ∩ B = {x | x ∈ A dan x ∈ B}.
Sebagai contoh terdapat himpunan A = {a, b, c, d, e} dan B = {a, i, u, e, o}. Perhatikan bahwa ada dua anggota himpunan yang sama-sama terletak pada himpunan A dan B yaitu a dan e. Sehingga, irisan himpunan A dan himpunan B adalah a dan e yang dituliskan dalam simbol dengan A ∩ B = {a, e}.
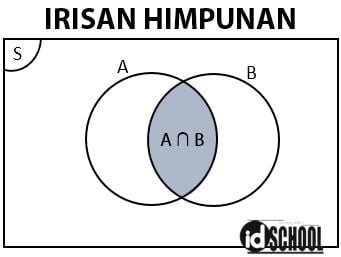
Contoh operasi pada himpunan yang mmerupakan irisan himpunan dapat dilihat seperti berikut.
- A = {a, b, c, d, e}
B = {a, i, u, e, o}
A ∩ B = {a, e}
- A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A ∩ B = {2, 3, 5}
Baca Juga: Pola Bilangan dan Rumus Un Pola Bilangan
2) Gabungan Himpunan/Union ( ∪ )
Operasi pada himpunan yang merupakan gabungan himpunan menyatakan operasi untuk menggabungkan anggota-anggota dari dua himpunan atau lebih menjadi sebuah himpunan baru. Anggota-anggota himpunan gabungan berasal dari semua anggota himpunan yang dioperasikan. Jika terdapat anggota himpunan yang sama cukup dituliskan satu kali.
Simbol untuk menyatakan gabungan himpunan adalah notasi ∪ (union) yang dibaca gabungan. Notasi pembentuk himpunan untuk gabungan dua himpunan A dan B dinyatakan dalam persamaan A ∪ B = {x|x ϵ A atau x ϵ B}.
Sebagai contoh, terdapat dua buah himpunan A dan B dengan A = {a, b, c, d, e} dan B = {a, i, u, e, o}. Operasi pada himpunan untuk gabungan kedua himpunan dilakukan dengan menggabungkan semnua anggota-anggotanya. Sehingga hasil dari gabungan himpunan A dan himpunan B adalah {a, b, c, d, e, i, u, o} yang dapat dinotasikan dengan A ∪ B = {a, b, c, d, e, i, u, o}.
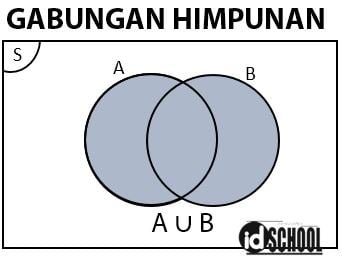
Contoh soal operasi gabungan himpunan diberikan seperti berikut.
- A = {a, b, c, d, e}
B = {a, i, u, e, o}
A ∪ B = {a, b, c, d, e, g, k}
- A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A ∪ B = {1, 2, 3, 4, 5, 7, 11}
Baca Juga: Cara Menentukan Satuan Bilangan Berpangkat Banyak
3) Selisih Himpunan/Difference ( – )
Selisih dua himpunan meliputi semua anggota himpunan yang tidak dimiliki himpunan lain. Selisih antara dua buah himpunan dinotasikan oleh tanda kurang ( – ). Notasi pembangkit untuk selisih dua himpunan A dan B ditulis dalam persamaan A – B = {x|x ϵ A atau x ∉ B}.
Pada selisih himpunan A – B, himpunan barunya berupa semua anggota A yang tidak ada pada B. Sedangkan selisih himpunan B – A, himpunan baru yang dihasilkan sama dengan anggota himpunan B yang tidak ada pada A.
Sebagai contoh, diketahui dua buah himpunan A = {a, b, c, d, e} dan B = {a, i, u, e, o}. Selisih dua himpunan A – B = {b, c, d}, sementara selisih dua himpunan B – A = {i, u, o}.
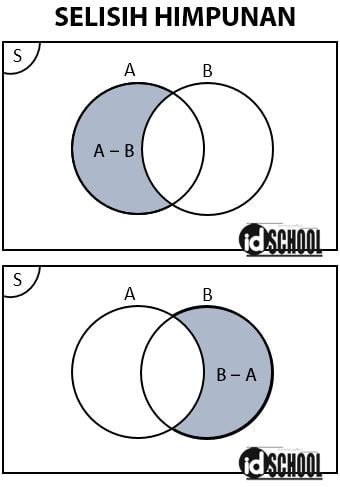
Contoh operasi pada himpunan untuk selisih himpunan:
- A = {a, b, c, d, e}
B = {a, i, u, e, o}
A – B = {b, c, d}
- A = {a, b, c, d, e}
B = {a, i, u, e, o}
B – A = {i, u, o}
- A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A – B = {1, 4}
Baca Juga: Himpunan Bagian dan Cara Menentukan Banyaknya
4) Komplemen Himpunan ( AC )
Komplemen dari sebuah himpunan A adalah himpunan semua anggota himpunan semesta (S) yang tidak ada di himpunan A. Notasi komplemen suatu himpunan dinyatakan dalam pangkat C yang melekat pada himpunan terkait.
Himpunan semesta memuat semua anggota dari himpunan yang dibicarakan. Sebagai contoh, cakupan himpunan semesta untuk bilangan ganjil adalah semua bilangan ganjil yang tak berhingga. Untuk cakupan himpunan semesta untuk lima bilangan ganjil pertama memuat himpunan dengan anggota-anggota 1, 3, 5, 7, dan 9.
Sementara komplemen suatu himpunan merupakan himpunan dengan anggota yang bukan merupakan anggota himpunan semesta.
Untuk sebuah himpunan A maka komplemen dari himpunan A dinyatakan dalam notasi AC (dibaca A komplemen). Notasi pembangkit untuk menyatakan pernyataan suatu himpunan komplemen adalah AC = {x| x ∉ A, x ∈ S}.

Contoh soal komplemen dari suatu himpunan:
- S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 3, 5, 7, 9}
AC = {2, 4, 6, 8, 10}
- S = {bilangan ganjil kurang dari 20}
A= {1, 3, …, 9}
Ac = {11, 13, 15, 17, 19}
- S = {1, 2, 3, 4, 5, 6, 7}
A = {1, 3, 5, 7}
Ac = {2,4,6}
Baca Juga: Relasi dan Fungsi (Pengertian + Perbedaan)
5) Beda Setangkup (Symmetric Difference)
Operasi himpunan beda setangkup menghasilkan himpunan baru dengan anggota-anggota yang bukan merupakan irisan dari himpunan-himpunan yang dioperasikan. Pada operasi beda setangkup himpunan A dan B akan menghasilkan suatu himpunan yang anggotanya ada pada himpunan A atau B tetapi tidak pada keduanya.
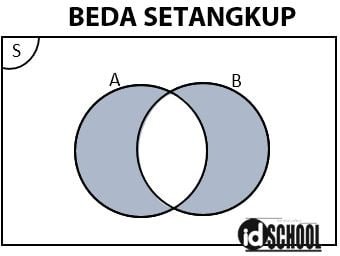
Notasi operator beda setangkup dinyatakan dalam sebuah tanda plus dalam sebuah lingkaran, ⊕. Notasi pembangkit untuk beda setangkup adalah A ⊕ B = {x | x ∈ A tetapi x ∉ B dan x ∈ B tetapi x ∉ A}. Pernyataan tersebut sama dengan A ⊕ B = (A ∪ B) – (A ∩ B) atau sama dengan A ⊕ B = (A – B) ∪ (B – A).
Sebagai contoh diketahui dua buah himpunan A = {a, b, c, d, e} dan B = {a, i, u, e, o}. Anggota-anggota himpunan A dan B yang sama meliputi a dan e (irisan kedua himpunan). Hasil operasi beda setangkup merupakan anggota himpunan A atau B tetapi tidak keduanya.
Jadi, himpunan baru hasil operasi himpunan beda setangkup untuk himpunan A dan himpunan B adalah b, c, d, i, u, dan o yang dapat dinotasikan dengan A ⊕ B = {b, c, d, i, u, o}.
Contoh operasi himpunan beda setangkup:
- A = {a, b, c, d, e}
B = {a, i, u, e, o}
A ⊕ B = {b, c, d, i, u, o}
- A = {1, 2, 3, 4, 5}
B = {2, 3, 5, 7, 11}
A ⊕ B = {1, 4, 7, 11}
Operasi himpunan beda setangkup memenuhi hukum komutatif (A + B = B + A) dan asosiatif: (A + B) + C = A + (B + C).
Baca Juga: Bentuk Soal Diagram Venn pada Tes Potensi Akademik
6) Perkalian Kartesian (Cartesian Product)
Operasi pada himpunan untuk perkalian kartesian berupa pasangan berurutan. Misalnya pada perkalian kartesian dari himpunan A dan B, hasil himpunan barunya adalah semua pasangan berurut yang dibentuk dari anggota – angota himpunan A dan B. Simbol notasi perkalian kartesian himpunan A dan B dinyatana melalui A × B.
Sebagai contoh, diketahui dua buah himpunan A = {1, 2, 3} dan B ={a, b}. Himpunan hasil operasi perkalian kartesiannya adalah A × B = {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)}.
Notasi pembangkit untuk himpunan hasil operasi perkalian kartesian untuk himpunan A dan B adalah A × B = {(a, b) | a ∊ A dan b ∊ B}.
Contoh operasi himpunan untuk perkalian kartesian:
- A = {1, 2, 3}
B = {7, 9}
A × B = {(1,7), (1,9), (2,7), (2,9), (3,7), (3,9)}
- F = {bakso, soto, mie ayam}
D = {es teh, es jeruk, kopi}
F × D = {(bakso, es teh), (bakso, es jeruk), (bakso, kopi), (soto, es teh), (soto, es jeruk), (soto, kopi), (mie ayam, es teh), (mie ayam, es jeruk), (mie ayam, kopi)}
Pada operasi perkalian kartesian tidak berlaku A × B = B × A, karena anggota (a, b) tidak sama dengan (b, a).
Demikianlah tadi ulasan materi operasi pada himpunan yang meliputi irisan, gabungan, selisih, komplemen, beda setangkup, dan kartesian. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Cara Menentukan Banyaknya Pemetaan
