Rumus Berpapasan dan Menyusul +Contoh Soalnya

Rumus berpapasan dan menyusul merupakan pengembangan dari rumus jarak, waktu, dan kecepatan. Ada tiga rumus berpapasan dan menyusul yang perlu kamu ketahui. Pertama untuk kondisi saat berpapasan dengan waktu berangkat sama. Kedua untuk waktu berpapasan dengan waktu berangkat yang berbeda. Ketiga adalah kapan waktu menyusul.

Seseorang atau benda yang bergerak memiliki besaran kecepatan, jarak, dan waktu. Rumus rumus kecepatan adalah K = ^J/_w, rumus jarak adalah J = K × W, dan rumus waktu adalah w = ^J/_K.

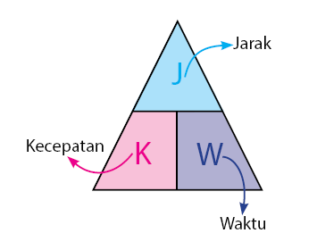
Pengetahuan mengenai rumus jarak, waktu, dan kecepatan dibutuhkan untuk mendapatkan rumus berpapasan dan menyusul. Lebih lanjut mengenai rumus berpapasan dan menyusul ada di bawah.

Daftar isi:

• Rumus Berpapasan
  • 1) Waktu Berangkat Sama + Contoh Soal
  • 2) Waktu Berangkat Berbeda + Contoh Soalnya
• Rumus Menyusul
  • Contoh Soal 3.1
  • Contoh Soal 3.2

Rumus Berpapasan

Rumus berpapasan dibedakan menjadi dua yaitu saat dua benda bergerak dari dua titik berbeda dengan waktu berangkat yang sama dan waktu berangkat berbeda. Rute atau jalan yang dilalui sama sehingga kedua objek yang bergrak akan berpapasan di suatu titik.

1) Waktu Berangkat Sama + Contoh Soal

Bahasan rumus berpapasan dan menyusul yang pertama adalah rumus berpapasan untuk dua benda dari dua titik berlawanan dengan waktu berangkat sama dan kecepatan berbeda.

Sebuah mobil merah dan mobil biru berangkat pada waktu yang sama. Kedua mobil berangkat dari dua titik berbeda dan akan melintasi rute yang sama. Mobil merah dan mobil biru tersebut akan bertemu setelah berjalan pada selang waktu tertentu. Misalkan waktu berangkat mobil merah adalah w₁ dengan keceatan K₁. Sementara mobil biru berangkan pada waktu w₂ dengan kecepatan K₂. Kedua mobil kemudian akan bertemu setelah selang waktu w_p.

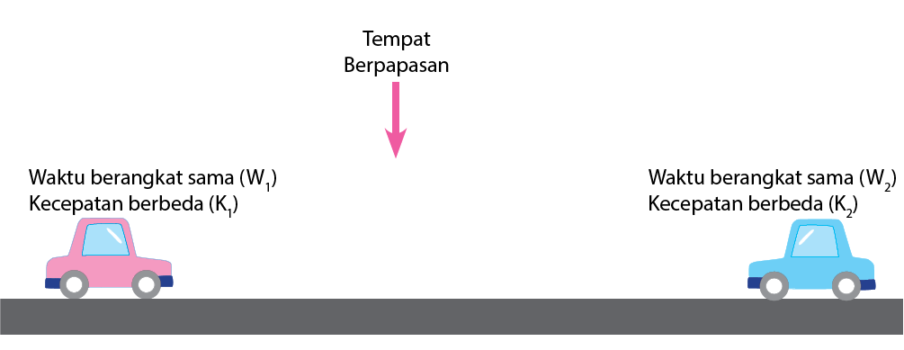
Jarak yang ditempuh mobil merah dari titik berangkatnya ke titik keberangkatan mobil biru sama dengan jarak titik keberangkatan mobil biru ke titik keberangkatan mobil merah. Artinya, jarak total yang akan ditempuh mobil merah sama dengan mobil biru. Sehingga, jarak total = jarak yang ditempuh mobil merah + jarak yang ditempuh mobil biru.

• Jarak yang ditemuh
  • mobil merah = K₁ × w_p
  • mobil biru = K₂ × w_p

Selanjutnya,

Jarak total = K₁ × w_p + K₂ × w_p

Jarak total = (K₁ + K₂)× w_p

Diperoleh rumus untuk menentukan waktu berpapasan saat waktu keberangkaran sama:

Keterangan simbol pada rumus berpapasan dan menyusul di atas:
w_p : Waktu berpapasan
K₁ : Kecepatan orang pertama
K₂ : Kecepatan orang kedua

Bagaimana cara menggunakan rumus berpapasan dan menyusul terdapat pada langkah penyelesaian soal di bawah.

Contoh Soal 1:

Dodi mengendarai sepeda dari rumahnya ke rumah Amar dengan jarak tempuh 10 km. Dari arah yang berlawanan, Amar mengendarai sepeda menuju rumah Dodi. Kecepatan Dodi dan Amar berturut-turut adalah 18 km/jam dan 12 km/jam.

Jika keduanya sama-sama berangkat pukul 09.00, maka mereka akan berpapasan pukul ….

Pembahasan:
Keterangan yang diberikan pada soal memberikan informasi-informasi seperti berikut.

• Diketahui:
  • Jarak tempuh = jarak total = 10 km
  • Kecepatan Dodi: K₁ = 18 km/jam
  • Kecepatan Amar: K₂ = 12 km/jam

Mencari waktu berpapasan (w_p) :

Dodi dan Amar berpapasan setelah keduanya menempuh perjalanan selama 20 menit. Jadi, Dodi dan Amar berpapasan pada pukul 09.00 + 0.20 = 09.20

2) Waktu Berangkat Berbeda + Contoh Soalnya

Bahasan rumus berpapasan dan menyusul yang berikutnya adalah rumus berpapasan untuk dua benda dari titik berlawanan yang berangkat dengan waktu dan kecepatan berbeda.

Mobil merah akan menuju titik keberangkatan mobil biru, sedangkan mobil biru akan berangkan menuju titik keberangkatan mobil merah. Kedua mobil melalui rute jalan yang sama sehingga akan berpapasan setelah selang waktu w_p.

Misalkan mobil biru berangkat pada pukul w₂ dengan kecepatan K₂. Setelah mobil biru menempuh jarak tertentu, mobil merah berangkat pada waktu w₁ dengan kecepatan K₁.

Mobil merah dan mobil biru berpapasan pada waktu w_p. Jarak yang ditempuh mobil biru sama dengan jarak yang ditembuh mobil biru sebelum mobil merah berangkat (K₂ × selisih waktu berangkat) + K₂ × w_p. Dan jarak yang ditempuh mobil merah sama dengan K₁ × w_p.

Selanjutnya,

Jarak total = K₁ × w_p + (K₂ × w_p + K₂ × selisih waktu berangkat)

Jarak total = w_p × (K₁ + K₂) + K₂ × selisih waktu berangkat

Sehingga,

w_p × (K₁ + K₂) = Jarak total – K₂ × selisih waktu berangkat

Diperoleh rumus untuk menentukan waktu berpapasan saat dua objek bergerak memilki waktu berangkat yang berbeda:

Keterangan simbol pada rumus berpapasan dan menyusul di atas:
w_p : Waktu berpapasan
K₁ : Kecepatan orang pertama
K₂ : Kecepatan orang kedua

Baca Juga: Skala, Jarak pada Peta, dan Jarak Sebenarnya

Contoh Soal 2

Dodi mengendarai sepeda dari rumahnya ke rumah Amar dengan jarak tempuh 18 km. Dari arah yang berlawanan, Amar mengendarai sepeda menuju rumah Dodi. Kecepatan Dodi dan Amar berturut-turut adalah 16 km/jam dan 12 km/jam.

Jika Dodi berangkat pukul 08.00 dan Amar berangkat pukul 08.15 maka mereka akan berpapasan pukul ….

Pembahasan:
Dari soal diberikan beberapa informasi seperti berikut.

• Diketahui:
  • Kecepatan Dodi: K₁ = 16 km/jam
  • Kecepatan Amar: K₂ = 12 km/jam
  • Jarak total = 18 km
  • Selisih waktu berangkat
    Δt = 08.15 – 08.00 = 0.15 menit
    Δt = ¹⁵/₆₀ jam = ¹/₄ jam

Mencari waktu berpapasan (w_p):

Pukul berpapasan diperoleh dari waktu keberangkatan orang ke dua (Amar) ditambah waktu berpapasan (w_p). Jadi, Dodi dan Amar berpapasan pada pukul 08.15 + 0.30 = 08.45

Baca Juga: Rumus Volume dan Luas Permukaan Tabung

Rumus Menyusul

Rumus berpapasan dan menyusul berikutnya adalah rumus untuk menyelesaikan masalah dengan kondisi titik berangkat sama dengan kecepatan dan waktu berangkan yang berbeda.

Mobil merah dan mobil biru berangkat dari titik yang sama. Mobil biru berangkat lebih dulu dengan waktu w₂ dan kecepatan K₂. Setelah mobil biru mencapai jarak tertentu, mobil merah berangkat dari titik yang sama pada waktu w_p dan kecepatan K₂.

Diketahui bahwa kecepatan mobil merah lebih besar dari kecepetan mobil biru (K₁ > K₂). Sehingga mobil merah akan menyusul mobil biru setelah selang waktu tertentu.

Misalkan waktu saat mobil merah menyusul (menyalip) mobil biru adalah w_m. Saat mobil merah tepat menyusul mobil biru maka jarak yang ditempuh mobil merah sama dengan jarak yang ditempuh mobil biru. Jarak yang ditempuh mobil merah = w_m × K₁ dan jarak yang ditempuh mobil biru = selisih waktu berangkat × K₂ + w_m × K₂.

Sehingga,

Jarak yang ditempuh mobil merah = Jarak yang ditempuh mobil biru

w_m × K₁ = w_m × K₂ + selisih waktu × K₂

w_m × K₁ – w_m × K₂ = K₂ × selisih waktu

(K₁ – K₂) × w_m = K₂ × selisih waktu

Diperoleh rumus menyusul:

Keterangan simbol pada rumus berpapasan dan menyusul di atas.
w_m : Waktu menyusul
K₁ : Kecepatan orang pertama
K₂ : Kecepatan orang kedua

Contoh Soal 3.1

Hanif mengendarai sepeda motor dengan kecepatan 45 km/jam. Ia berangkat pada pukul 06.55. Athar berangkat pada pukul 07.15 dengan tujuan dan rute yang sama. Jika Athar mengendarai mobil dengan kecepatan rata-rata 60 km/jam, maka ia bisa menyusul hanif pada pukul?

Pembahasan:
Dari soal diberikan beberapa informasi berikut.

• Diketahui:
  • Selisih waktu berangkat Hanif dan Athar
    = 07.15 – 06.55
    = 0.20 = ²⁰/₆₀ jam = ¹/₃ jam
  • Kecepatan sepeda motor Hanif: K₁ = 45 km/jam
  • Kecepatan mobil Athar: K₂ = 60 km/jam

Mencari waktu menyusul (w_m):

Waktu saat Athar dapat menyusul Hanif = 07.15 + 01.00 = 08.15. Jadi, Athar dapat menyusul Hanif pada pukul 08.15 (satu jam setelah Athar berangkat).

Contoh Soal 3.2

Dua bus akan sama-sama menuju Kota Bandung yaitu Bus A dan Bus B. Kedua bus tersebut akan melalui rute yang sama. Bus A berangkat dari terminal Yogyakarta dengan kecepatan 60 km/jam. Sedangkan bus B berangkat dari Yogyakarta dengan kecepatan 75 km/jam.

Jika bus A berangkat pukul 13.00 dan bus B berangkat pukul 15.30 maka bus B dapat menyusul bus A pada pukul ….

Pembahasan:
Dari keterangan yang diberikan dapat diperoleh nilai-nilai berikut.

• Diketahui:
  • Selisih waktu berangkat bus A dan bus B
    = 15.30 – 13.00
    = 2.30 = 2¹/₂ jam
  • Kecepatan bus A: K₁ = 60 km/jam
  • Kecepatan bus B: K₂ = 75 km/jam

Mencari waktu menyusul:

Pukul berpapasan diperoleh dari waktu berangkat bus ke dua (bus B) ditambah waktu menyusul, yaitu 15.30 + 10.00 = 25.30. Karena dalam satu hari hanya ada 24 jam, maka Bus B dapat menyusul Bus A pada pukul 25.30 – 24.00 = 01.30 di kemudian harinya (sudah berganti hari).

Sekian pembahasan mengenai rumus berpapasan dan menyusul. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Rumus Debit Volume Waktu