Rumus bunga tunggal adalah hasil kali persen bunga, lama waktu pembungaan, dan modal (tabungan atau pinjamin). Untuk persen bunga adalah b, lama waktu pembungaan adalah n, dan besar modal adalah M. Rumus bunga tunggal adalah B = b% × t × M.
Persentase bunga tunggal diberikan dalam setahun, misalnya 6% persen per tahun. Saat lama waktu menabung kurang dari satu tahun (n bulan). Rumus bunga tunggal menjadi B = b% × n/12 × M.
Soal mengenai bunga tunggal dapat beragam. Beberapa soal yang sering ditanyakan adalah menanyakan berapa besar bunga, persentase per tahun, lama waktu menabung, atau besar modal.
Bagaimana cara menghitung besar bunga tunggal? Bagaimana cara menghitung persentase bunga, lama waktu menabung, atau besar tabungan awal (modal)? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
- Rumus Bunga Tunggal
- Cara Menghitung Besar Bunga Tunggal
- Cara Menghitung Lama Waktu Menabung
- Contoh Soal dan Pembahasan
Rumus Bunga Tunggal
Bunga adalah imbalan yang diberikan dalam sebuah transaksi tabungan dan hutang. Bunga tunggal adalah sebuah sistem pemberian imbalan dengan nilai yang tetap selama selang periode tertentu sesuai kesepakatan. Pada sistem bunga tunggal, besar bunga hanya mengenai besar tabungan atau pinjaman saja.
Sistem bunga tunggal yang mengenakan memberikan bungan untuk sejumlah besar bunga yang diperoleh di periode sebelumnya merupakan sistem bunga majemuk. Namun sistem bunga majemuk tidak akan dibahas di sini. Pembahasan mengenai sistem bunga majemuk ada di halaman rumus bunga majemuk.
Kembali ke bahasan sistem bunga tunggal.
Misalkan sebuah instansi menetapkan besar bunga kepada setiap nasabah sebesar b% per tahun. Rumus bunga tunggal yang berlaku untuk lama waktu 1 bulan dan m bulan.
Persamaan di bawah menyatakan besar bunga tunggal yang akan diperoleh.
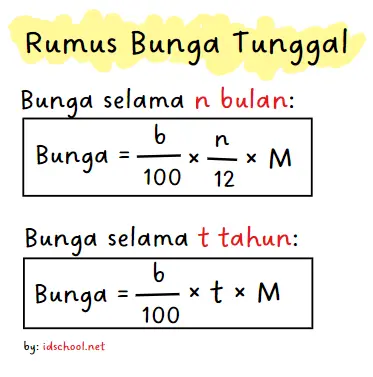
Keterangan:
B = besar bunga yang diperoleh
b = persentase bunga tunggal
n = lama waktu menabung (dalam bulan)
t = lama waktu menabung (dalam tahun)
Mo = modal (tabungan awal atau pinjaman)
Baca Juga: Persentase Untung/Rugi
Bagaimana cara menghitung besar bunga tunggal dan lama menabung terdapat pada dua bahasan di bawah.
Cara Menghitung Besar Bunga Tunggal
Bagaimana cara menghitung besar bunga tunggal akan ditunjukkan melalui penyelesaian sebuah contoh berikut.
Soal:
Andi menabung di bank Rp5.000.000,00 dengan bunga tunggal 6% per tahun. Hitunglah:
a) Besar bunga untuk setiap tiga bulan
b) Besar bunga selama 16 bulan
c) Besar bunga yang diterima selama setahun
Jawab:
Dari soal dapat diperoleh nilai-nilai berikut.
- Diketahui:
- Tabungan awal: M = Rp5.000.000,00
- Besar bunga tunggal: b = 6% per tahun
Rumus bunga tunggal yang diperoleh selama n bulan:
a) Bunga yang diterima setiap 3 bulan
b) Bunga yang diterima setelah 16 bulan
Rumus bunga tunggal yang diperoleh selama t tahun:
c) Bunga yang diterima setelah 1 tahun
Bunga = 6 × 50.000 = Rp300.000,00
Baca Juga: Cara Tahu Berapa Harga Sebelum Diskon
Cara Menghitung Lama Waktu Menabung
Bagaimana cara mengetahui lama waktu menabung agar besar tabungan mencapai suatu nilai tertentu akan ditunjukkan melalui sebuah langkah penyelesaian masalah di bawah.
Soal:
Bank Berdikari menawarkan tabungan dengan suku bunga tunggal sebesar 5% per tahun. Jika Bina menabung di Bank Berdikari sebesar Rp10.000.000,00, maka tabungan Binar akan menjadi Rp20.000.000,00 setelah … tahun.
Pembahasan:
Berdasarkan keterangan pada soal dapat diperoleh informasi berikut.
- Diketahu:
- Besar suku bunga tunggal: b = 5% per tahun
- Tabungan awal:
Modal = Rp10.000.000,00 - Tabungan akhir:
Modal + Bunga = Rp20.000.000,00
Besar bunga yang diterima
= Rp20.000.000,00 – Rp10.000.000,00
= Rp10.000.000,00
Menentukan lama waktu menabung:
Jadi, lama waktu Bina menabung saat tabungannya menjadi Rp20.000.000,00 adalah 20 tahun.
Baca Juga: Aritmatika Sosial
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan soal tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh Soal 1 – Besar Bunga Setelah n Bulan
Ayah menabung di Bank Kaya Raya sebesar 10.500.000 rupiah. Jika bank tersebut menerapkan bunga tunggal 12% per tahun, maka jumlah tabungan ayah seterlah 7 bulan adalah … rupiah.
A. 13.400.000
B. 12.350.000
C. 12.325.000
D. 11.523.000
E. 11.235.000
Pembahasan:
Dari informasi yang diberikan dapat diketahui beberapa nilai seperti berikut.
- Diketahui:
- Tabungan awal: M = Rp10.500.000,00
- Besar bunga tunggal: b = 12% per tahun
- Lama waktu menabung: n = 7 bulan
Menghitung besar bunga selama 7 bulan:
Bunga = 7 × 105.000 = 735.000
Jadi, jumlah tabungan ayah seterlah 7 bulan = 10.500.000 + 735.000 = 11.235.000 rupiah.
Jawaban: E
Contoh Soal 2 – Lama Waktu Menabung
Bank A menawarkan bunga tunggal dengan suku bunga sebesar 5% per tahun. Jika Mr X menabung perdana sebesar Rp50.000.000,00 di Bank A, maka setelah berapa bulan tabungan akhirnya menjadi Rp55.000.000,00?
A. 12
B. 14
C. 18
D. 24
E. 36
Pembahasan:
Dari informasi yang diberikan dapat diperoleh nilai-nilai berikut.
- Diketahui:
- Besar suku bunga tunggal: b = 5% per tahun
- Tabungan awal: M = Rp50.000.000,00
- Tabungan akhir = Rp55.000.000,00
- Lama waktu menabung = n bulan
Besar bunga yang diterima setelah n buna
= 55.000.000 – 50.000.000
= 5.000.000
Menghitung lama waktu menabung (n):
Jadi, tabungan Mr X akhirnya menjadi Rp55.000.000,00 setelah 24 bulan.
Jawaban: D
Sekian, ulasan rumus bunga tunggal dan majemuk dalam arimatika sosial. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
