Permutasi adalah banyak cara menyusun beberapa obyek dengan memerhatikan urutan. Ada lima rumus permutasi yang perlu diketahui. Rumus permutasi r obyek dari n obyek, permutasi siklis, dan permutasi untuk k1, k2, …, kn elemen yang sama dari n elemen adalah n!/k1 · k2 · … · kn.
Selain itu ada rumus permutasi saat terdapat pengulangan elemen dan permutasi saat pengulangan elemen tidak dibolehkan. Pembahasan detail rumus permutasi ada di bawah.
Daftar isi:
Contoh Masalah Permutasi
Contoh permutasi adalah susunan pengurus kelas yang terdiri dari ketua dan sekretaris. Saat ada tiga siswa yang akan dipilih menjadi pengurus. Misalkan ketiga siswa tersebut adalah Aisyah, Beni, dan Chila.
Susunan pengurus yang mungkin adalah {Aisyah, Beni}; {Aisyah, Chila}; {Beni, Aisyah}; {Beni, Chila}; {Chila, Aisyah}; dan {Chila, Beni}. Pada permutasi, susunan {Aisyah, Beni} berbeda dengan susunan {Beni, Aisyah}. INGAT!! Karena pada permutasi memerhatikan susunan.
Susunan untuk {Aisyah, Beni} berarti jabatan ketua = Aisyah dan wakil = Beni. Sedangkan susunan untuk {Beni, Aisyah} berarti jabatan ketua = Beni dan wakil = Aisyah. Jadi, banyak susunan pengurus kelas yang terdiri dari ketua dan sekretaris ada 6.
Baca Juga: Perbedaan Permutasi dan Kombinasi
5 Rumus Permutasi
Ringkasan lima rumus permutasi yang perlu diketahui terdapat pada tabel di bawah.
| Jenis permutasi | Rumus permutasi |
| Permutasi r elemen dan n elemen | nPr = n!/(n‒r)! |
| k1, k2, k3, …, kr unsur sama | nPk1, k2, …, kr = n!/k1!·k2!·…·kr! |
| Siklis | P(siklis, n) = (n ‒1)! |
| Pengulangan elemen tidak diperbolehkan | n · (n-1) · (n-2) · … · 3 · 2 · 1 = n! |
| Pengulangan elemen diperbolehkan | nr |
Penjelasan lebih banyak mengenai lima rumus permutasi di atas terdapat ada di bawah.
1) Rumus Permutasi r elemen dari n elemen (r < n)
Rumus permutasi r elemen dari n elemen adalah P(n, r) = nPr = (nr) = n!/(n‒r)! Rumus ini digunakan untuk mengetahui banyak susunan r elemen yang dapat dibentuk oleh n elemen.

Contoh soal rumus permutasi r elemen dari n elemen adalah banyak susunan pengurus. Misalnya pada banyak susunan pengurus untuk ketua, wakil, dan bendahara dari 10 siswa.
Susunan pengurus terdiri dari r = 3 elemen dari n = 10 elemen yang tersedia. Rumus permutasi yang sesuai adalah 10P3. Cara menghitungnya dilakukan seperti berikut.
2) Rumus Permutasi k1, k2, …, kr unsur yang sama
Permutasi n elemen dengan k1, k2, …, kr unsur yang sama memiliki banyak susunan nPk1, k2, …, kr = n!/k1!·k2!·…·kr! dengan n = k1 + k2 + … + kr. Contoh permutasi k1, k2, …, kr unsur yang sama terdapat pada susunan berbeda yang dapat dibuat dari huruf-huruf dari suatu kata.
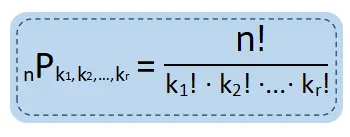
Cara menggunakan rumus permutasi k1, k2, …, kr unsur yang sama ada pada penyelesaian contoh soal permutasi nomor 3 di akhir pembahasan.
3) Rumus Permutasi Siklis
Rumus permutasi siklis adalah P(siklis, n) = (n ‒ 1)! Rumus ini digunakan untuk mengetahui banyak susunan yang dibentuk n obyek yang disusun melingkar.
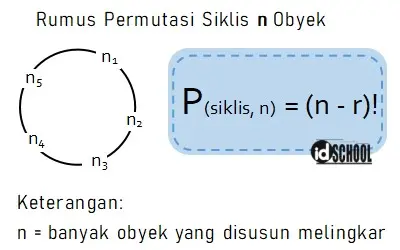
Contoh permutasi siklis terdapat pada susunan siswa yang sedang berdiskusi pada sebuah meja bundar. Cara menggunakan rumus permutasi siklis adalah pada penyelesaian contoh soal permutasi nomor 4 di akhir bahasan ini.
4) Permutasi untuk pengulangan elemen tidak diperbolehkan
Rumus permutasi untuk pengulangan elemen tidak diperbolehkan adalah n · (n-1) · (n-2) · … · 3 · 2 · 1 = n! Notasi n! adalah operasi hitung n faktorial yaitu perkalian bilangan asli sampai ke n.
Cara menggunakan rumus ini ada pada langkah penyelesaian di bawah.
Soal:
Dari angka-angka 1, 2, 3, 4, 5, dan 6 akan disusun nomor PIN yang terdiri dari empat angka. Tentukan banyak nomor PIN berupa bilangan >4.000 yang dapat disusun dengan tidak ada angka yang berulang!
Jawab:
Nomor PIN terdiri dari empat angka. Sehingga perlu menyusun empat digit angka.
Susunan nomor PIN berupa bilangan >4.000 dengan tidak ada angka yang berulang. Pengisian bilangan untuk keempat digit menyesuaikan kondisi berikut.
| Digit ke- | Angka yang dapat menempati |
| 1 | 4, 5, dan 6 karena PIN berupa bilangan >4.000 → n1 = 3 |
| 2 | 1, 2, 3, 4, 5, dan 6 (enam angka) dikurangi satu angka karena sudah dipakai pada digit pertama → n1 = 5 |
| 3 | sebanyak enam angka dikurangi dua karena dua angka sudah dipakai pada digit pertama dan kedua → n3 = 4 |
| 4 | sebanyak enam angka dikurangi tiga karena tiga angka sudah dipakai pada digit pertama, kedua, dan ketiga → n4 = 3 |
Jadi, banyak nomor PIN dengan bilangan > 4.000 yang dapat disusun dengan tidak ada angka yang berulang adalah n1 · n2 · n3 · n4 = 3 · 5 · 4 · 3 = 180.
5) Permutasi untuk pengulangan elemen diperbolehkan
Saat pengulangan elemen diperbolehkan, banyak susunan yang mungkin adalah perkalian banyak elemen sebanyak r kali. Misalkan tersedia n elemen yang menusun r tempat.
Permutasi saat pengulangan elemen diperbolehkan menjadi sebanyak n × n × … × n (perkalian n sebanyak r kali).
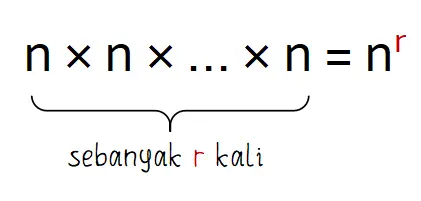
Contoh masalah permutasi untuk pengulangan elemen diperbolehkan adalah banyaj susunan sandi dengan angka yang boleh berulang. Misalnya, sebuah santi terdriri dari enam angka.
Semua angka yang dapat menempati digit sandi adalah bilangan nol sampai sembilan (n = 10). Sehingga banyak susunan sandi yang dapat dibuat adalah nr = 106 = 1.000.000 susunan.
Contoh Soal dan Pembahasan
Beberapa bentuk contoh soal permutasi ada di bawah.
Contoh 1 – Banyak susunan pengurus yang dapat dibentuk
Dari 8 orang calon pengurus karang taruna akan dipilih satu orang ketua, satu orang sekretaris, dan satu orang bendahara. Banyak susunan pengurus yang dapat dibentuk adalah ….
A. 56
B. 120
C. 210
D. 336
E. 343
Pembahasan:
Ada tiga jabatan yang akan dijabat dari 8 calon. Sehingga rumus permutasi yang digunakan adalah 8P3.
Menghitung nilai 8P3:
Jadi, banyak susunan pengurus yang dapat dibentuk adalah 336.
Jawaban: D
Baca Juga: Cara Menentukan Nilai n pada Notasi Faktorial
Contoh 2 – Banyak bilangan ratusan ganjil
Banyak bilangan ratusan ganjil yang dapat disusun dari angka-angka 0, 1, 2, 3, 4, dan 5 adalah ….
A. 60
B. 90
C. 108
D. 120
E. 216
Pembahasan:
Banyak bilangan ratusan ganjil memiliki tiga digit angka yang bisa berulang. Angka-angkan yang dapat menempati digit adalah 0, 1, 2, 3, 4, dan 5.
Ketentuan angka-angka yang bisa menempati digit ke-1, 2, dan 3:
| Digit ke- | Angka yang dapat menempati |
| 1 | semua angka bisa menempati kecuali 0 karena saat nol berada pada digit pertama maka nilai bilangan bukan lagi menjadi ratusan namun puluhan → n1 = 5 |
| 2 | semua angka bisa menempati → n2 = 6 |
| 3 | 1, 3, dan 5 agar nilai bilangan menjadi ganjil → n3 = 3 |
Jadi, banyak bilangan ratusan ganjil yang dapat disusun dari 0, 1, 2, 3, 4, dan 5 adalah n1 · n2 · n3 = 5 · 6 · 3 = 90.
Jawaban: B
Contoh 3 – Banyak susunan berbeda yang dapat dibuat dari huruf-huruf
Banyak susunan berbeda yang dapat dibuat dari huruf-huruf pada kata “KALKULUS” adalah ….
A. 1.680
B. 5.040
C. 8.400
D. 10.080
E. 20.160
Pembahasan:
Kata “KALKULUS” terdiri dari 8 huruf (n = 8) yang terdiri dari 2 huruf K (k1 = 2), 1 huruf A (k2 = 1), 2 huruf L (k3 = 2), 2 huruf U (k4 = 2) dan 1 huruf S (k5 = 1).
Banyak susunan berbeda dihitung dengan rumus permutasi k1, k2, k3, k4, dan k4 unsur sama seperti berikut.
Jadi, banyak susunan berbeda yang dapat dibuat dari huruf-huruf pada kata “KALKULUS” adalah 5.0440
Jawaban: B
Contoh 4 – Banyak susunan duduk melingkar
Banyak cara 7 orang akan duduk secara melingkar jika 4 orang harus selalu duduk berdampingan adalah ….
A. 210
B. 144
C. 72
D. 24
E. 6
Pembahasan:
Dari soal diketahui banyak obyek ada 7 orang yang duduk secara melingkar dengan 4 orang harus selalu duduk berdampingan. Cara duduk melingkar untuk 4 orang dianggap 1 sehingga menjadi permutasi (7 − 4) + 1 = 4 obyek.
Cara empat orang yang selalu duduk perdampingan adalah 4! dan permutasi 4 obyek adalah P(siklis, 4) = 3!
Jadi, banyak cara 7 orang akan duduk secara melingkar jika 4 orang harus selalu duduk berdampingan = 4! · P(siklis, 4) = 4! · 3! = 4 · 3 · 2 · 1 · 3 · 2 · 1 = 144 cara.
Jawaban: B
Demikianlah tadi ulasan rumus permutasi berserta cara menghitungnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Soal Tes Potensi Skolastik Duduk Melingkar
