Resistor (R), induktor (L), dan kapasitor dapat dirangkai dalam sebuah rangkaian listrik secara seri, paralel, atau gabungan. Suatu rangkaian listrik yang memuat resistor, induktor, dan kapasitor dikenal sebagai rangkaian RLC. Resistor adalah komponen listrik yang mempunyai fungsi untuk menghambat arus listrik. Sedangkan induktor dan kapasitor merupakan alat yang dapat menyimpan energi untuk sementara waktu. Perbedaan induktor dan kapasitor terletak pada jenis energi yang disimpan berupa medan magnet (induktor) atau muatan listrik (kapasitor).
Bentuk rangkaian RLC seri yang dihubungkan dengan sumber tegangan AC (Alternating Current) atau arus bolak-balik sesuai pada contoh berikut.

Baca Juga: 5 Macam Alat Ukur Listrik, Apa Saja?
Pada rangkaian AC RLC seri, besar arus listrik pada setiap komponen adalah sama (IR = IL = IC) dan memeuhi persamaan I = Imax · sin ωt. Nilai arus efektif (Ief) adalah akar dari nilai rata-rata kuadrat arus atau rms (root mean square) yang memenuhi persamaan Imax = Ief√2.
Arus listrik akan melewati ketiga komponen sehingga muncul tegangan VR (pada resistor), VL (pada induktor), dan VC (pada kapasitor). Beda potensial atau tegangan sumber pada rangkaian RLC AC seri memenuhi persamaan V = Vmax · sin (ωt + φ) dengan tegangan efektif memenuhi persamaan Vmax = Vef√2. Di mana tegangan sumber (V) tidak sama dengan penjumlahan tegangan dari ketiga komponen (V ≠ VR + VL + VC) melainkan dinyatakan seperti pada persamaan di atas.
Bagaimana bentuk rumus daya pada rangkaian RLC? Bagaimana cara hitung daya pada rangkaian RLC? Sobat idschool dapat mecari tahu jawabanya melalui ulasan di bawah.
Table of Contents
- Impedensi (Z) pada Rangkaian RLC Seri
- Rumus Daya pada Rangkaian AC RLC
- Rumus Frekuensi Resonansi (f0) Listrik
- Contoh Soal dan Pembahasan
Impedensi (Z) pada Rangkaian RLC Seri
Impedansi adalah sebutan untuk hambatan total pada rangkaian AC atau arus bolak-balik. Di mana, hubungan hambatan total (Z) sesuai Hukum Ohm pada arus searah yaitu perbandingan antara tegangan (V) dan arus (I).
Besar hambatan total pada rangkaian RLC AC atau impedansi (Z) memenuhi persamaan berikut.

Keterangan:
Z = impedansi (Ohm)
V = tegangan/beda potensial (Volt)
I = arus listrik (Ampere)
φ = beda fase
ω = kecepatan sudut (rad/s)
R = resistansi resistor (Ohm)
ZR = impedansi pada resistor (Ohm)
L = Induktor (Henry)
XL = reaktansi induktif (Ohm)
ZL = impedansi pada induktor (Ohm)
C = Kapasitor (Farad)
XC = reaktansi kapasitif (Ohm)
ZC = impedansi pada kapasitor (Ohm)
Perbandingan nilai XL (reaktansi induktif) dan XC (reaktansi kapasitif) dapat digunakan untuk menunjukkan sifat rangkaian. Ada tiga sifat rangkaian yang dapat terjadi yaitu bersifat induktif, kapasitif, atau beresonansi. Di mana, ketiga sifat rangkaian sesuai dengan ketentuan-ketentuan berikut.
- XL > XC: rangkaian bersifat induktif
- XL < XC: rangkaian bersifat kapasitif
- XL = XC: rangkaian beresonansi (bersifat resistif)
Baca Juga: 2 Contoh Cara Menghitung Biaya Pemakaian Listrik
Rumus Daya pada Rangkaian AC RLC
Besaran-besaran dalam arus bolak-balik atau fasor (phasor: phase vector) tegangan dan arus pada rangkaian arus searah (DC) memiliki fase sama sehingga cos φ = 1. Dengan demikian rumus daya pada arus searah (DC) memenuhi persamaan P = VI · cos φ = VI.
Sedangkan tegangan dan arus pada rangkaian AC RLC seri secara umum memiliki beda fase P. Sehingga, daya rata-rata yang diserap pada rangkaian RCL seri dengan arus AC sesuai persamaan P = V I · cos φ. Di mana, besaran cos φ ( pf ) disebut faktor daya yang sama dengan perbandingan VR atau R dengan impedansi (Z).

Baca Juga: Rumus Cepat Rambat Gelombang (v) dan Panjangnya (λ) dari Persamaan Gelombang Berjalan
Rumus Frekuensi Resonansi (f0) Listrik
Rangkaian AC akan bersenonsi ketika hambatan induktif (XL) sama dengan hambatan kapasitif (XC) sehingga impedansi rangkaian Z = R (minimum). Kondisi yang terjadi demikian menyebabkan arus listrik dan daya pada rangkaian menjadi bernilai maksimum. Peristiwa seperti ini dimanfaatkan dalam
Pada saat terjadi resonansi, frekuensi tegangan atau arus disebut dengan frekuensi resonansi yaitu saat ωL = 1/ωC. Rangkaian elektronik yang digunakan untuk membangkitkan frekuensi resonansi disebut osilator, seperti yang terdapat pada radio dan televisi. Persamaan untuk menghitung frekuensi resonansi sesuai dengan rumus berikut.

Baca Juga: Cara Hitung Beda Potensial (Tegangan) Antara Titik A dan B
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh oal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Rangkaian RLC Seri dengan Arus AC
Hambatan R, induktor L, dan kapasitor C masing-masing mempunyai nilai 300 ohm; 0,9 henry, dan 2 μF. Jika ketiga komponen listrik tersebut dihubungkan seri dan diberi tegangan efektif AC 50 volt, sedangkan frekuensi sudut AC 1.000 rad/s,
1) impedansi rangkaian 500 ohm;
2) arus efektif rangkaian 0,1 A;
3) tegangan yang melintasi L adalah 90 V;
4) tegangan yang melintasi C adalah 50 V.
Pernyataan yang benar adalah ….
A. 1), 2), dan 3)
B. 1) dan 3)
C. 2) dan 4)
D. hanya 4)
E. 1) 2), 3), dan 4)
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa informasi nilai seperti berikut.
- Hambata: R = 300 Ω
- Induktor: L = 0,9 H
- Kapasitor: C = 2 μF = 2×10‒6 F
- Tegangan efektif: Vef = 50 volt
- Frekuensi sudut: ω = 1.000 rad/s,
Menghitung impedansi (Z) rangkaian:
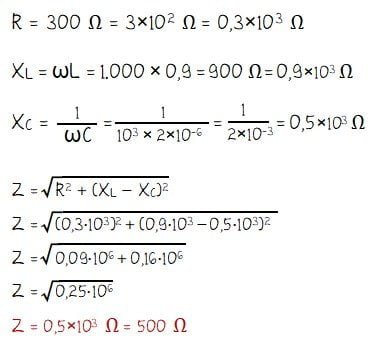
Menghitung arus efektif (Ief):
Ief = Vef/Z
Ief = 50/500 = 0,1 A
Tegangan yang melintasi L:
VL = Ief × XL
VL = 0,1 × 900 = 90 volt
Tegangan yang melintasi C:
VC = Ief × XC
VC = 0,1 × 500 = 50 volt
Jadi, pernyataan yang benar adalah 1), 2), 3), dan 4).
Jawaban: E
Contoh 2 – Soal Rangkaian RLC

Grafik gelombang sinus yang dihasilkan jika XL > XC sesuai rangkaian RLC seperti gambar di atas adalah ….
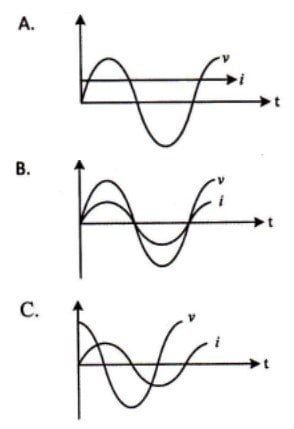

Pembahasan:
Rangkaian RLC yang memiliki nilai XL > XC bersifat induktif yang terjadi saat sudut fase positif. Di mana pada saat sudut fase positif yang terjadi adalah tegangan (v) mendahului arus (i). Sehingga gambar gelombang sinus yang dihasilkan sesuai pada pilihan C.
Jawaban: C
Baca Juga: Cara Membaca Hasil Pengukuran dengan Amperemeter dan Voltmeter
Contoh 3 – Soal Rangkaian RLC
Rangkaian RLC seri dengan R = 200 ohm, XL = 150 ohm, dan XC = 300 ohm dihubungkan dengan generator yang membangkitkan tegangan V = 120√2 sin 100πt volt dengan t dalam sekon. Daya yang diserap rangkaian adalah ….
A. 46 W
B. 40 W
C. 34 W
D. 23 W
E. 18 W
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh beberapa informsi seperti berikut.
- Hambatan: R = 200 ohm
- Reaktansi induktif: XL = 150 ohm
- Reaktansi kapasitif: XC = 300 ohm
- Tegangan maks: Vmax = 120√2 volt
Tegangan efektif: Vef = Vmax/√2
Vef = 120√2/√2 = 120 volt
Menghitung impedansi (Z):

Menentukan besar faktor daya (pf):
pf = R/Z
pf = 200/250 = 4/5 = 0,8
Menghitung daya yang diserap rangkaian:
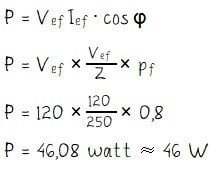
Jadi, daya yang diserap rangkaian adalah 46 W.
Jawaban: A
Contoh 4 – Daya pada Rangkaian RLC Seri
Rangkaian seri RLC dengan nilai R = 30 ohm, L = 40 mH, dan C = 50 μF dihubungkan pada sumber listrik. Rangkaian ini akan beresonandi pada frekuensi .…
A. 10/π√10 Hz
B. 250/π√2 Hz
C. 40√10 Hz
D. 2.500/π√10 Hz
E. 1.000 Hz
Pembahasan:
Cara menghitung frekuensi resonansi (f0) pada rangkaian RLC seri dengan nilai R = 30 ohm, L = 40 mH = 4×10-2 H, dan C = 50 μF = 5×10-5 F sesuai dengan cara penyelesaian berikut.

Jadi, rangkaian RCL seri akan beresonandi pada frekuensi 250/π√2 Hz.
Jawaban: B
Demikianlah tadi ulasan bentuk rangkaian RLC yaitu sebuah rangkaian listrik yang memuat tiga komponen yaitu resistor (R), induktor (L), dan kapasitor (C). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
muBaca Juga: Percoaan untuk Mencari Hubungan Antara Kuat Arus dan Beda Potensial
