Sistem Katrol pada Bidang Datar – Pembahasan materi sistem katrol bidang datar merupakan salah satu ilmu yang menerapkan Hukum Newton di dalamnya. Persamaan-persamaan yang diperoleh pada sistem katrol bidang datar berawal dari Hukum Newton, baik Hukum Newton I, II, atau III. Objek yang terlibat pada sistem katrol pada bidang datar adalah dua benda yang terhubung oleh tali dan melalui sebuah katrol.
Diketahui dua buah benda masing – masing terletak dalam sebuah sistem katrol pada bidang datar. Sistem pertama, benda diletakkan pada benda datar dengan permukaan licin. Sistem kedua, benda diletakkan pada benda datar dengan permukaan kasar. Apakah ada perbedaan persamaan pada kedua sistem katrol pada bidang datar tersebut? Tentu ada.
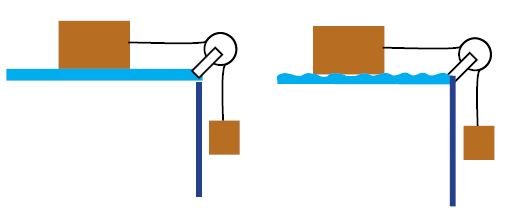
Pembahasan sistem katrol pada bidang datar akan dikelompokkan menjadi dua pembahasan. Pertama, pembahasan sistem katrol pada bidang datar licin. Dalam pembahasan ini, menganggap bahwa benda yang terletak pada bidang datar tidak mengalami gaya gesek.
Selanjutnya untuk pembahasan kedua adalah sistem katrol pada bidang datar kasar. Di sini, permukaan bidang datar yang menjadi tempat objek memiliki permukaan yang kasar, sehingga gaya gesek perlu dipertimbangkan.
Table of Contents
- Sistem Katrol pada Bidang Datar Licin
- Sistem Katrol pada Bidang Datar Kasar
- Contoh Soal dan Pembahasan
Sistem Katrol pada Bidang Datar Licin
Ulasan sistem katrol pada bidang datar licin akan dibagi lagi ke dalam dua pembahasan. Pembagian pembahasan didasarkan pada massa katrol. Akan dilihat bagaimana pengaruh massa katrol pada suatu sistem pertidaksamaan katrol.
Massa Katrol Diabaikan
Untuk bahasan pertama, sistem katrol yang akan diulas adalah sistem katrol pada bidang datar licin dan tidak memperdulikan massa katrol (mengabaikan massa katrol). Sistem katrol digambarkan seperti gambar di bawah.
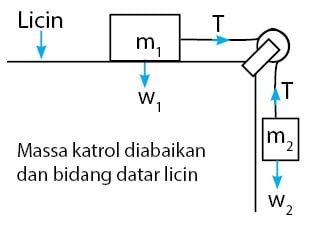
Hubungan persamaan yang dapat diperoleh melalui sistem katrol seperti gambar di atas dinyatakan melalui persamaan percepatan sistem katrol seperti berikut.

Keterangan:
a = percepatan gravitasi (m/s2)
w2 = berat benda kedua (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
Dari mana persamaan di atas diperoleh?
Berikut ini adalah langkah-langkah untuk mendapatkan persamaan percepatan pada sistem katrol bidang datar licin untuk massa katrol diabaikan.
Perhatikan kembali detail gaya seperti yang diperlihatkan pada gambar di atas.
Tinjau Benda 1:
∑F = m • a
T = m1 • a
Tinjau Benda 2:
∑F = m • a
w2 – T = m2 • a
T = w2 – m2 • a
Karena tegangan tali sama besar, maka:
m1 × a = w2 ‒ m2 × a
m1 × a + m2 × a = w2
a(m1 + m2) = w2
a = w2/m1 + m2
Diperoleh rumus percepatan sistem katrol seperti yang telah diberikan sebelumnya. Selanjutya akan dilihat pengaruh massa katrol pada persamaan percepatan sistem katrol.
Massa Katrol Tidak Diabaikan
Untuk melihat pengaruh massa katrol pada persamaan, sekarang akan dipertimbangkan massa katrol. Misalkan katrol yang terpasang pada sistem tersebut memiliki massa mk. Gambarnya dapat dilihat seperti berikut.
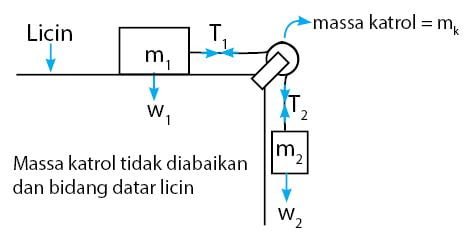
Hasil penurunan rumus untuk persamaan percepatan sistem katrol yang diperoleh seperti berikut ini.
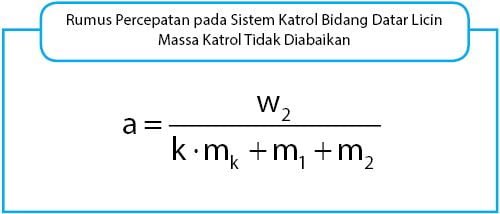
Keterangan:
a = percepatan gravitasi (m/s2)
k = bilangan/konstanta pada rumus inersia katrol
w2 = berat benda kedua (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
mk = massa katrol (kg)
Langkah-langkah penurunan rumusnya adalah sebagai berikut.
Tinjau Benda 1:
∑F = m • a
T1 = m1 • a
Tinjau Benda II:
∑F = m • a
w2 – T2 = m2 • a
T2 = w2 – m2 • a
Tinjau Katrol:
τ = l × α
T2 × r ‒ T1 × r = k × mk × r2 × a/r
(T2 ‒ T1)r = k × mk × r × a
T2 ‒ T1 = k × mk × a
Substitusi nilai T1 dan T2 ke persamaan katrol:
w2 ‒ m2 × a ‒ m1 × a = k × mk × a
w2 = k × mk × a + m2 × a + m1 × a
w2 = a(k × mk + m2 + m1)
a = w2/k × mk + m2 + m1
Terlihat bahwa massa katrol mempengaruhi besarnya percepatan. Semakin berat massa katrol, percepatan akan menjadi kecil. Kesimpulannya, semakin besar massa katrol akan membuat percepatan pada sistem katrol tersebut semakin kecil. Hal ini bisa dilihat dari nilai pembaginya yang semakin besar.
Lalu bagaimana pengaruh gaya gesek pada bidang datar? Sobat idschool dapat menyimak ulasannya pada materi sistem katrol pada bidang datar kasar yang diberikan di bawah.
Sistem Katrol pada Bidang Datar Kasar
Sama seperti sistem katrol bidang datar licin/halus, untuk sistem katrol pada bidang datar kasar akan dibagi menjadi dua kelompok. Pembagian kelompok juga didasarkan dengan mengabaikan atau tidak mengabaikan massa katrol.
Massa Katrol Diabaikan
Dua buah benda terhubung oleh sebuah tali dan katrol membentuk sebuah sistem katrol pada bidang datar. Sebuah benda terletak pada bidang datar kasar. Sedangkan benda satunyna tergantung. Gambar sistem katrol digambarkan seperti gambar di bawah.
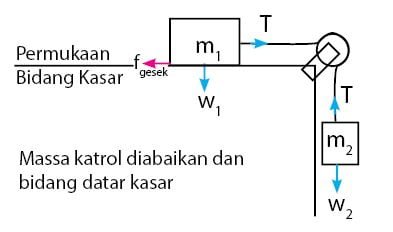
Hubungan rumus percepatan sistem katrol pada bidang datar seperti gambar di atas dinyatakan melaui persamaan di bawah.

Keterangan:
a = percepatan gravitasi (m/s2)
fg = gaya gesek antara benda 1 dan bidang kasar (N)
w2 = berat benda kedua (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
Langkah – langkah menurunkan rumus di atas adalah sebagai berikut. Sebelumnya perhatikan kembali detail gaya-gaya yang bekerja pada sistem katrol bidang datar kasar yang diberikan di atas.
Tinjau Benda 1:
∑F = m • a
T – fg = m1 • a
T = m1 • a + fg
Tinjau Benda 2:
∑F = m • a
w2 – T = m2 • a
T = w2 – m2 • a
Nilai tegangan tali T sama, sehingga akan akan diperoleh persamaan berikut.
m1 × a + fg = w2 ‒ m2 × a
m1 × a + m2 × a = w2 ‒ fg
a(m1 + m2) = w2 ‒ fg
a = w2 ‒ fg/m1 + m2
Terlihat bahwa gaya gesek akan membuat laju percepatan sistem katrol bidang datar menjadi lebih kecil. Berikutnya akan diulas bagaimana pengaruh massa katrol terhadap sistem.
Massa Katrol Tidak Diabaikan
Untuk melihat pengaruh massa katrol pada persamaan, sekarang akan dipertimbangkan massa katrol. Misalkan katrol yang terpasang pada sistem tersebut memiliki massa mk. Gambarnya dapat dilihat seperti berikut.
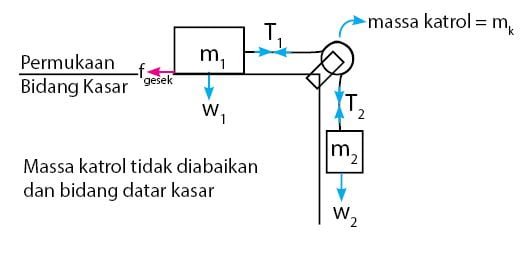
Hubungan rumus percepatan pada sistem katrol di atas adalah sebagai berikut.

Keterangan:
a = percepatan gravitasi (m/s2)
k = bilangan/konstanta pada rumus inersia katrol
fg = gaya gesek antara benda 1 dan bidang kasar (N)
w2 = berat benda kedua (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
mk = massa katrol (kg)
Langkah-langkah penurunan rumus percepatan sistem katrol pada bidang datar kasar untuk massa katrol tidak diabaikan.
Tinjau Benda 1:
∑F = m • a
T1 – fg = m1 • a
T1 = m1 • a + fg
Tinjau Benda 2:
∑F = m • a
w2 – T2 = m2 • a
T2 = w2 – m2 • a
Tinjau Katrol:
τ = l × α
T2 × r ‒ T1 × r = k × mk × r2 × a/r
(T2 ‒ T1)r = k × mk × r × a
T2 ‒ T1 = k × mk × a
Substitusi nilai T1 dan T2 ke persamaan pada katrol:
w2 ‒ m2 × a ‒ (m1 × a + fg) = k × mk × a
w2 ‒ m2 × a ‒ m1 × a ‒ fg = k × mk × a
w2 ‒ fg = k × mk × a + m2 × a + m1 × a
w2 ‒ fg = a(k × mk + m2 + m1)
a = w2 ‒ fg/k × mk + m2 + m1
Demikianlah uraian penurunan rumus percepatan sistem katrol pada bidang datar untuk massa katrol tidak diabaikan. Massa katrol akan membuat laju percepatan berubah. Semakin besar massa katrol yang digunakan, semakin kecil laju percepatan sistem katrol yang dihasilkan.
Perhatikan contoh soal sistem katrol pada bidang datar berikut, untuk menambah pemahaman sobat idschool.
Baca Juga:
- Sistem Katrol dan Bidang Miring
- Sistem Katrol Majemuk
- Katrol Begerak: Persamaan Tegangan Tali dan Percepatan
Contoh Soal dan Pembahasan
Perhatikan gambar di bawah!
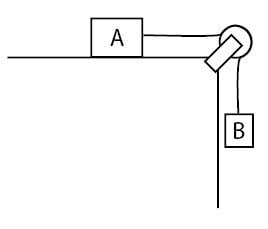
Balok A diletakkan di atas meja kemudian diikat tali yang menghubungkan balok B. Tali yang menghubungkan balok A dan B melalui sebuah katrol seperti yang diperlihatkan pada gambar sistem katrol di atas. Massa balok A dan balok B berturut-turut adalah 3 kg dan 2 kg.
Jika massa katrol diabaikan sedangkan gravitasi 10 m/s2 dan koefisien gesek kinetiknya adalah 0,4. Besar percepatan sistem katrol tersebut adalah ….
A. 0,4 m/s2
B. 0,8 m/s2
C. 1,6 m/s2
D. 2,4 m/s2
E. 3,2 m/s2
Pembahasan:
Gaya-gaya yang bekerja pada sistem katrol pada soal yang diberikan dapat dilihat seperti gambar di bawah.
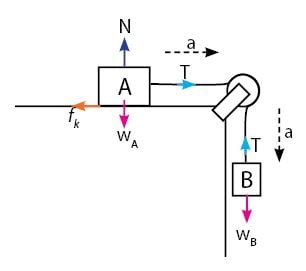
Mencari besar gaya Normal pada benda A:
gaya normal (N) pada benda A sama dengan wA karena terletak pada bidang datar.
N = wA
N = mA × g
N = 3 × 10 = 10 N
Untuk menghitung nilai percepatan, kita tidak perlu lagi menurunkan rumus perceptan. Ambil persamaan percepatan sistem katrol yang sesuai dengan kondisi pada soal yang diberikan. Seperti rumus percepatan sistem katrol pada bidang datar berikut (bidang datar kasar dan massa katrol diabaikan).
Mencari percepatan gerak benda:
a = w2 ‒ fg/m2 + m1
a = m2 × g ‒ μk × N/m2 + m1
a = 2 × 10 ‒ 0,4 × 30/2 + 3
a = 20 ‒ 12/5
a = 8/5 = 1,6 m/s2
Jadi, balok A bergerak ke kanan dan balok B bergerak ke bawah dengan percepatan 1,6 m/s2.
Jawaban: C
Sekian tadi ulasan tentang sistem katrol pada bidang datar, meliputi sistem katrol pada bidang datar licin dan kasar. Serta melihat pengaruh massa katrol terhadap persamaan pada sistem katrol bidang datar. Terimakasih telah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Sistem Katrol Sederhana
