Katrol merupakan salah satu jenis pesawat sederhana yang dapat mempermudah pekerjaan manusia. Bahasan dalam sistem katrol sederhana memuat gaya-gaya apa saja yang bekerja pada katrol. Persamaan dalam sistem katrol sederahan merupakan contoh penerapan Hukum Newton pada bidang ilmu mekanika. Hukum Newton yang berlaku pada sistem setimbang adalah Hukum I Newton. Sedangkan Hukum Newton pada sistem katrol bergerak adalah Hukum II Newton.
Katrol adalah roda yang memiliki poros, biasanya di sekeliling roda terdapat lintasan sebagai tempat untuk tali. Sedangkan sistem katrol merupakan kumpulan sejumlah katrol, baik katrol tetap atau katrol bergerak.

Baca Juga: Besar Keuntungan Mekanis Katrol
Bagaimana bentuk persamaan pada sistem katrol sederhana? Apa saja faktor yang mempengauhi persamaan pada sistem karol? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Sistem Katrol Sederhana untuk Massa Katrol Diabaikan
- Sistem Katrol Sederhana untuk Massa Katrol Tidak Diabaikan
- Contoh Soal dan Pembahasan
Sistem Katrol Sederhana untuk Massa Katrol Diabaikan
Dua buah benda dengan massa berbeda terpasang pada seutas tali yang terhubung pada katrol. Perbedaan massa dari kedua benda membuat salah satu benda akan bergerak ke atas dan benda lainnya bergerak ke bawah. Pada sistem tersebut, terdapat gaya tengangan tali T yang menopang benda ke atas dan gaya berat masing-masing benda dengan arah menuju gravitasi bumi.
Gambaran sederhana sistem katrol dengan dua benda pada sebuah katrol diberikan seperti berikut.

Besar percepatan gerak benda pada sistem tersebut dengan mengabaikan massa katrol dan gaya gesek dapat dihitung dengan rumus beriku.

Keterangan:
a = percepatan sistem (m/s2)
w2 = berat benda kedua (N)
w1 = berat benda pertama (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
Bagaimana persamaan di atas diperoleh?
Seperti yang telah disinggung sedikit di atas bahwa persamaan tersebut diturunkan melaui Hukum Newton. Perhatikan langkah-langkahnya berikut ini.
Sebelumnya tinjau kembali benda 1 dan benda 2 pada gambar katrol sederhana yang diberikan di atas.
Tinjau Benda 1 (w1):
∑F = m • a
T – w1= m1 • a
T = m1 • a + w1
Tinjau Benda 2 (w2):
∑F = m • a
w2 – T = m2 • a
T = w2 – m2 • a
Karana tegangan tali sama besar, maka dapat diperoleh persamaan dan penyelesaiannya seperti langkah-langkah berikut.
m1 × a + w1 = w2 ‒ m2 × a
m1 × a + m2 × a = w2 ‒ w1
a(m1 + m2) = w2 ‒ w1
a = w2 ‒ w1/m1 + m2
Baca Juga: Gaya Gesek Statis dan Gaya Gesek Kinetis
Sistem Katrol Sederhana untuk Massa Katrol Tidak Diabaikan
Ulasan sebelumnya telah membahas persamaan yang berlaku pada sistem katrol sederhana untuk massa katrol yang diabaikan. Bagaimana pengaruh massa katrol pada suatu sistem katrol? Apakah persamaanya akan tetap? Atau berubah? Untuk melihat pengaruh massa katrol pada sistem katrol sederhana, perhatikan uraian berikut ini.
Perhatikan gambar di bawah!
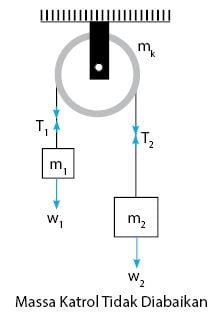
Di sini, massa katrol disimbolkan dengan mk. Ternyata massa katrol mempengaruhi persamaan percepatan pada sistem katrol sederhana, seperti terlihat pada persamaan di bawah.

Keterangan:
a = percepatan sistem (m/s2)
k = bilangan/konstanta pada rumus inersia katrol
w2 = berat benda kedua (N)
w1 = berat benda pertama (N)
m1 = massa benda pertama (kg)
m2 = massa benda kedua (kg)
mk = massa katrol (kg)
Berikut ini adalah langkah-langkah penurunan rumus percepatan pada sistem katrol sederhana tanpa mengabaikan massa katrol.
Tinjau Benda 1:
∑F = m • a
T1 – w1 = m1 • a
T1 = m1 • a + w1
Tinjau Benda 2:
∑F = m • a
w2 – T2 = m2 • a
T2 = w2 – m2 • a
Tinjau katrol:
∑F = l × a
T2 × r ‒ T1 × r = k × mk × r2 × a/r
(T2 ‒ T1)r = k × mk × r × a
T2 ‒ T1 = k × mk × a
Substitusi nilai T1 dan T2 ke persamaan katrol, sehingga diperoleh persamaan dan penyelesaiannya seperti langkah-langkah berikut.
T2 ‒ T1 = k × mk × a
w2 ‒ m2 × a ‒ (m1 × a + w1) = k × mk × a
w2 ‒ m2 × a ‒ m1 × a ‒ w1 = k × mk × a
w2 ‒ w1 ‒ m2 × a ‒ m1 × a = k × mk × a
w2 ‒ w1 = k × mk × a + m2 × a + m1 × a
w2 ‒ w1 = a(k × mk + m2 + m1)
a = w2 ‒ w1/k × mk + m2 + m1
Kesimpulannya, massa katrol akan mempengaruhi persamaan pada suatu sistem katrol sederhana.
Baca Juga:
Contoh Soal dan Pembahasan
Terdapat dua balok yang tergantung pada sebuah sistem katrol sederhana. Balok A dan B memiliki massa berturut-turut adalah 4 kg dan 6 kg. Sistem mula-mula diam, kemudian dilepaskan.
Apabila g = 10 m/s2 serta gaya gesek dan massa katrol diabaikan, maka percepatan pada sistem katrol tersebut adalah ….
A. 1 m/s2
B. 2 m/s2
C. 3 m/s2
D. 4 m/s2
E. 5 m/s2
Pembahasan:
Berdasarkan soal dapat diperoleh informasi-informasi sepeti berikut.
- ma = 4 kg
- mb = 6 kg g = 10 m/s2
- wa = ma × g = 4 × 10 = 40 N
- wb = mb × g = 6 × 10 = 60 N
Percepatan pada sistem katrol sederhana tersebut dapat dihitung seperti penyelesaiannya cara berikut. (gunakan rumus percepatan pada sistem katrol untuk massa katrol diabaikan)
Menghitung percepatan gerak benda:
a = wb ‒ wa/ma + mb
a = 60 ‒ 40/4 + 6
a = 20/10
a = 2 m/s2
Jadi, percepatan gerak benda pada sistem tersebut adalah a = 2 m/s2.
Jawaban: B
Demikianlah tadi ulasan tentang sistem katrol sederhana yang meliputi sistem dengan massa katrol diabaikan dan sistem dengan memperhatikan massa katrol. Terimakasih sudah mengunjungi idscool(dot)net, semoga bermanfaat.
Baca Juga: Katrol Bergerak ~ Persamaan Tegangan Tali dan Percepatan
