Sistem Katrol Bidang Miring

Sistem katrol bidang miring adalah sebuah sistem yang di dalamnya terdapat katrol dan bidang miring. Bahasan dalam sistem katrol bidang miring adalah melihat gaya apa yang bekerja pada benda. Dengan mengetahui gaya-gaya yang bekerja pada benda, nantinya percepatan gerak benda dapat ditentukan/dihitung.

Sebuah sistem katrol bidang miring melibatkan obyek/benda yang terletak pada bidang miring, sebuah katrol, dan sebuah benda yang tergantung pada tali yang terhubung dengan benda lainnya melalui katrol. Gambaran sistem katrol bidang miring adalah benda di atas bidang miring yang terikat oleh tali dan terhubung pada katrol diberikan seperti berikut.

Bahasan pada sistem katrol bidang miring meliputi 4 macam:
Pertama adalah melihat persamaan pada sistem katrol pada bidang miring dengan massa katrol diabaikan dan bidang permukaan licin. Kedua adalah sistem katrol pada bidang miring dengan mempertimbangkan massa katrol (massa katrol diketahui) dan bidang licin.

Ketiga, pembahasan mempertimbangkan pengaruh gaya gesek, melihat persamaan pada sistem katrol pada bidang miring kasar dengan mengabaikan massa katrol. Dan yang terakhir atau keempat, pembahasan persamaan sistem katrol pada bidang miring kasar dengan mempertimbangkan massa katrol (massa katrol diketahui).

Table of Contents

• Massa Katrol Diabaikan dan Bidang Licin
• Massa Katrol Tidak Diabaikan (Diketahui) dan Bidang Licin
• Massa Katrol Diabaikan dan Bidang Kasar
• Massa Katrol Tidak Diabaikan (Diketahui) dan Bidang Kasar
• CONTOH SOAL DAN PEMBAHASAN

Massa Katrol Diabaikan dan Bidang Licin

Bahasan pertama adalah melihat bagaimana persamaan dan gaya-gaya yang bekerja pada sistem katrol bidang miring dengan mengabaikan massa katrol dan gaya gesek. Kondisi bidang miring di sini memiliki permukaan licin sehingga gaya gesek dapat diabaikan. Selain itu, asumsi yang digunakan pada sistem katrol bidang miring di sini juga akan mengabaikan pengaruh massa katrol dalam sistem.

Gambaran sistem katrol bidang miring dengan massa katrol dan gaya gesek diabaikan terlihat seperti berikut.

Persamaan yang berlaku untuk model sistem katrol seperti di atas adalah seperti berikut.

 
Keterangan:
a = percepatan sistem (m/s²)
w₁ = berat benda pertama (N)
w₂ = berat benda kedua (N)

m₁ = massa benda pertama (kg)
m₂ = massa benda kedua (kg)
θ = sudut kemiringan bidang (^o)

Persamaan di atas dapat digunakan untuk menghitung percepatan sistem katrol yang sesuai dengan kondisi massa katrol diabaikan dan bidang miring licin, sehingga tidak ada gaya gesek (gaya gesek diabaikan).

Rumus di atas diturunkan dengan berdasarkan Hukum Newton dan prinsip gaya pada bidang miring. Langkah-langkah mendapatkan rumus percepatan sistem katrol pada bidang miring seperti yang telah diberikan di atas dapat di simak seperti berikut ini.

Perhatikan kembali gambar sistem katrol yang diberikan di atas. Perhatikan detail gaya-gaya yang bekerja pada sitem tersebut.

Tinjau Benda 1:
∑F = m • a
T₁ – w_1x = m₁ • a
T₁ = m₁ • a + w_1x
T = m₁ • a + w_1x
T = m₁ • a + w₁ • sin θ

Tinjau Benda 2:
∑F = m • a
w₂ – T₂ = m₂ • a
T₂ = w₂ – m₂ • a
T = w₂ – m₂ • a

Karena tegangan tali sama besar, T = T maka diperoleh persamaan seperti di bawah.

m₁ × a + w₁ sinθ= w₂ ‒ m₂ × a
m₁ × a + m₂ × a = w₂ ‒ w₁ sin θ
a(m₁ + m₂) = w₂ ‒ w₁ sinθ
a = ^{w2 ‒ w1 sin θ}/_{m1 + m2}

Sesuai dengan rumus percepatan yang diberikan di awal. Berikutnya, akan diulas sistem katrol dengan model sejenis model pertama ini, hanya saja kita akan lihat pengaruh massa katrol pada persamaan.

Baca Juga:

• Sistem Katrol Sederhana
• Sistem Katrol Majemuk

Massa Katrol Tidak Diabaikan (Diketahui) dan Bidang Licin

Diberikan sebuah sistem katrol yang sama dengan model sebelumnya, namun pada permasalahan sistem katrol bidang miring yang ke dua ini dilakukan dengan melihat pengaruh massa katrol. Bagaimanakah pengaruh massa katrol terhadap persamaan-persamaan pada sistem katrol bidang miring?

Sebelumnya perhatikan sistem katrol bidang miring licin dan massa katrol diketahui sebesar m_k berikut ini.

Catatan penting untuk sistem katrol di atas adalah tegangan tali tidak sama (T₁ ≠ T₂) dan tidak ada gaya gesek. Persamaan yang berlaku untuk sistem katrol bidang miring licin dan massa katrol m_k adalah seperti berikut.

Keterangan:
a = percepatan sistem (m/s²)
k = bilangan/konstanta pada rumus inersia katrol
w₁ = berat benda pertama (N)
w₂ = berat benda kedua (N)

m₁ = massa benda pertama (kg)
m₂ = massa benda kedua (kg)
m_k = massa katrol (kg)
θ = sudut kemiringan bidang (^o)

Cara mendapatkan rumus percepatan pada sistem katrol untuk bidang miring licin dan diketahui massa katrol m_k dapat disimak melalui langkah-langkah berikut.

Tinjau Benda 1:
∑F = m • a
T₁ – w_1x = m₁ • a
T₁ = m₁ • a + w_1x
T₁ = m₁ • a + w_1x
T₁ = m₁ • a + w_{1 •} sin θ

Tinjau Benda 2:
∑F = m • a
w₂ – T₂ = m₂ • a
T₂ = w₂ – m₂ • a

Tinjau Katrol:
∑τ = l × α
T₂ × r ‒ T₁ × r = k × m_k × r² × ^a/_r
r(T₂ ‒ T₁) = k × m_k × r × a
T₂ ‒ T₁ = k × m_k × a

Substitusi nilai T₁ dan T₂ ke persamaan katrol, maka akan diperoleh persamaan dan penyelesaiannya seperti berikut.

T₂ ‒ T₁ = k × m_k × a
w₂ ‒ m₂ × a ‒ (m₁ × a + w₁ × sin θ) = k × m_k × a
w₂ ‒ m₂ × a ‒ m₁ × a ‒ w₁ × sin θ = k × m_k × a
w₂ ‒ w₁ × sin θ = k × m_k × a + m₂ × a + m₁ × a
w₂ ‒ w₁ × sin θ = a(k × m_k + m₂ + m₁)
a = ^{w2 ‒ w1 × sin θ}/_{k × mk + m2 + m1}

Diperoleh persamaan percepatan sistem katrol pada bidang miring licin dan massa katrol m_k. Untuk dua pembahasan berikutnya, akan dilihat pengaruh gaya gesek pada persamaan – persamaan dalam sistem katrol.

Baca Juga: Persamaan Tegangan Tali dan Percepatan pada Katrol Bergerak

Massa Katrol Diabaikan dan Bidang Kasar

Model sistem katrol bidang miring yang ketiga, tidak jauh berbeda dengan dua model sebelumnya. Perbedaan terletak pada permukaan bidang miring. Kedua model pembahasan sebelumnya, permukaan bidang yang digunakan licin. Sehingga tidak ada gaya gesek, atau lebih tepatnya mengabaikan gaya gesek. Berikutnya akan diulas untuk permukaan bidang miring kasar, sehingga gaya gesek perlu dipertimbangkan.

Ingat bahwa pada bahasan ini, massa katrol pada diabaikan.
Catatan penting untuk sistem katrol jenis ini adalah tegangan tali sama T₁ = T₂ = T dan tedapat gaya gesek. Gambaran sistem katrol bidang miring kasar beserta gaya-gaya yang bekerja pada benda diberikan seperti berikut.

Persamaan yang akan diperoleh diberikan seperti berikut ini.

Keterangan:
a = percepatan sistem (m/s²)
f_g = gaya gesek (N)
w₁ = berat benda pertama (N)
w₂ = berat benda kedua (N)

m₁ = massa benda pertama (kg)
m₂ = massa benda kedua (kg)
θ = sudut kemiringan bidang (^o)

Langkah – langkah mendapatkan persamaan percepatan sistem katrol pada bidang miring kasar dan massa katrol diabaikan.

Perhatikan kembali detail gaya-gaya yang bekerja pada sistem katrol seperti gambar di atas.

Tinjau Benda 1:
∑F = m • a
T₁ – w_1x – f_g = m₁ • a
T₁ = m₁ • a + f_g + w_1x
T = m₁ • a + f_g + w_1x
T = m₁ • a + f_g + w₁ • sin θ

Tinjau Benda 2:
∑F = m • a
w₂ – T₂ = m₂ • a
T₂ = w₂ – m₂ • a
T = w₂ –  m₂ • a

Karena tegangan tali sama besar, T = T maka diperoleh persamaan dan penyelesaiannya seperti cara di bawah.

m₁ × a + f_g + w₁ sin θ = w₂ ‒ m₂ × a
m₁ × a + m₂ × a = w₂ ‒ f_g ‒ w₁ sin θ
a(m₁ + m₂) = w₂ ‒ f_g ‒ w₁ sin θ
a = ^{w2 ‒ fg ‒ w1 × sin θ}/_{m1 + m2}

Baca Juga: Keuntungan Mekanis Katrol

Massa Katrol Tidak Diabaikan (Diketahui) dan Bidang Kasar

Pembahasan berikutnya, akan dilihat pengaruh massa katrol pada persamaan sistem katrol bidang miring kasar.

Di sini, kita akan melihat pengaruh massa katrol untuk model sistem katrol bidang miring dengan permukaan kasar. Catatannya adalah tegangan tali tidak sama T₁ =  T₂ dan terdapat gaya gesek. Gambar sistemnya adalah seperti berikut.

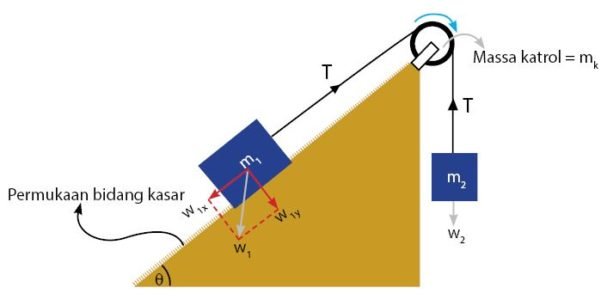
Persamaan percepatan yang diperoleh adalah sebagai berikut.

Keterangan:
a = percepatan sistem (m/s²)
k = bilangan/konstanta pada rumus inersia katrol
f_g = gaya gesek (N)

w₁ = berat benda pertama (N)
w₂ = berat benda kedua (N)
m₁ = massa benda pertama (kg)
m₂ = massa benda kedua (kg)

m_k = massa katrol (kg)
θ = sudut kemiringan bidang (^o)

Langkah – langkah mendapat persamaan di atas adalah seperti berikut ini.

Tinjau Benda 1:
∑F = m • a
T₁ – w_1x – f_g = m₁ • a
T₁ = m₁ • a + f_g + w_1x
T₁ = m₁ • a + f_g + w_1x
T₁ = m₁ • a + f_g + w₁ • sin θ

Tinjau Benda 2:
∑F = m • a
w₂ – T₂ = m₂ • a
T₂ = w₂ – m₂ • a

Tinjau Katrol:
∑τ = l × α
T₂ × r ‒ T₁ × r = k × m_k × r² × ^a/_r
r(T₂ ‒ T₁) = k × m_k × r × a
T₂ ‒ T₁ = k × m_k × a

Substitusi nilai T₁ dan T₂ ke persamaan katrol, maka akan diperoleh persamaan dan penyelesaiannya seperti berikut.

T₂ ‒ T₁ = k × m_k × a
w₂ ‒ m₂ × a ‒ (m₁ × a + f_g + w₁ × sin θ) = k × m_k × a
w₂ ‒ m₂ × a ‒ m₁ × a ‒ f_g ‒ w₁ × sin θ = k × m_k × a
w₂ ‒ f_g ‒ w₁ × sin θ = k × m_k × a + m₂ × a + m₁ × a
w₂ ‒ f_g ‒ w₁ × sin θ = a(k × m_k + m₂ + m₁)
a = ^{w2 ‒ fg ‒ w1 \cdot sin \; \theta}/ _{k × mk + m2 + m1}

Baca Juga: Sistem Katrol pada Bidang Datar

CONTOH SOAL DAN PEMBAHASAN

Perhatikan bidang miring kasar seperti yang terlihat pada gambar di bawah!

Balok yang terletak pada bidang miring memiliki massa 2 kg. Sebuah balok yang lain tergantung pada tali dengan massa 5 kg. Koefisien gesekan kinetis antara bidang miring dengan benda 1 adalah 0,2.

Percepatan pada sistem katrol di atas adalah …. (sin 37^o = 0,6; cos 37^o= 0,8; g = 10 m/s²)
A. 4,79 m/s²
B. 4,97 m/s²
C. 5,07 m/s²
D. 5,79 m/s²
E. 5,97 m/s²

Pembahasan:
Uraian gaya yang sesuai pada keterangan yang diberikan pada soal sesuai dengan gambar berikut.

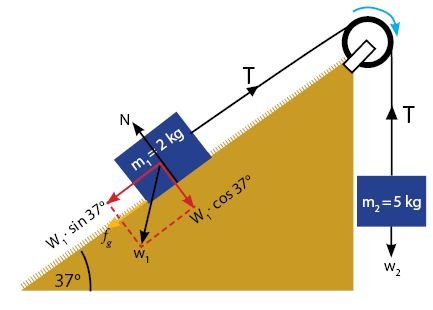
Untuk mendapatkan percepatan pada sistem katrol di atas, sobat idschool tidak perlu menurunkan kembali rumusnya. Gunakan rumus percepatan yang telah diperoleh di atas, sesuai dengan kondisi pada soal yang diberikan.

Menghitung percepatan berikut (massa katrol diabaikan dan permukaan bidang miring kasar):

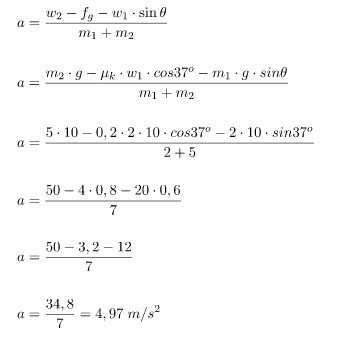
Jadi, besar percepatan pada sistem katrol pada soal adalah 4,97 m/s².

Jawaban: B

Demikianlah ulasan tentang sistem katrol bidang miring yang meliputi empat bahasan yaitu sistem katrol bidang miring licin dan mengabaikan massa katrol, sistem katrol pada bidang miring licin dengan massa katrol, sistem katrol bidang miring kasar dan mengabaikan massa katrol, serta sistem katrol bidang miring kasar dengan massa katrol. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Gaya Gesek ~ Pengertian, Rumus, dan Contoh Soal