Gradien Garis Lurus yang Saling Sejajar dan Tegak Lurus

Sifat gradien garis lurus yang saling sejajar adalah memiliki nilai yang sama. Sedangkan sifat gradien garis lurus yang saling tegak lurus adalah nilainya merupakan lawan kebalikannya.

Contohnya garis lurus y = 3x + 5 dengan garis lurus 3x – y + 8 = 0 akan saling sejajar. Sedangkan garis lurus y = 3x + 5 dengan garis lurus x + 3y + 8 = 0 akan saling tegak lurus.

Ulasan lebih banyak mengenai gradien garis lurus yang saling sejajar dan tegak lurus ada di bawah.

Daftar isi:

• Gradien Garis Lurus yang Sejajar
• Gradien Garis Lurus yang Tegak Lurus
• Contoh Soal dan Pembahasan
  • Contoh 1
  • Contoh 2
  • Contoh 3

Gradien Garis Lurus yang Sejajar

Dua buah garis sejajar memiliki nilai gradien yang sama. Misalkan diketahui garis g sejejar dengan garis h. Kedua garis tersebut memiliki kemiringan yang dinyatakan dalam nilai gradien. Besar nilai gradien garis g dan garis h adalah sama dengan.

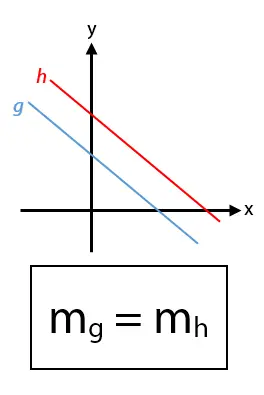
Untuk nilai gradien garis g adalah m_g dan nilai gradien garis h adalah m_h. Hubungan yang menyetakan sifat gradien garis lurus yang sejajar adalah m_g = m_h.

Contoh:
Gradien garis lurus yang sejajar dengan garis 6x – 2y + 8 = 0 adalah ….

Jawab:
Gradien garis lurus yang akan dicari sama dengan gradien garis 6x – 2y + 8 = 0 karena keduanya diketahui sejajar. Sehingga untuk menyelesaikan soal di atas hanya perlu mencari nilai gradien garis 6x – 2y + 8 = 0.

Mencari gradien garis 6x – 2y + 8 = 0:

Jadi, gradien garis lurus yang sejajar dengan garis 6x – 2y + 8 = 0 adalah m = 3.

Baca Juga: Persamaan Garis Lurus yang Saling Sejajar

Gradien Garis Lurus yang Tegak Lurus

Hubungan nilai gradien dari dua garis yang saling tegak lurus adalah lawan kebalikan dari gradien-gradiennya. Atau dapat juga dinyatakan dalam persamaan bahwa hasil kali gradien garis yang saling tegak lurus adalah –1.

Misalkan diketahui dua buah garis yaitu garis g dan garis h. Kedua garis tersebut saling tegak lurus. Gradien garis g adalah m_g dan gradien garis h adalah m_h. Hubungan nilai gradien antara garis g dan garis h adalah m_g × m_h = –1.

Contoh:
Perhatikan gambar berikut!

Gradien garis lurus yang tegak lurus dengan garis a adalah ….

Jawab:
Pertama perlu menentukan gradien garis a terlebih dahulu.

Gradien garis dari gambar dapat dihitung menggunakan tumus m = ^Δy/_Δx (untuk garis yang condong ke kanan) atau m = –^Δy /_Δx (untuk garis yang condong ke kiri).

Dari gambar dapat diketahui bahwa garis a condong ke kanan, Δy = 5, dan Δx = 3. Sehingga gradien garis a dapat dihitung dengan rumus m = ^Δy/_Δx.

Menghitung gradien garis a:

Selanjutnya dapat dicari gradien garis yang tegak lurus dengan garis a menggunakan sifat gradien kedua garis yang memenuhi hubungan m_a × m = –1.

Menentukan gradien garis lurus yang tegak lurus dengan garis a:

m_a × m = –1

⁵/₃ × m = –1

m = –1 : ⁵/₃

m = –1 × ³/₅ = –³/₅

Jadi, gradien garis lurus yang tegak lurus dengan garis a adalah m = –³/₅

Baca Juga: Rumus Persamaan Garis Lurus yang Diketahui Melalui 2 Titik

Contoh Soal dan Pembahasan

Pembahasan soal gradien garis lurus yang saling sejajar dan tegak lurus ada di bawah.

Contoh 1

Diketahui garis g melalui titik A(−11, 8) dan titik B(−3, 4). Garis l melalui titik P(−5, 12) dan Q(7, k). Jika garis g sejajar terhadap garis l, maka nilai k adalah ….
A.  2 
B.  4 
C.  6 
D.  8 

Pembahasan:
Pada soal diketahui bahwa garis g sejajar terhadap garis l. Dengan demikian dapat disimpulkan bahwa nilai gradien garis g sama dengan nilai gradien garis l.

Diketahui dua titik yang melalui,

• Garis g → A(−11, 8) dan B(−3, 4)
• Garis l → P(−5, 12) dan Q(7, k)

Sehingga,

m_g = m_l

8(k – 12) = –4 × 12

8k – 96 = –48

8k = –48 + 96 = 48

k = ⁴⁸/₈ = 6

Jadi, nilai k adalah 6.

Jawab: C

Contoh 2

Perhatikan gambar di bawah!

Gradien garis l adalah ….
A. –2
B. –¹/₂
C. ¹/₂
D. 2

Pembahasan:
Pertama yang bisa dilakukan adalah menentukan gradien garis g karena dapat secara mudah mengetahui nilai Δx = 3 dan Δy = 6.

Dari gambar dapat diketahui bahwa garis condong ke kanan sehingga nilai gradiennya positif. Nilai gradien garis g adalah m_g = ^Δy /_Δx = ⁶/₃ = 2.

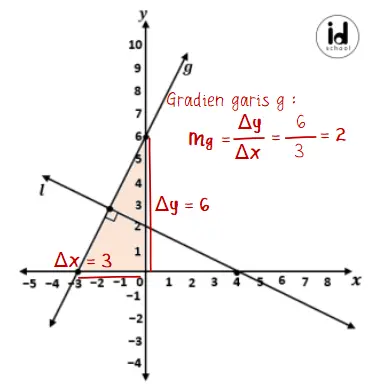
Dari gambar dapat diketahui bahwa garis g tegak lurus dengan garis l. Sehingga hubungan nilai antara kedua garis tersebut memenuhi persamaan m_g · m_l = –1.

Dengan sifat gradien garis lurus yang tegak lurus tersebut dapat dicari tahu nilai gradien garis l.

Mencari gradien garis l :

m_g · m_l = –1

2 × m_l = –1

Jadi, gradien garis l adalah m_l = –¹/₂.

Jawab: B

Contoh 3

Diketahui garis y = 2x – 1 dan 4x – 2y = 10. Kedudukan dua garis tersebut adalah ….
A. sejajar
B. berimpit
C. tegak lurus
D. berpotongan

Pembahasan:
Kedudukan dua garis dapat diketahui melalu nilai gradien.

• Gradien garis:
  • y = 2x – 1
    → m = 2
  • 4x – 2y = 10
    → m = –4/(–2) = 2

Garis y = 2x – 1 dan 4x – 2y = 10 memiliki gradien yang sama. Kedudukan garis dapat berimpit atau sejajar. Untuk melihatnya, bisa coba substitusi nilai x. Jika menghasilkan nilai y yang berbeda untuk satu nilai x, kedua garis tidak berimpit.

• Untuk x = 1
  • y = 2x – 1
    y = 2(1) – 1 = 1
  • 4x – 2y = 10
    4(1) – 2y = 10
    2y = 4 – 10
    2y = –6
    y = –6 : 2 = –3

Diperoleh nilai y yang berbeda untuk satu nilai x yang sama. Artinya, dua garis tersebut hanya sejajar, namun tidak berimpit.

Jadi, kedudukan dua garis tersebut adalah sejajar.

Jawaban: A

Demikianlah tadi ulasan sifat gradien garis lurus yang sejajar dan tegak lurus. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!