Perbandingan Segitiga Siku-Siku dengan Sudut Istimewa

Segitiga siku-siku adalah jenis segitiga yang memiliki karakteristik salah satu sudutnya sama dengan 90^o (besar sudut 90^o = sudut siku-siku). Dalam sebuah segitiga, ketiga sudutnya memiliki jumlah sama dengan 180^o. Sehingga jumlah dua buah buah sudut lainnya pada segitiga siku-siku adalah 90^o. Sudut 90^o bersama dengan sudut-sudut 30^o, 37^o, 45^o, 53^o, dan 60^o merupakan sudut istimewa.

Besar ketiga sudut dalam segitiga menentukan perbandingan perbandingan panjang sisi segitiga yang memiliki hubungan sebanding. Untuk perbandingan sisi segitiga siku-siku dengan sudut istimewa dapat dinyatakan dalam perbandingan bilangan real positif. Bagaimana perbandingan sisi segitiga siku-siku dengan istimewa? Sobat idshcool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Hubungan Panjang Ketiga Sisi Segitiga Siku-Siku
• Perbandingan Sisi Segitiga Siku-Siku dengan Sudut Istimewa 30o, 60o, dan 90o
• Perbandingan Sisi Segitiga Siku-Siku dengan Sudut Istimewa 45o, 45o, dan 90o
• Perbandingan Sisi Segitiga Siku-Siku dengan Sudut Istimewa 37o, 53o, dan 90o
• Contoh Penggunaan Rumus Perbandingan Sisi Segitiga Siku-Siku
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Perbandingan Sisi Segitiga Siku-Siku
  • Contoh 2 – Soal Perbandingan Sisi Segitiga Siku-Siku

Hubungan Panjang Ketiga Sisi Segitiga Siku-Siku

Pada sebuah segitiga siku – siku terdapat persamaan yang menyatakan hubungan antara panjang sisi – sisi segitiga. Hubungan tersebut dinyatakan dalam persamaan kuadrat sisi miring sama dengan jumlah kuadrat kedua sisinya. Pernyataan tersebut sesuai dengan sebuah teorema yang dikenal sebagai teorema Pythagoras.

Persamaan Pythagoras dapat digunakan untuk menghitung sisi miring segitiga jika kedua sisi lainnya diketahui. Misalnya AC merupakan sisi miring dari segitiga ABC dengan sudut siku-siku di titik B. Diketahui panjang sisi AB dan BC secara urut adalah 6 cm dan 8 cm. Perhitungan dengan teorema pthagoras akan menghasilkan panjang sisi AC untuk segitiga tersebut adalah 10 cm.

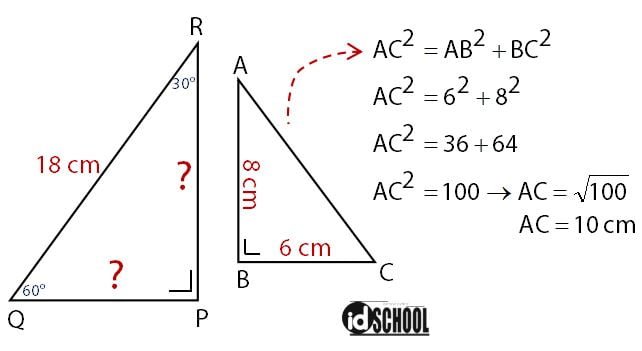
Jika yang diketahui hanya sisi miring dan ketiga sudut segitiga yaitu 30^o, 60^o, dan 90^o maka panjang dua sisi segitiga lainnya dapat dihitung menggunakan perbandingan sisi-sisinya. Diketahui bahwa 30^o, 60^o, dan 90^o merupakan sudut istimewa, sehingga panjang sisi segitig siku-siku berupa perbandingan bilangan real positif.

Baca Juga: Cara Menghitung Tinggi Limas T.ABCD

Perbandingan Sisi Segitiga Siku-Siku dengan Sudut Istimewa 30^o, 60^o, dan 90^o

Sebuah segitiga siku-siku dengan sudut isitimewa 30^o, 60^o, dan 90^o memiliki perbandingan panjang sisi 1 : √3 : 2. Perbandingan panjang sisi segitiga siku-siku tersebut diperoleh dengan beberapa langkah yang memanfaatkan sifat-sifat segitiga.

Sifat yang digunakan adalah sifat pada segitiga sama sisi yaitu ketiga panjang sisinya sama panjang dan ketiga sudutnya sama besar. Sesuai sifatnya, besar ketiga sudut pada segitiga sama sisi adalah 60^o. Jika dari salah satu titik segitiga dibuat garis bagi maka akan terbentuk segitiga siku-siku. Besar dua buah sudut lainnya pada segitiga siku-siku yang terbentuk adalah 30^o dan 60^o.

Jika segitiga sama sisi pada awalnya memiliki panjang 2 satuan maka akan terbentuk segitiga siku-siku dengan panjang sisi miring 2 dan salah satu sisi tegaknya adalah 1 satuan. Panjang sisi tegak pada segitiga siku-siku yang lainnya dapat dihitung menggunakan teorema Pythagoras.

Sehingga, dapat diperoleh perbandingan sisi segitiga siku-siku dengan sudut istimewa 30^o, 60^o, dan 90^o adalah 1 : √3 : 2.

Perbandingan Sisi Segitiga Siku-Siku dengan Sudut Istimewa 45^o, 45^o, dan 90^o

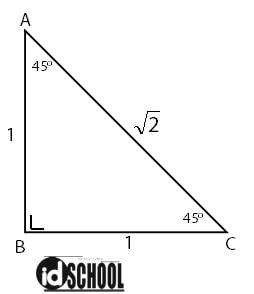
Segitiga siku-siku dengan sudut istimewa 45^o, 45^o, dan 90^o merupakan segitiga siku-siku sama kaki. Sisi-sisi yang menghadap sudut dengan besar 45^o pada segitiga siku-siku sama kaki merupakan sisi tegak. Sementara sisi segitiga yang menghadap sudut dengan besar 90^o merupakan sisi miring.

Panjang sisi segitiga yang berhadapan dengan besar sudut yang sama akan sama panjang. Sehingga, panjang sisi yang menghadap besar sudut 45^o adalah sama panjang.

Andaikan panjang sisi tegak segitiga siku-siku adalah 1 satuan maka sisi miring segitiga siku-siku dapat diketahui. Berdasarkan teorema pythagoras, panjang sisi miring untuk segitiga siku-siku dengan sudut istimewa 45^o, 45^o, dan 90^o adalah √2.

Sehingga dapat diperoleh perbandingan panjang sisi segitiga siku-siku dengan istimewa 45^o, 45^o, dan 90^o sama dengan 1 : 1 : √2.

Perbandingan Sisi Segitiga Siku-Siku dengan Sudut Istimewa 37^o, 53^o, dan 90^o

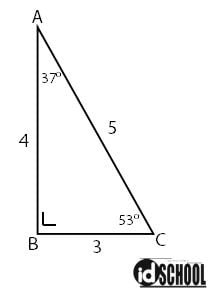
Berikutnya adalah segitiga siku-siku dengan sudut istimewa 37^o, 53^o, dan 90^o. Segitiga siku-siku dengan besar ketiga sudut 37^o, 53^o, dan 90^o memiliki perbandingan panjang sisi-sisi segitiga yaitu 3 : 4 : 5. Sisi terpanjang merupakan bagian sisi segitiga yang menghadap sudut 90^o atau sudut siku-siku. Sedangkan sudut terpendeknya adalah sisi segitiga yang menghadap sudut 37^o.

Baca Juga: Jenis – Jenis Segitiga

Contoh Penggunaan Rumus Perbandingan Sisi Segitiga Siku-Siku

Dari tiga bahasan di atas dapat diperoleh 3 perbandingan panjang sisi segitiga siku-siku dengan sudut istimewa. Di mana ketiga perbandingan antara besar sudut segitiga dengan panjajang sisi segitiga sesuai dengan nilai-nilai berikut.

Perbandingan besar sudut dan panjang sisi segitiga siku-siku:

• 30^o : 60^o : 90^o = 1 : √3 : 2
• 45^o : 45^o : 90^o = 1 : 1 : √2
• 37^o : 53^o : 90^o = 3 : 4 : 5

Perbandingan sisi segitiga siku-siku dengan sudut istimewa dapat digunakan untuk menyelesaikan masalah pada soal di bagian pengantar. Pada permasalahan sebelumnya diketahui segitiga PQR siku-siku di Q dengan besar sudut P = 30^o dan panjang sisi PR = 18 cm.

Panjang sisi PQ dan QR dapat dicari menggunakan perbandingan sisi segitiga siku-siku. dengan sudut istimewa 30^o, 60^o, dan 90^o.

Perhatikan bahwa segitiga ABC dan segitiga PQR sebangun, sehingga sisi PQ dan QR dapat dihitung dengan perbandingan sisi segitiga siku-siku 30^o : 60^o : 90^o = 1 : √3 : 2.

Menghitung panjang sisi PQ:

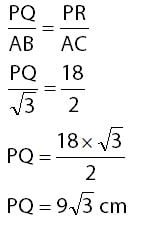
Menghitung QR:

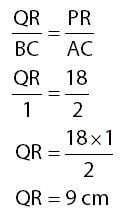
Jadi, panjang sisi PQ dan QR pada segitiga PQR secara urut sama dengan 9√3 cm dan 9 cm.

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Perbandingan Sisi Segitiga Siku-Siku

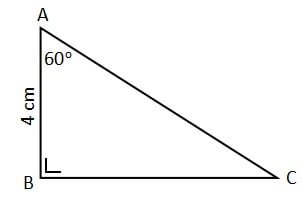
Panjang sisi AC adalah ….
A. 4√2 cm
B. 4√3 cm
C. 8 cm
D. 8√3 cm

Pemabahasan:
Pada soal terdapat sebuah segitiga siku-siku dengan beberapa informasi seperti berikut.

• Panjang sisi AB = 4 cm
• Besar sudut A: ∠A = 60^o
• Segitiga siku-siku di sudut B (besar sudut B: ∠B = 90^o)
• Besar sudut C: ∠C = 180^o ‒ (90^o + 60^o) = 30^o

Diketahui perbandingan besar sudut A : B : C = 60^o : 90^o : 30^o, sehingga perbandingan sisi segitiga siku-siku adalah AB : BC : AC = 1 : √3 : 2.

Menghitung panjang sisi AC:
^AC/_AB = ²/₁
^AC/₄ = ²/₁
1 × AC = 4 × 2
AC = 8 cm

Jadi, panjang sisi AC sama dengan cm

Jawaban: C

Contoh 2 – Soal Perbandingan Sisi Segitiga Siku-Siku

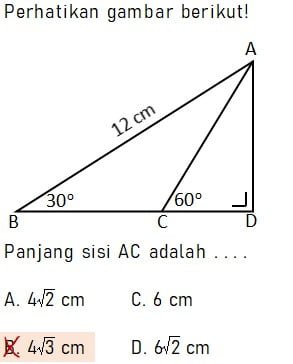
Pembahasan:
Dari soal dapat diketahui dua buah sergitiga siku-siku yaitu segitiga ABD dan ACD yang keduanya siku-siku di titik D (besar ∠ADB = ∠ADC = 90^o). Di mana besar sudut dan panjang sisi yang diketahui sesuai dengan nilai-nilai di bawah

• Besar sudut ABD: ∠ABD = 30^o 
• Besar sudut ACD: ∠ACD = 60^o
• Panjang sisi AB = 12 cm

Sehingga dapat diketahui bahwa besar ∠BAD = 60^o dan besar ∠CAD = 60^o. Maka perbandingan sisi segitiga untuk kedua segitiga tersebut adalah,

• ∠ABD : ∠BDA : ∠BAD = 30^o : 90^o : 60^o 
  AD : AB : BD = 1 : 2 : √3
• ∠ACD : ∠CDA : ∠CAD = 60^o : 90^o : 30^o
  AD : AC : CD = √3 : 2 : 1
• Dapat diperoleh dua perbandingan sisi segitiga siku-siku yaitu,
  AD : AB = 1 : 2
  AD : AC = √3 : 2.

Menentukan hubungan panjang sisi AD dan AC:
AD : AC = √3 : 2
^AD/_AC = ^√3/₂
AD = ^√3/₂AC

Menghitung nilai AC:
AD : AB = 1 : 2
AD : 12 = 1 : 2
^AD/₁₂ = ¹/₂
2 × AD = 1 × 12
2 × ^√3/₂AC = 1 × 12
√3AC = 12
AC = ¹²/_√3 = ¹²/₃√3 = 4√3 cm

Jadi, panjang sisi AC sama dengan 4√3 cm.

Jawaban: B

Demikianlah ulasan materi perbandingan sisi segitiga siku-siku dengan sudut istimewa. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Pembuktian Jumlah Ketiga Sudut Segitiga = 180^o