Cara Menghitung Luas Selimut Tabung (+Contoh Soal dan Pembahasan)

Cara menghitung luas selimut tabung dapat dilakukan menggunakan rumus luas selimut tabung L_{selimut tabung} = 2πr × t_tabung atau L_{selimut tabung} = πd × t_tabung. Di mana r adalah jari-jari tabung dan d adalah diameter tabung, sementara t_tabung adalah tinggi tabung dan π = ²²/₇ atau π = 3,14.

Sebuah bangun berbentuk tabung memiliki jaring-jaring yang terdiri dari dua buah lingkaran kembar dan sebuah persegi panjang. Dua buah lingkaran pada jaring-jaring tabung tersebut merupakan alas dan tutup tabung. Sehingga, luas bagian atap atau alas tabung dapat dihitung dengan luas lingkaran L = πr².

Sedangkan luas selimut tabung yang berbentuk persegi panjang dapat diperoleh dengan perkalian panjang dan lebarnya. Di mana, panjang selimut tabung sama dengan keliling lingkaran (K = 2πr atau K = πd) pada bagian atas/tutup tabung dan lebarnya sama dengan tinggi tabung. Sedangkan lebar selimut tabung sama dengan tinggi tabung (t). Jadi, rumus luas selimut tabung dapat dinyatakan melalui persamaanL = 2πrt atau L = πdt.

Bagaimana cara menghitung luas selimut tabung? Sobat idschool dapat mencari tahu bagaimana caranya melalui ulasan di bawah!

Table of Contents

• Bentuk Tabung
• Rumus Seluruh Luas Permukaan Tabung
• Rumus Luas Selimut Tabung
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Penerapan Rumus Tabung
  • Contoh 2 – Soal Luas Selimut Tabung
  • Contoh 3 – Soal Luas Selimut Tabung

Baca Juga: Kumpulan 8 Rumus Luas dan Keliling Bangun Datar

Bentuk Tabung

Tabung adalah bangun ruang yang terdiri dari 2 buah rusuk berupa lengkungan (rusuk lengkung), 3 buah sisi, dan tidak memiliki titik sudut. Ketiga sisi pada tabung meliputi sisi atap, alas, dan selimut tabung. Dua rusuk pada tabung membentuk dua lingkaran yang memisahkan alas dan atap tabung dengan selimut tabung.

Alas dan tutup tabung adalah dua lingkaran identik yang terletak sejajar dengan jarak sama dengan tinggi tabung. Bagian selimut tabung adalah bagian yang menyelimuti ruangan antara alas dan tutup tabung .

Bangun ruang berbentuk tabung beserta jaring-jaring tabung pada umumnya terdapat pada gambar berikut.

Baca Juga: Rumus Volume dan Luas Permukaan Tabung

Rumus Seluruh Luas Permukaan Tabung

Seluruh permukaan tabung terdiri dari dua buah luas lingkaran sebagai alas dan tutup tabung, serta luas selimut tabung. Sehingga luas seluruh permukaan tabung dapat dihitung melalui persamaman L_{permukaan tabung} = 2πr² + πrt.

Di mana r adalah jari-jari lingkaran pada bagian alas/tutup tabung dan s adalah tinggi tabung. Sedangkan π (dibaca: pi) adalah konstanta dalam matematika yang menyatakan perbandingan antara keliling lingkaran dengan diameternya dengan nilai π = ²²/₇ atau π = 3,14.

• Jika jari-jari bernilai kelipatan 7 maka nilai π yang digunakan adalah π = ²²/₇
• Jika jari-jari bernilai kelipatan 10 atau bilangan lain menggunakan nilai π = 3,14

Luas permukaan tabung merupakan jumlah dari luas sisi-sisi yang menyusun tabung. Jika dilihat melalui jaring-jaring tabung maka luas permukaan tabung sama dengan luas gabungan dari bangun datar penyusunnya. Jaring-jaring tabung terdiri dari dua buah lingkaran dan sebuah persegi panjang.

Sehingga luas seluruh permukaan tabung dapat dihitung melalui rumus L_permukaan = 2πr² + πrt atau disederhanakan menjadi L_permukaan = 2πr × (r + t).

Baca Juga: Cara Menghitung Volume Gabungan (+Contoh Soal dan Pembahasan)

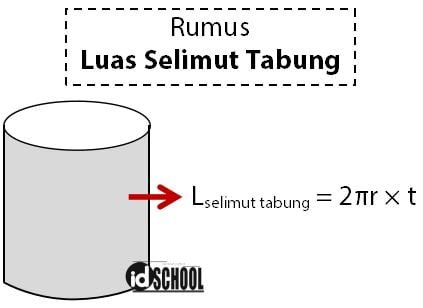
Rumus Luas Selimut Tabung

Luas selimut tabung menunjuk pada bagian tabung berupa sisi lengkung pada bagian samping. Pada jari-jari tabung, bentuk selimut tabung berupa persegi panjang yang nilai panjangnya sama dengan keliling lingkaran dan lebarnya sama dengan tinggi tabung.

Diketahui bahwa keliling lingkaran dapat dihitung melalui rumus K_ʘ = 2πr atau K_ʘ = πd. Sehingga besar luas selimut tabung dapat dihitung melalui perkalian antara K_ʘ = 2πr atau K_ʘ = πd dengan tinggi tabung (t).

Baca Juga: Rumus Luas Permukaan dan Volume Kerucut

Contoh Soal dan Pembahasan

Beberapa soal di bawah dapat digunakan untuk menambah pemahaman bahasan cara menghitung luas selimut tabung. Setiap contoh soal yang diberikan telah dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan soal tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Penerapan Rumus Tabung

Luas permukaan tabung dengan diameter alas 42 cm adalah 4.092 cm². Luas selimut tabung tersebut adalah ….
A. 1.350 cm²
B. 1.340 cm²
C. 1.330 cm²
D. 1.320 cm²

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Diameter alas tabung: d = 42 cm
• Jari-jari tabung: r = ¹/₂d = ¹/₂ × 42 = 21 cm
• Luas permukaan tabung: L_permukaan = 4.092 cm²

Menghitung luas selimut tabung:
L_{permukaan tabung} = 2πr² + L_{selimut tabung}
L_{permukaan tabung} = 2ײ²/₇×21² + L_{selimut tabung}
4.092 = 2.772 + L_{selimut tabung}
L_{selimut tabung} = 4.092 – 2.772 = 1.320 cm²

Jadi, luas selimut tabung tersebut adalah 1.320 cm².

Jawaban: D

Contoh 2 – Soal Luas Selimut Tabung

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut (misalkan jari-jari tabung = r dan diameter tagbung = d).

• Tinggi tabung = diameter bola: t_tabung = d = 2r
• Jari-jari tabung = jari-jari bola: r_tabung = r
• Luas permukaan bola: L_{permukaan bola} = 154 cm²

Menentukan jari-jari bola:
L_{permukaan bola} = 4πr²
154 = 4 × ²²/₇ ×r²
154 = ⁸⁸/₇ × r²
r² = 154 × ⁷/₈₈
r² = 12,25 → r = 3,5 cm

Dari perhitungan dapat diketahui bahwa jari-jari bola adalah 3,5 cm. Sehingga jari-jari tabung r = 3,5 dan tinggi tabung t = 2 × 3,5 = 7 cm.

Menghitung luas selimut tabung:
L_{selimut tabung} = 2πrt
L_{selimut tabung} = 2 × ²²/₇ × 3,5 × 7 = 154 cm²

Jadi, luas selimut tabung adalah 154 cm².

Jawaban: A

Contoh 3 – Soal Luas Selimut Tabung

Perhatikan gambar di bawah!

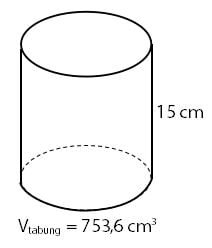
Luas selimut tabung pada gambar di atas adalah ….
A. 367,8 cm²
B. 368,7 cm²
C. 376,8 cm²
D. 378,6 cm²

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Isi/volume tabung: v_tabung = 753,6 cm³
• Tinggi tabung: t = 15 cm

Mencari tahu jari-jari tabung:
V_tabung = πr²t
V_tabung = 3,14 × r² × 15
753,6 = 47,1 × r²
r² = ^753,6/_47,1
r² = 16 cm
r = 4 cm

L_{selimut tabung} = 2πrt
L_{selimut tabung} = 2 × 3,14 × 4 × 15 = 376,8 cm²

Jadi, Luas selimut tabung pada gambar di atas adalah 367,8 cm².

Jawaban: C

Demikianlah tadi ulasan cara menghitung luas selimut tabung yang disertai dengan contoh soal dan pembahasannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Bangun Ruang Sisi Lengkung