Ada empat bentuk rumus jumlan n suku pertama yang memiliki notasi Sn. Meliputi dua rumus jumlah n suku pertama (Sn) untuk deret aritmatika. Dan dua rumus untuk jumlah n suku pertama atau Sn untuk deret geometri.
Deret aritmatika dan deret geometri merupakan penjumlahan bilangan-bilangan dari suatu barisan aritmatika atau geometri. Bentuk deret dapat dituliskan dalam penjumlahan barisan bilangan arau rumus notasi sigma.
Misalnya pada barisan bilangan aritmatika 1, 6, 11, 16, 21, 26, 31, 36, …. memiliki bentuk deret aritmatika 1 + 6 + 11 + 16 + 21 + 26 + 31 + … = Ʃni = 1 (i + 5). Aturan yang sama berlaku untuk deret geometri, misalnya pada deret 1 + 1/2 + 1/4 + …. = Ʃni=1 1/2i − 1.
Rumus Sn sama dengan penjumlahan n suku pertama dari deret aritmatika atau geometeri. Sebagai contoh, untuk menjumlahkan 5 suku pertama dicari S5. Bagaimana cara menghtiung jumlah n suku pertama? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Baca Juga: Pola Bilangan dan Rumus Un dari Pola Bilangan
Rumus Jumlah n Suku Pertama (Sn) Deret Aritmatika
Deret aritmatika adalah penjumlahan suku-suku pada barisan bilangan aritmatika. Contoh barisan aritmatika adalah 1, 2, 3, 4, 5, 6, …, Un (memiliki beda b = 1 untuk setiap kenaikan sukunya). Bentuk deret aritmatika untuk contoh barisan bilangan tersebut adalah 1 + 2 + 3 + 4 + 5 + 6 + … = Sn.
Ada dua rumus Sn deret aritmatika yang dapat digunakan yaitu Sn = n/2(a + Un) dan Sn = n/2[2a + (n-1)b]. Rumus Sn deret aritmatika bentuk pertama biasanya digunakan saat nilai Un diketahui. Sementara rumus Sn deret aritmatika bentuk kedua digunakan saat Un belum diketahui.

Baca Juga: Cara Menentuan Satuan Bilangan Berpangkat Banyak
Rumus Jumlah n Suku Pertama (Sn) Deret Geometri
Deret geometeri adalah penjumlahan bilangan-bilangan dari suatu barisan geometri. Contoh barisan geometri adalah 1, 1/2, 1/4, …, 1/2n−1. Bentuk deret dari barisan geometri tersebut adalah 1 + 1/2 + 1/4 + … + 1/2n−1.
Penjumlahan n bilangan deret geometri dinyatakan dalam rumus Sn. Ada dua bentuk rumus Sn deret geometri yaitu rumus Sn unutk rasio r > 1 dan rumus Sn untuk rasio r < 1.

Baca Juga: Aritmatika Sosial
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idshcool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selemat Berlatih!
Contoh 1 – Soal Jumlah n Suku Deret Aritmatika
Diketahui rumus jumlah suku ke-n barisan aritmatika adalah Un = 2n − 5. Jumlah delapan suku pertama barsian aritmatika tersebut adalah ….
A. 32
B. 44
C. 56
D. 64
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal, diketahui rumus suku ke-n barisan aritmatika Un = 2n − 5. Dari rumus Un tersebut dapat diperoleh nilai-nilai bilangan barisan aritmatika seperti pada tabel berikut.
| n | Un |
| 1 | U1 = 2(1) − 5 = 2 − 5 = −3 |
| 2 | U2 = 2(2) − 5 = 4 − 5 = −1 |
| 3 | U3 = 2(3) − 5 = 6 − 5 = 1 |
| … | dan seterusnya |
Diperoleh barisan aritmatika: −3, −1, 1, ….
- Suku pertama: U1 = a = −3
- Beda: b = −1−(−3) = 1−(−3) = … = 2
Akan dihitung jumlah delapan suku pertama (S8) deret tersebut. Substitusi nilai n = 8, a = −3, dan b = 2 pada rumus Sn deret aritmatika untuk menghitung S8.
Menghitung jumlah delapan suku pertama:
Jadi, jumlah delapan suku pertama barsian aritmatika tersebut adalah 32.
Jawaban: A
Contoh 2 – Jumlah n Suku Deret Aritmatika
Jumlah semua bilangan kelipatan 3 dan 4 antara 200 dan 450 adalah ….
A. 8.700
B. 6.804
C. 6.360
D. 6.300
Baca Juga: Barisan dan Deret
Pembahasan:
Bilangan kelipatan 3 dan 4 antara 200 dan 450 adalah bilangan-bilangan yang habis dibagi KPK dari 3 dan 4 yaitu 12.
Bilangan kelipatan 12 pertama yang berada antrara 200 dan 450 adalah 204. Sementara bilangan kelipatan 12 terakhir yang berada antara 200 dan 450 adalah 444.
Berdasarkan soal maka dapat dibentuk deret aritmatika dengan beda b = 12, suku pertama a = 204, dan suku terakhir Un = 444.
Deret matematika yang dibentuk oleh bilangan kelipatan 3 dan 4 antara 200 dan 450 tersebut adalah 204 + 216 + 228 + … + 444.
Pertama, perlu untuk mengetahui banyak suku bilangan (n) dari deret tersebut saat Un = 444.
Menentukan nilai n:
Un = a + (n ‒ 1)b
444 = 204 + (n ‒ 1)×12
444 ‒ 204 = 12n ‒ 12
240 + 12 = 12n
12n = 252
n = 252/12 = 21
Selanjutnya, jumlah 21 suku pertama untuk deret aritmatika 204 + 216 + 228 + … + 444 dapat dihitung seperti cara berikut.
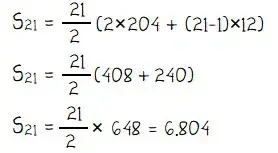
Jadi, jumlah semua bilangan kelipatan 3 dan 4 antara 200 dan 450 adalah 6.804
Jawaban: B
Contoh 3 – Jumlah n Suku Deret Geometri
Jumlah 5 suku pertama dari barisan geometri 4 + 2 + 1 + … adalah ….
A. 7,5
B. 7,75
C. 7,875
D. 7,9375
Pembahasan:
Dari deret 4 + 2 + 1 + … daat diketahui suku pertama deret geometri adalah U1 = a = 4 dan rasio r = 1/2. Substitusi nilai a = 4, r = 1/2, dan n = 5 ke rumus Sn deret geometri untuk mencari nilai jumlah 5 suku pertama dari barisan geometri tersebut,
Menghitung jumlah 5 suku pertama barisan geometri 4 + 2 + 1 + … :
= 4 × (32/32 − 1/32) × 2/1
= 8 × 31/32 = 7,75
Jadi, jumlah 5 suku pertama dari barisan geometri 4 + 2 + 1 + … adalah S8 = 7,75
Jawaban: B
Demikianlah tadi ulasan rumus jumlah n suku pertama (Sn) untuk deret aritmatika dan geometri. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Pola Bilangan 2 Tingkat
Pembahasan Contoh 2 tidak ada ya min?
Halo Quadrad, sudah ditambahkan ya… terima kasih atas kunjungan dan komentarnya!