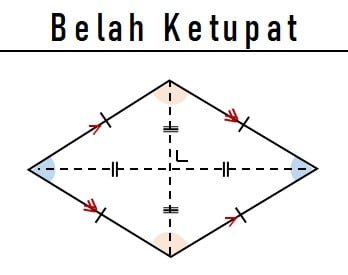
Keliling belah ketupat merupakan jumlah semua sisi yang membatasi bangun berbentuk belah ketupat. Sedangkan luas belah ketupat adalah area atau wilayah dari bangun berbentuk belah ketupat. Belah ketupat atau Rhombus adalah bangun datar berbentuk segi empat dengan empat sisinya sama panjang, tetapi belah ketupat bukan persegi. Dua pasang sisi pada belah ketupat saling sejajar dan setiap sisi yang tidak sejajar akan saling berpotongan membentuk suatu sudut. Besar setiap sudut yang berlawanan adalah sama, sedangkan jumlah dua sudut yang saling berdekaran sama dengan 180o.
Rhombus (belah ketupat) bersama dengan persegi dan persegi panjang termasuk dalam parallelogram (jajar genjang). Di mana bangun-bangun tersebut merupakan bangun datar yang mempunyai dua pasang sisi saling sejajar. Belah ketupat memiliki dua diagonal yang saling berpotongan tegak lurus (membentuk sudut 90o). Perpotongan antara dua diagonal membagi kedua diagonal sama panjang.
Baca Juga: Rumus Keliling dan Luas Trapesium (+Contoh Soal dan Pembahasan)
Bagaimana cara menghitung keliling belah ketupat? Bagaimana cara menghitung luas belah ketupat? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Rumus Keliling Belah Ketupat
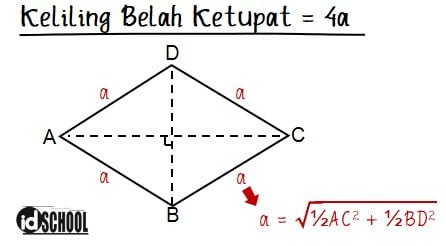
Keliling belah ketupat sama dengan jumlah empat buah sisi yang menyusunnya. Diketahui bahwa keempat sisi belah ketupat adalah sama panjang. Misalkan panjang sisi belah ketupat adalah a, maka rumus keliling belah ketupat adalah K = 4a.
Satuan keliling belah ketupat biasanya menggunakan senti meter (cm) atau meter (m).
Rumus Luas Belah Ketupat
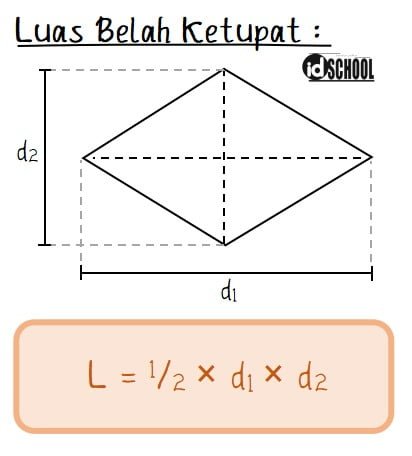
Luas belah ketupat adalah daerah yang dibatasi oleh dua pasang sisi yang saling sejajar dan berpotongan. Besar daerah tersebut dapat dihitung dari perkalian diagonal dibagi dua. Misalkan panjang dua diagonal belah ketupat adalah d1 dan d2, maka luas belah ketupat sama dengan L = 1/2 × d1 × d2.
Satuan belah ketupat biasanya menggunakan senti meter persegi (cm2) atau meter persegi (m2).
Baca Juga: Pasangan Garis Sejajar, Berpotongan, dan Bersilangan pada Limas TABCD
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Luas Belah Ketupat
Panjang sisi belah ketupat ABCD adalah 5 cm dan panjang diagonal AC adalah 8 cm. Luas belah ketupat ABCD adalah ….
A. 48 cm2
B. 36 cm2
C. 32 cm2
D. 24 cm2
Pembahasan:
Dari soal dapat diperoleh informasi bahwa panjang sisi belah ketupat ABCD adalah 5 cm dan panjang salah satu diagonalnya adalah AC = 8 cm. Agar dapat menghitung panjang satu diagonal belah ketupat lainnya yang belum diketahui yaitu BD.
Panjang diagonal BD dapat dihitung dengan Teorema Pythagoras seperti pada cara berikut.
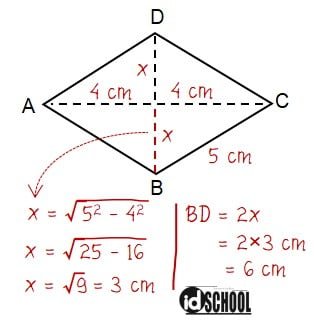
Diperoleh panjang diagonal BD = 6 cm, sehingga luas belah ketupat ABCD selanjutnya dapat dihitung.
Menghitung luas belah ketupat ABCD (L):
L = ½ × AC × BD
L = ½ × 8 × 6
L = 24 cm2
Jawaban: C
Contoh 2 – Soal Keliling Belah Ketupat
Diketahui panjang dua diagonal belah ketupat PQRS adalah 12 cm dan 16 cm. Keliling belah ketupat PQRS adalah ….
A. 64 cm
B. 48 cm
C. 40 cm
D. 32 cm
Pembahasan:
Keliling belah ketupat PQRS dapat dihitung dengan menjumlahkan keempat sisi belah ketupat. Panjang sisi dari belah ketupat PQRS belum diketahui sehingga perlu dihitung terlebih dahulu.
Diketahui bahwa panjang kedua diagonal belah ketupat PQRS adalah d1 = 12 cm dan d2 = 16 cm. Panjang sisi belah ketupat dapat dihitung dengan Teorema Pythagoras seperti pada cara yang ditunjukkan berikut.
Menghitung panjang sisi belah ketupat:
s2 = (½d1)2 + (½d2)2
s2 = (½×12)2 + (½×16)2
s2 = 62 + 82
s2 = 36 + 64 =100
s = √100 = 10 cm
Menghitung keliling belah ketupat PQRS:
KPQRS = 4×s
KPQRS = 4×10 = 40 cm
Jadi, keliling belah ketupat PQRS sama dengan 40 cm.
Jawaban: C
Contoh 3 – Soal Luas Belah Ketupat
Panjang diagonal-diagonal suatu belah ketupat diketahui berturut-turut 15 cm dan (2x ‒ 2) cm. Jika luas belah ketupat tersebut adalah 135 cm2 maka nilai x yang memenuhi adalah ….
A. 9
B. 10
C. 18
D. 20
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
- Panjang diagonal pertama: d1 = 15 cm
- Panjang diagonal ke dua: d2 = (2x ‒ 2) cm
- Luas belah ketupat: 135 cm2
Menentukan nilai x:
Luas belah ketupat = 135
½× d1 × d2 = 135
½× 15 × (2x ‒ 2) = 135
15 × (2x ‒ 2) = 135 × 2
30x ‒ 30 = 270
30x = 270 + 30
30x = 300
x = 300/30 = 10
Jadi, nilai x yang memenuhi adalah 10.
Jawaban: C
Contoh 4 – Soal Luas Belah Ketupat

Pembahasan:
Keterangan pada soal memberikan informasi bahwa keliling belah ketupat sama dengan 52 cm. Dari informasi tersebut dapat diperoleh keempat panjang sisi belah ketupat AB = BC = CD = DA = 52 : 4 = 13 cm.
Misalkan kedua diagonal belah ketupat AC dan BD berpotongan di titik O maka panjang AO = OC = 24 : 2 = 12 cm. Sedangkan panjang BO = OD dapat dihitung dengan teorema Pythagoras seperti yang ditunjukkan cara berikut.
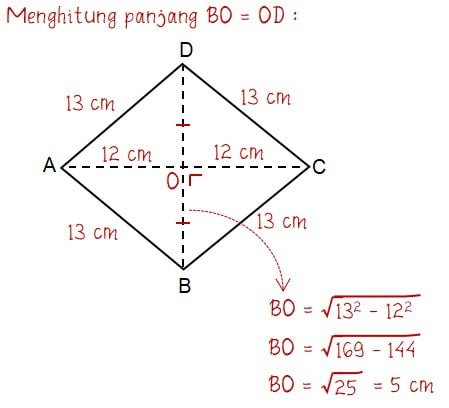
Darai hasil perhitungan diperoleh bahwa panjang BO = OD = 5 cm, sehingga panjang BD = BO + OD = 5 + 5 = 10 cm. Selanjutnya, luas belah ketupat dapat dihitung seperti cara berikut.
Menghitung luas belah ketupat ABCD:
LBelah Ketupat = ½ × AC × BD
LBelah Ketupat = ½ × 24 × 10
LBelah Ketupat = 120 cm2
Jadi, luas belah ketupat ABCD sama dengan 120 cm2.
Jawaban: C
Demikianlah tadi ulasan bagaimana cara menghitung keliling dan luas belah ketupat. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menghitung Luas Selimut Tabung