Trapesium merupakan bangun datar. Memiliki sepasang sisi sejajar. Jarak antara dua sisi sejajar trapesium merupakan tinggi trapesium. Rumus kesebangunan trapesium berguna untuk mengetahui panjang sisi-sisi trapesium.
Ada dua soal kesebangunan trapesium yang sering keluar dalam soal ujian. Pertama menanyakan panjangn garis EF. Dengan itik E dan titik F adalah titik pada kaki trapeisum. Bentuk kedua menananyakan panjang garis PQ. Dengan P dan Q adalah titik tengah dari masing-masing diagonal trapesium.
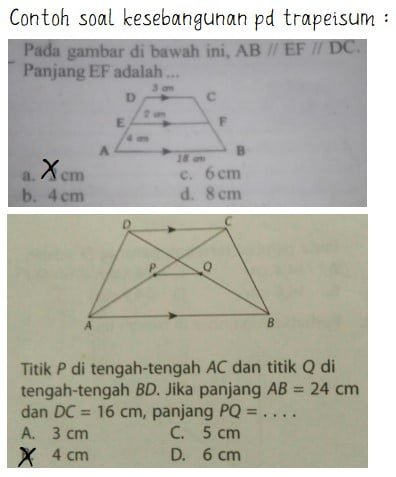
Penjelasan lebih lanjut mengenai rumus kesebangunan trapesium diberikan di bawah.
Daftar isi:
Baca Juga: Kesebangunan dan Kekongruenan
Kesebangunan Trapesium Bentuk 1
Diberikan sebuah trapesium ABCDE. Titik E berada pada kaki trapesium AD dan titik F berada pada kaki trapesium BC. Ruas garis EF sejajar dengan AB dan DC.
Panjang segmen garis EF dapat dicari menggunakan rumus kesebangunan trapesium berikut.
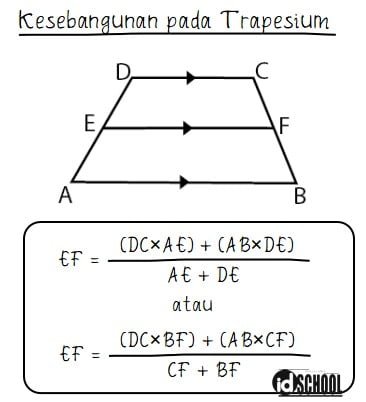
Rumus panjang garis EF di atas dicari melalui persamaan kesebangunan. Pembuktian dari persamaan di atas ditunjukkan melalui langkah pembuktian di bawah.
Pembuktian rumus kesebangunan trapesiuam bentuk 1:
Diberikan sebuah trapesium ABCD dan garis EF // AB dan EF // DC.
Pertama, buat garis DH sehingga menghasilkan sebuah segitiga dan jajar genjang. Gambarnya nampak seperti berikut.
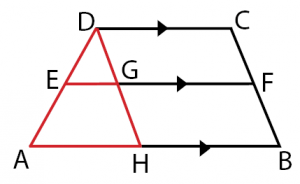
Keterangan:
DC = GF = HB
∆EDG ~ ∆ADH
Perhatikan ∆EDG dan ∆ ADH!
Berdasarkan kesebangunan, dapat dibentuk persamaan berikut.
Selanjutnya perhatikan bahwa EF = EG + GF. Sehingga,
EF = EG + GF
Nilai AH = AB ‒ HB , maka persamaan garis EF dapat dibentuk seperti berikut.
Karena GF = HB = DC dan DA = AE + DE maka dapat diperoleh persamaan berikut.
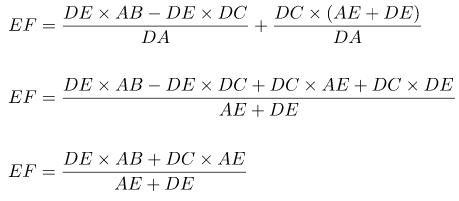
Diperoleh rumus kesebangunan trapesium untuk mencari panjang garis EF. Dengan cara yang sama, dapat juga diperoleh persamaan EF seperti di bawah.
Untuk melihat cara menggunakan rumus kesebangunan trapesium. Perhatikan penyelesaian contoh soal di bawah.
Contoh Soal 1
Perhatikan trapesium di bawah!

Panjang TU adalah ….
A. 14 cm
B. 15 cm
C. 16 cm
D. 19 cm
Pembahasan:
Diketahui panjang PQ = 10 cm, ST = 3 cm, SR = 25 cm, dan TP = 2cm.
Mencari Panjang TU:
Jadi, panjang TU adalah 16 cm.
Jawaban: C
Baca Juga: Jenis – Jenis Segitiga
Kesebangunan Trapesium Bentuk 2
Rumus kesebangunan trapesium bentuk 2 menghitung garis EF. Dengan titik E adalah titik tengah diagonal AC dan titik F adalah titik tengah diagonal BD. Sehingga AE : AC = BF : BD = 1: 2.
Rumus cepat untuk kesebangunan trapesium bentuk 2 diberikan seperti persamaan berikut.

Bagaimana rumus di atas diperoleh? Penjelasannya ada pada pembuktian di bawah.
Pembuktian:
Pertama, buat titik G yang merupakan perpanjangan garis EF. Gambarnya napak seperti berikut.

Perhatikan ∆BCD dan ∆BGF!
Bangun datar ∆BCD dan ∆BGF adalah dua buah segitiga yang sebangun, sehingga dapat diperoleh persamaan berikut.
Kita simpan persamaan di atas sebagai persamaan (1).
Selanjutnya, perhatikan ∆ABC dan ∆EGC seperti yang terlihat pada gambar di bawah.

Akan diperoleh persamaan berikut.
Kita simpan persamaan di atas sebagai persamaan (2).
Garis EG = EF + FG maka EF = EG – GF. Sehingga dari persamaan (1) dan persamaan (2) diperoleh persamaan berikut.
EF = EG – GF
Nilai BD = AC, sehingga bisa diperoleh persamaan berikut.
Diketahui bahwa AE : AC = 1 : 2 (E dan F merupakan titik tengah garis AC dan BD), maka AC = 2AE dan BF = FD = EC = AE.
Terbukti rumus cepat pada kesebangunan trapesium untuk mencari nilai EF = 1/2×(AB ‒ CD).
Contoh Soal 2:
Perhatikan gambar di bawah!

Jika E dan F adalah titik tengah diagonal AC dan BD maka panjang EF pada gambar di atas adalah ….
A. 4 cm
B. 8 cm
C. 16 cm
D. 32 cm
Pembahasan:
Dari soal diketahui panjang AB = 20 cm dan CD = 12 cm. Titik E dan F adalah titik tengah diagonal AC dan BD
Menghitung panjang segmen garis EF:
EF = 1/2(AB ‒ CD)
= 1/2×(20 ‒12)
= 1/2×8 = 4 cm
panjang EF pada gambar di atas adalah 4 cm (A).
Jawaban: A
Demikian pembahasan rumus kesebangunan pada trapesium beserta contoh soalnya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Kesebangunan pada Segitiga Siku – Siku
Great piece of content.