Luas Tembereng Lingkaran +Cara Menghitungnya

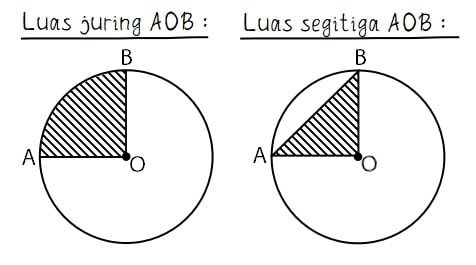
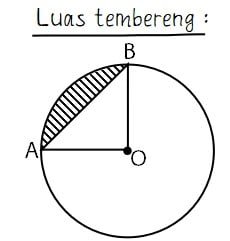
Tembereng adalah daerah yang dibatasi oleh sebuah busur lingkaran dan tali busur. Rumus umum luas tembereng adalah luas juring dikurangi luas segitiga. Misalkan sebuah tembereng dibatasi oleh busur AB dan tali busur AB. Maka Luas tembereng = luas juring AOB – luas segitiga AOB.

Juring lingkaran merupakan bagian dari luas lingkaran. Daerah juring lingkaran dibatasi oleh dua jari-jari dan sebuah busur lingkaran. Di dalam juring ligkaran terdapat segitiga yang dibatasi oleh dua buah jari-jari dan sebuah tali busur lingkaran. Selisih juring lingkaran dengan segitiga di dalamnya merupakan tembereng lingkaran.

Lebih lanjut mengenai luas tembereng lingkaran dan cara menghitungnya ada pada penjelesan di bawah.

Daftar isi:

• Rumus Luas Tembereng
• Cara menghitung luas tembereng lingkaran
• Contoh Soal dan Pembahasan
  • Contoh 1 – Tembereng yang terbenuk dari 1/4 lingkaran
  • Contoh 2 – Luas daerah yang diarsir adalah …
  • Contoh 3 – Luas tembereng yang mebentuk sudut 135^o
  • Contoh 4 – Tembereng yang diarsir pada gambar

Baca Juga: Segi Empat Tali Busur

Rumus Luas Tembereng

Diketahui sebuah lingkaran memiliki titik pusat pada titik O. Titik A dan B terletak pada busur lingkaran sehingga terdapat busur AB dan tali busur AB. Panjang jari-jari lingkaran tersebut adalah adalah OA = OB = r.

Sudut AOB adalah sudut pusat lingkaran. Sementara sudut OAB dan OBA adalah sudut keliling lingkaran. Gambar tembereng lingkaran merupakan daerah yang di arsir berikut.

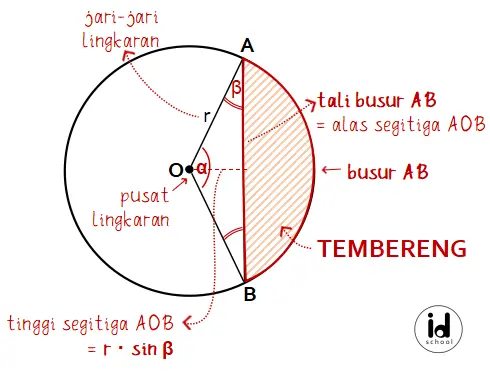
Untuk besar ∠AOB = ɑ serta besar ∠OAB dan ∠OBA = β maka:

Luas segitiga AOB = ¹/₂ × AB × (r × sin (^β/₂)^o)

Rumus luas tembereng lingkaran = luas juring AOB – luas segitiga AOB

Cara menghitung luas tembereng lingkaran

Ada tiga langkah yang perlu dilakukan untuk menghitung luasnya. Pertama adalah menghitung juring lingkaran, luas segitiga, dan terakhir menghitung temberengnya.

Bagaimana cara menghitung luasnya ditunjukkan melalui contoh soal tembereng lingkaran berikut.

Soal:
Tentukan luas tembereng lingkaran yang membentuk sudut AOB = 90° dan jari-jari lingkaran 28 cm!

Jawab:
Gambar tembereng lingkaran yang akan dicari luasnya terlihat seperti berikut.

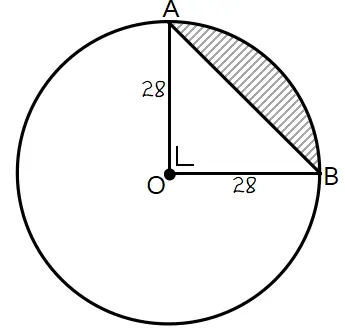
Luas juring lingkaran AOB sama dengan luas ¹/₄ lingkaran. Dan segitiga AOB merupakan segitiga sama kaki. Panjang alas segitiga AOB = tinggi segitiga AOB = panjang jari-jari lingkaran.

1) Menghitung luas juring AOB:

Luas juring AOB = ⁹⁰/₃₆₀ × (π × 14²)

= ¹/₄ × ²²/₇ × 28² = ¹/₄ × ²²/₇ × 28⁴ × 28

= ¹/₄ × 22 × 4 × 28 = 616 cm²

2) Menghitung luas segitiga AOB:

Luas segitiga AOB = ¹/₂ × a × t

= ¹/₂ × 14 × 14 = 98 cm²

3) Menghitung tembereng lingkaran

Luas = luas juring – luas segitiga

Luas = 154 − 98 = 56 cm²

Jadi, luas tembereng lingkaran yang membentuk sudut AOB = 90° dan jari-jari lingkaran 28 cm!

Contoh Soal dan Pembahasan

Beberapa contoh soal luas tembereng lingkaran dan penyelesaiannya ada di bawah.

Contoh 1 – Tembereng yang terbenuk dari 1/4 lingkaran

Sebuah tembereng yang terbentuk dari seperempat lingkaran yang berjari-jari 7 cm mempunyai luas ….
A. 7 cm²
B. 14 cm²
C. 21 cm²
D. 28 cm²

Pembahasan:
Tembereng terbentuk dari seperempat lingkaran. Artinya luas juring sama dengan luas seperempat lingkaran.

Luas juring = ¹/₄ × π × 7²

= ¹/₄ × ²²/₇ × 7 × 7

= ¹/₄ × 22 × 7 = 38,5 cm²

Segitiga di dalam juring memiliki panjang alas = tinggi segitiga = jari-jari lingkaran. Sehingga luas segitga = ¹/₂ × 7 × 7 = 24,5 cm².

Maka, sebuah tembereng yang terbentuk dari seperempat lingkaran yang berjari-jari 7 cm mempunyai luas = 38,5 cm² – 24,5 cm² = 14 cm².

Jawaban: B

Contoh 2 – Luas daerah yang diarsir adalah …

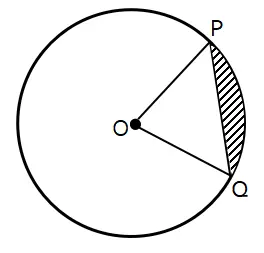
Pada gambar di atas, titik O adalah titik pusat lingkaran, besar ∠POQ = 60^o dan panjang OP = 30 cm. Luas daerah yang diarsir adalah ….
A. 471 cm²
B. 385,5 cm²
C. 358,5 cm²
D. 112,5 cm²

Pembahasan:
Besar ∠POQ = 60^o maka dapat diketahui bahwa segitiga POQ merupakan segitiga sama sisi. Sehingga OP = PQ = OQ = 7 cm (jari-jari lingkaran).

Luas segitiga POQ = ¹/₂ × PQ × (¹/₂ × PQ × sin 60^o)

= ¹/₂ × 30 × (¹/₂ × 30 × ¹/₂)

= ¹/₈ × 900 = 112,5 cm²

Jadi, luas tembereng = 471 − 112,5 = 358,5 cm².

Jawaban: C

Contoh 3 – Luas tembereng yang mebentuk sudut 135^o

Berapa luas tembereng yang membentuk sudut 135^o dengan jari-jari lingkaran 10 cm dan tali busur 12 cm adalah ….
A. 69,75 cm²
B. 68,25 cm²
C. 117,75 cm²
D. 118,25 cm²

Pembahasan:
Dari soal diketahui sebuah juring memiliki sudut pusat a = 135^o, jari-jari lingkaran r = 10 cm, dan panjang tali busur = 12 cm.

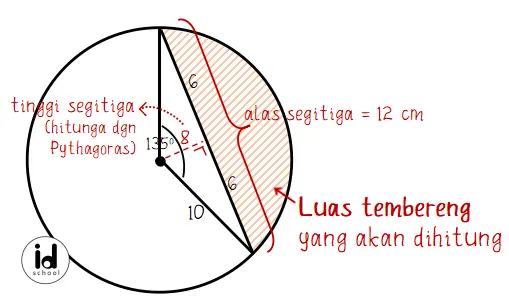
Sehingga,

Luas tembereng

Sehingga, luas tembereng yang membentuk sudut 135^o dengan jari-jari lingkaran 10 cm dan tali busur 12 cm adalah 69,75 cm².

Jawaban: A

Contoh 4 – Tembereng yang diarsir pada gambar

Jika panjang tali busur AB = 20 cm maka luas daerah yang diarsir pada gambar berikut

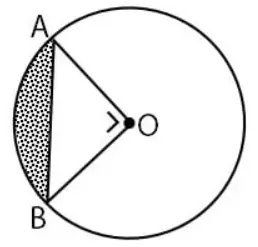
adalah ….
A. 57 cm²
B. 56 cm²
C. 47 cm²
D. 46 cm²

Pembahasan:
Segitiga AOB adalah segitiga siku-siku sama kaki dengan panjang sisi miring = AB = 20 cm.

Menghitung panjang jari-jaring lingkaran:

r² + r² = 20²

2r² = 400

r² = ⁴⁰⁰/₂ = 200

r = √200 = 10√2 cm

Diperoleh hasil panjang jari-jari lingkaran = 10√2 cm. Panjang jari-jari lingkaran selanjutnya digunakan untuk menghitung luas juring AOB dan luas segitiga AOB.

Menghitung luas juring AOB:

L_{juring AOB} = ⁹⁰/₃₆₀ × (π×r²)

L_{juring AOB} = ¹/₄ × (3,14 × (10√2)²) = 157 cm²

Menghitung luas segitiga AOB:

L_ΔAOB = ¹/₂×10√2×10√2

L_ΔAOB = ¹/₂×200 = 100 cm²

Jadi, Luas tembereng = Luas juring AOB − Luas segitiga AOB = 157 − 100 = 57 cm².

Jawaban: A

Demikianlah tadi ulasan cara menghitung luas tembereng. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!