Sudut antara dua tali busur adalah besar sudut yang dibentuk oleh perpotongan dua tali busur. Letak sudut perpotongan dapat berada di dalam lingkaran atau di luar lingkaran. Besar sudut antara dua tali busur yang berpotongan di dalam/luar lingkaran dapat dihitung menggunakan beberapa sifat besar sudut seperti sudut pusat = 2×sudut keliling, besar sudut lurus = 180o, dan lain sebagainya.
Dalam sebuah lingkaran terdapat pusat, jari-jari, diameter, busur, tali busur, apotema, tembereng, dan juring. Tali busur adalah sebuah ruas garis yang dibentuk dari menghubungkan 2 titik yang terletak pada lingkaran.
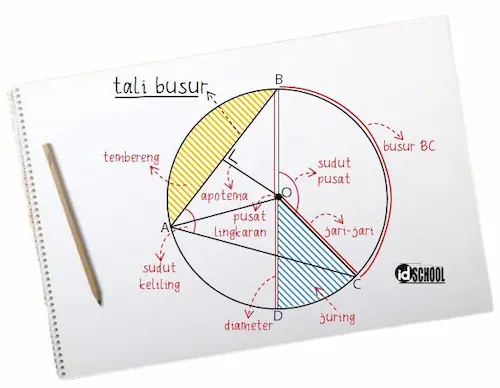
Bagaimana cara mengetahui besar sudut yang dibentuk oleh perpotongan dua tali busur? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Baca Juga: Luas Juring dan Panjang Busur Lingkaran
Besar Sudut Antara Dua Tali Busur yang Berpotongan di Dalam Lingkaran
Pada sebuah lingkaran dengan titik pusat O terdapat dua tali busur yaitu ruas garis AC dan BD. Dua tali busur tersebut berpotongan pada satu titik di dalam lingkaran, yaitu titik P.
Ada empat sudut yang dibentuk dari perpotongan dua tali busur tersebut. Keempat sudut tersebut adalah sudut APD, ∠APB, ∠BPC, dan ∠CPD.
Rumus besar sudut antara dua tali busur yang berpotongan di dalam lingkaran:
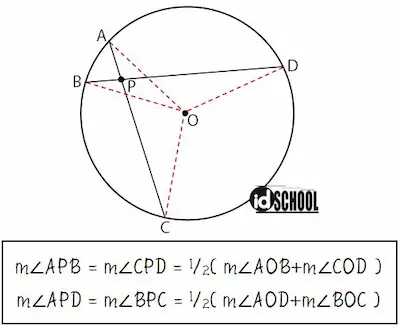
Dari mana rumus di atas di peroleh terdapat pada halaman pembuktian rumus sudut antara dua tali b
Empat sudut yang terbentuk merupakan dua pasang sudut yang saling bertolak belakang. Diketahui bahwa sifat besar sepasang sudut yang saling bertolak belakang adalah sama besar.
Sehingga terdapat dua pasangan besar sudut yang sama yaitu m∠APB = m∠CPD dan m∠BPC = m∠APD.
m∠APB = 1/2(m∠AOB + m∠COD)
m∠CPD = 1/2(m∠AOB + m∠COD)
Keterangan:
- m∠AOB = besar sudut pusat yang menghadap busur AB
- m∠COD = besar sudut pusat yang menghadap busur CD
m∠BPC = 1/2(m∠AOD + m∠BOC)
m∠APD = 1/2(m∠AOD + m∠BOC)
Keterangan:
- m∠AOD = besar sudut pusat yang menghadap busur AD
- m∠BOC = besar sudut pusat yang menghadap busur BC
Baca Juga: Lingkaran Dalam dan Luar Segitiga
Besar Sudut Antara Dua Tali Busur yang Berpotongan di Luar Lingkaran
Diketahui sebuah lingkaran dengan titik pusat O memiliki dua tali busur yaitu ruas garis AD dan BC. Kedua tali busur tersebut berpotongan pada titik P yang terletak di luar lingkaran. Terdapat sebuah sudut yang dibentuk oleh dua titik busur tersebut yaitu ∠CPD.
Besar ∠CPD mempunyai hubungan besar dua sudut pusat yaitu ∠COD dan ∠AOB. Rumus besar sudut antara dua tali busur yang berpotongan di luar lingkaran adalah sebagai berikut.
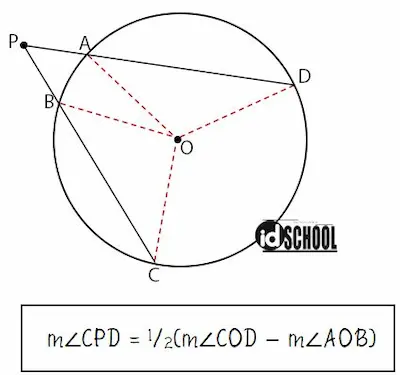
Dari mana rumus di atas di peroleh terdapat pada halaman pembuktian rumus sudut antara dua tali busur yang berpotongan di luar lingkaran.
Rumus besar sudut antara dua tali busur yang berpotongan di luar lingkaran = besar ∠CPD:
m∠CPD = 1/2(m∠COD − m∠AOB)
Keterangan:
- m∠COD = besar sudut pusat yang menghadap busur CD
- m∠AOC = besar sudut pusat yang menghadap busur AC
Baca Juga: Sudut Pusat dan Sudut Keliling Lingkaran
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Besar Sudut Antara 2 Tali Busur di Dalam Lingkaran
Pada gambar di bawah diketahui ∠MNL = 40o, ∠KLN = xo, dan ∠KTN = 3xo.
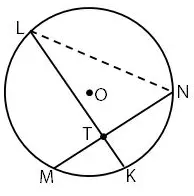
Besar ∠KTN = ….
A. 90o
B. 75o
C. 60o
D. 45o
Pembahasan:
Titik T adalah titik hasil perpotongan dua tali busur di dalam lingkaran. Perhatikan segitiga TLN dengan tiga sudutnya berjumalah 180o. Sehingga memenuhi persamaan m∠TLN + m∠LNT + m∠NTL = 180o.
Dari soal diketahui:
m∠TLN = m∠KLN = xo
m∠LNT = m∠MNL = 40o
m∠NTL = 180o ‒ m∠KTN = 180o ‒ 3xo
Menentukan nilai x:
xo + 40o + (180o ‒ 3xo) = 180o
xo ‒ 3xo = 180o ‒ 180o ‒ 40o
‒2xo = ‒40o
xo = ‒40/‒2 = 20o
Menghitung besar ∠KTN:
m∠KTN = 3xo
m∠KTN = 3×20o = 60o
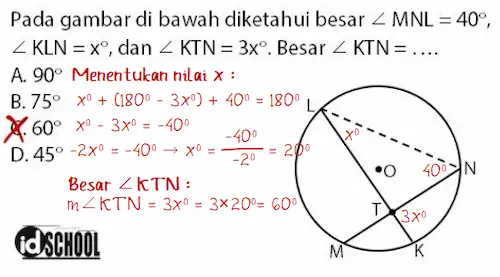
Jadi, besar ∠KTN = 3xo = 60o.
Jawaban: C
Baca Juga: Garis Singgung Persekutuan Dalam dan Luar Lingkaran
Contoh 2 – Soal Sudut Antara 2 Tali Busur di Luar Lingkaran
Perhatikan gambar berikut ini!

Jika diketahui besar ∠AOB = 80o dan besar ∠CAD = 14o maka besar ∠ADC = ….
A. 28o
B. 26o
C. 24o
D. 18o
Pembahasan:
∠ADC adalah sudut yang dibentuk oleh perpotongan dua ruas garis di luar lingkaran. Besar ∠ADC dapat diperoleh melalui perhitungan seperti cara di bawah.
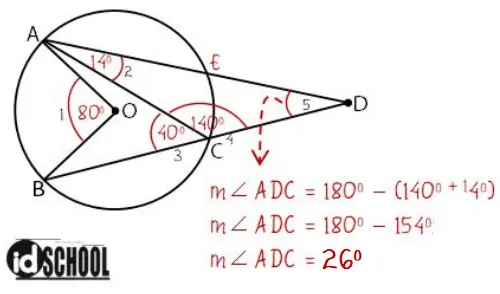
Jadi, besar ∠ADC = 26o.
Jawaban: B
Demikianlah tadi ulasan rumus besar sudut antara dua tali busur lingkaran yang bepotongan di dalam/luar lingkaran. Beserta dengan cara menggunakan kedua rumus tersebut. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Jawaban pada contoh soal 2 salah hitung
Holo Aurel, sudah dikoreksi ya :) Terima kasih atas kunjungan dan komentarnya