Contoh Soal PM UTBK SNBT 2024 dan Penjelasan Pembahasannya

Dari halaman simulasi-tes.bppp.kemdikbud.go.id memberikan sepuluh contoh soal PM UTBK SNBT 2024. Soal penalaran matematika (PM) yang diberikan teridiri dari dua permasalahan dengan setiap permasalahan memiliki lima pertanyaan. Permasalahan pertama dari contoh soal PM UTBK SNBT 2024 mengenai bianglala. Untuk permasalahan kedua dari contoh soal PM UTBK 2024 mengenai diagram lingkaran.

Setiap contoh soal PM UTBK SNBT 2024 yang diberikan sudah disertai pembahasannya. Sayangnya pembahasan contoh soal PM UTBK SNBT 2024 yang diberikan terlalu singkat dan perlu penjelasan lebih jelas lagi. Melalui halaman ini, idschool akan mengelaborasi agar lebih jelas lagi untuk pembaca setia idschool.

Pembahasan sepuluh contoh soal PM UTBK 2024 secara lebih jelas terdapat pada masing-masing penjelasan di bawah.

Bacaan 1 – Contoh Soal PM UTBK SNBT 2024

Sebuah bianglala (ferris wheel) bertitik pusat P(0, 0). Titik P berada pada ketinggian 35 meter dari permukaan tanah. Setiap bianglala naik dari titik terbawah, yaitu titik D. Dalam waktu 5 menit, setiap penumpuang bianglala terlah menjalani lintasan ^125π/₄ meter. Sebuah lampu dipasang pada suatu titik di bianglala.

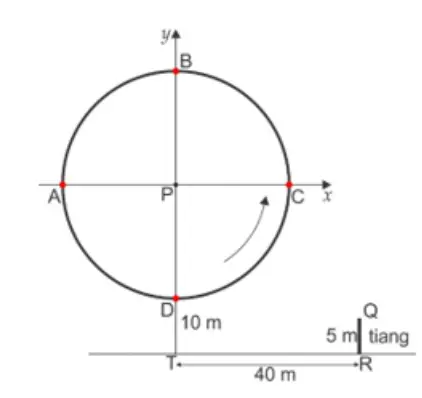
Soal 1

Bianglala berputar satu putaran dalam waktu … menit.
(A)  6
(B)  7
(C)  8
(D)  9
(E)  10

Jawab: (C)

Dari soal diketahui bahwa titik P berada pada ketinggian 35 meter dari permukaan tanah. Sehingga PT = 35 meter, sementara jarak DT = 10 m. Dengan demikian radius (jari-jari) bianglala tersebut adalah 35 – 10 = 25 meter.

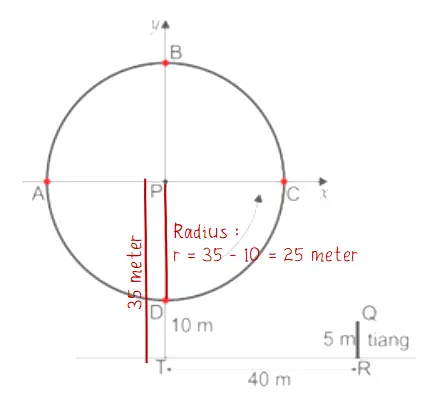
Panjang lintasan bianglala berputar satu putaran sama dengan keliling lingkaran (KO). Diketahui bahwa waktu untuk menempuh panjang lintasan ^125π/₄ meter adalah 5 menit.

Ringkasnya,

Antara waktu dan panjang lintasan memiliki hubungan senilai. Sehingga waktu yang dibutuhkan biang lala untuk berputar satu putaran dapat dihitung menggunakan perbandingan senilai seperti berikut.

Menentukan nilai x:

*kali silang

x = 2×4 = 8

Jadi, dalam 1 putaran diperlukan x = 8 menit.

Soal 2

Pada suatu saat seseorang berada pada titik B. Dua puluh menit kemudian, dia berada pada titik yang jaraknya ke garis AC adalah … meter.
(A)   0
(B)   10
(C)   12,5
(D)   20
(E)   25

Jawab: (E)

Dalam waktu 20 menit, bianglala berputar ²⁰/₈ = 2¹/₂ putaran. Setelah 20 menit, orang akan berada pada titik D. Jarak titik D ke garis AC sama dengan panjang jari-jari atau radius bianglala. Jadi, dia berada pada titik yang jaraknya ke garis AC adalah 25 meter.

Soal 3

Misalkan QR adalah tiang dengan tinggi 5 meter. Jarak terjauh antara lampu dan titik Q adalah ___  meter.

Jawab: 75

Misalkan lampu L adalah lampu pada bianglala yang terletak dengan jarak terjauh dari titik Q. Untuk koordinat titik P(0, 0) maka koordinat T(0, –35) dan koordinat Q(40, –30).

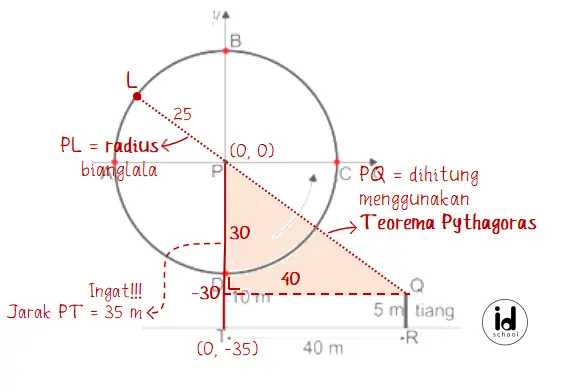
Menghitunng jarak titik Q ke pusat bianglala:

|PQ| = √(40² + (-30)²)

|PQ| = √(1.600 + 900)

|PQ| = √2.500 = 50 meter

Jarak terjauh antara lampu dan titik Q sama dengan panjang QL = PQ + PL = 50 + 25 = 75 meter. Jadi, jarak terjauh antara lampu dan titik Q adalah 75 meter.

Soal 4

Pada saat jarak lampu ke titik Q mencapai nilai terpendek, panjang bayangan tiang QR adalah … meter.
(A)   5²⁄₃ 
(B)   5
(C)   6¹⁄₃ 
(D)   6²⁄₃ 
(E)   7

Jawab: (D)

Saat lampu L berjarak terpendek dari tiang Q menghasilkan titik P’ yang merupakan titik ujung bayangan tiang QR. Misalkan titik S adalah perpotongan garis QR dengan sumbu X akan menghasilkan dua segitiga sebangun yaitu  ΔQSP dan ΔQRP.

Panjang bayangan tiang = RP’ dapat dihitung dengan perbandingan senilai dari sisi-sisi segitiga ΔQSP dan ΔQRP.

Jadi, panjang bayangan tiang QR adalah (D) 6²⁄₃ meter.

Soal 5

Misalkan titik U pada tanah adalah bayangan titik Q oleh lampu ketika bayangan tiang QR paling pendek. Titik V pada tanah adalah bayangan titik Q ketika bayangan tiang QR paling panjang. Titik A’ adalah bayangan titik Q di tanah ketika lampu berada di titik A. Ketika lampu berputar mulai dari titik A, urutan posisi bayangan titik Q di tanah adalah ….
(A)  A’-U-A’-B’-V-B’-A’
(B)  A’-B’-U-B’-A’-V-A’
(C)  A’-V-A’-B’-U-B’-A’
(D)  A’-B’-V-B’-A’-U-A’
(E)  A’-B’-U-B’-A’-V-A’

Jawab: (C)

• Diketahui:
  • Titik U = bayangan titik Q ketika bayangan tiang QR paling pendek
  • Titik V = bayangan titik Q ketika bayangan tiang QR paling panjang

Saat lampu di titik D, bayangan titik Q pada tanah berada di titik V (saat bayangan QR paling panjang). Kesimpulan ini diperoleh dengan cara menarik garis lurus dari titik D mengenai ujung atas tiang Q. Perpotongan garis lurus dengan tanah adalah titik V. Sehingga, titik V adalah bayangan titik Q di tanah ketika lampu berada di titik D.

Sementara saat lampu di titik C, bayangan titik Q pada tanah berada di titik U (saat bayangan QR paling pendek). Sebuag garis lurus yang mengenai ujung atas tiang QR akan berpotongan dengan tanah di titik U. Sehingga, titik U adalah bayangan titik Q di tanah ketika lampu berada di titik C.

Bianglala berputar berlawanan arah jarum jam (perhatikan anak panah putaran bianglala). Sehingga urutan putaran lampu adalah A – D – C – B – A.

Awalnya, bayangan titik Q dari lampu di titik A adalah A’ (1). Saat titik A mulai bergerak ke titik D, bayangan titik Q akan bergeser ke kanan yaitu titik V (2). Selanjutnya, lampu akan mengenai titik yang sejajar dengan titik A sehingga bayangan titik Q di tanah kembali berada di titik A’ (3).

Kemudian, lampu akan mengenai titik yang sejajar dengan titik B sehingga bayangan titik Q pada tanah berada di titik B’ (4). Berikutnya saat di titik C, bayangan titik Q pada tanah berada di titik U (5).

Bayangan titik Q pada tanah saat lampu berada di titik B adalah B’ (6). Dan bayangan titik Q pada tanah saat lampu berada di titik A adalah A’ (7). Jadi, bayangan titik Q menjejaki A’ – V – A’ – B’ – U – B’ – A’.

Bacaan 2 – Contoh Soal PM UTBK 2024

Diagram berikut menampilkan data mengenai populasi angkatan kerja di dua kecamatan, yaitu A dan B, pada tahun 2022 berdasarkan status bekerja, mengganggur, dan tidak aktif secara ekonomi.

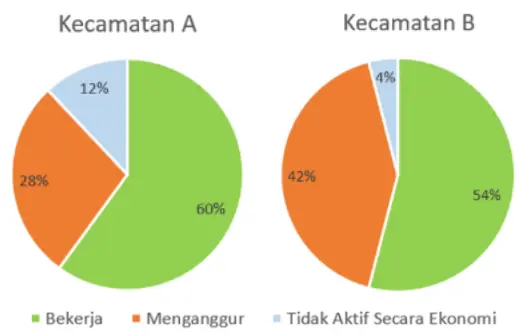
Diketahui populasi angkatan kerja di Kecamatan A adalah 15.000 orang, sedangkan di Kecamatan B adalah 10.000 orang.

Soal no 6

Klik pada kolom yang sesuai untuk tiap pernyataan berikut.

Jawab: Benar, Salah, Salah

Banyak populasi masing-masing untuk yang bekerja, menganggur, dan tidak aktif secara ekonomi di kecamatan A dan B di hitung dengan rumus persentase berikut.

Jika dinyatakan dalam bentuk tabel, data pada diagram dapat dinyatakan sebagai berikut.

Dari data dapat disimpulkan:

• Banyaknya orang yang bekerja di Kecamatan A adalah 9.000 orang < 10.000 orang. Jadi, pernyataan 1 Benar.
• Banyaknya orang yang menganggur di Kecamatan B adalah 4.200 orang = 4.200 orang di Kecamatan A. Jadi, pernyataan 2 Salah.
• Banyaknya orang yang tidak aktif secara ekonomi di Kecamatan A adalah 1.800 = 4,5 kali banyak orang yang tidak aktif secara ekonomi di Kecamatan B. Jadi, pernyataan 3 Salah.

Soal no 7

Perbandingan angkatan kerja yang bekerja di Kecamatan A dengan yang bekerja atau menganggur dari kedua kecamatan adalah ….
(A)   1 : 2
(B)   3 : 8
(C)   5 : 8
(D)   15 : 38
(E)    23 : 38

Jawab: (D)

Jumlah angkatan kerja yang bekerja di Kecamatan A adalah 9.000 orang. Jumlah angkatan kerja yang aktif secara ekonomi (bekerja atau menganggur) dari kedua kecamatan adalah 14.400 + 8.400 = 22.800 orang, sehingga perbandingan yang dimaksud adalah 9.000 : 22.800 = 15 : 38.

Soal no 8

Dari semua angkatan kerja yang menganggur di kedua kecamatan, persentase yang tinggal di Kecamatan B adalah ___ %.

Jawab: 50%

Dari kedua kecamatan jumlah angkatan kerja yang menganggur adalah 8.400 orang dan 4.200 diantaranya berasal dari Kecamatan B.

Sehingga persentase yang tinggal di Kecamatan B adalah

Soal no 9

Jika seseorang dipilih secara acak dari kedua kecamatan, peluang orang yang terpilih bekerja atau menganggur adalah ….
(A)   ⁴²/₁₂₅
(B)   ⁷²/₁₂₅
(C)   ⁸³/₁₂₅
(D)   ¹¹⁴/₁₂₅
(E)   ¹¹⁷/₁₂₅

Jawab: (D)

Jumlah angkatan kerja yang aktif secara ekonomi (bekerja atau menganggur) dari kedua kecamatan adalah 14.400 + 8.400 = 22.800 orang. Jumlah angkatan kerja di dua kecamatan adalah 15.000 + 10.000 = 25.000, sehingga besar peluang orang yang dililih bekerja atau menganggur adalah

Soal no 10

Jika pada tahun 2023 terjadi kenaikan jumlah orang yang bekerja di Kecamatan A sebanyak 10% dari tahun sebelumnya, dengan asumsi populasi angkatan kerja dan orang yang tidak aktif secara ekonomi tetap, maka persentase pengangguran di Kecamatan A berkurang … %.
(A)   6
(B)   7
(C)   8
(D)   9
(E)   10

Jawab: (A)

Perubahan komposisi di Kecamatan A pada tahun 2023 adalah sebagai berikut.

Jadi, terjadi pengurangan orang yang menganggur sebanyak 6%.

Demikianlah tadi penjelasan pembahasan contoh soal PM UTBK SNBT 2024 dari halaman simulasi-tes.bppp.kemdikbud.go.id, terima kasih sudah mengunjungi idschool dot net. Semoga bermanfaat!

Baca Juga: Kumpulan Soal UTBK 2023 dan Pembahasannya