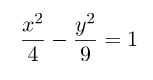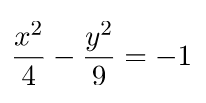Bentuk dari irisan kerucut dapat berupa hiperbola, bentuknya mirip dengan dua parabola yang dicerminkan. Salah satu pembahasan dalam materi hiperbola adalah kedudukan titik terhadap hiperbola. Kedudukan tersebut dapat meliputi titik di dalam hiperbola, titik pada hiperbola, dan titik di luar hiperbola. Melalui halaman ini akan diulas bagaiman cara menentuka kedudukan titik terhadap hiperbola dengan memanfaatkan persamaan umum hiperbola.
Sebuah titik yang terletak satu bidang dengan hiperbola akan mempunyai tiga kemungkinan kedudukan, yaitu titik di dalam parabola, titik pada parabola, atau titik di luar parabola. Ilustrasi tiga kemungkinan kedudukan titik terhadap hiperbola dapat dilihat seperti gambar di bawah.

Dengan melihat kedudukan titik pada hiperbola melalui gambar, akan secara mudah ditentukan kedudukan titik terhadap hiperbola. Namun, bagaimana jika yang diketahui hanya persamaan hiperbola dan letak koordinat sebuah titik? Bagaimanakah sobat idschool dapat mengetahui kedudukan titik pada parabola tersebut?

Baca Juga: Irisan Kerucut Hiperbola
Menentukan kedudukan titik terhadap hiperbola dengan cara menggambarkan hiperbola dari persamaan yang diketahui kemudian melihat letak titik yang diketahui koordinatnya, tentu bukan merupakan cara yang efektif.
Melalui halaman ini, sobat idschool akan belajar menentukan kedudukan titik terhadap hiperbola yang diketahui persamaannya dan sebuah titik yang diketahui letak koordinatnya. Pastinya, tanpa menggambarkannya terlebih dahulu pada bidang kartesius.
Table of Contents
Titik di dalam Hiperbola
Pembahasan pertama adalah mengetahui letak titik terhadap hiperbola untuk titik di dalam hiperbola. Sebuah titik dikatakan terletak di dalam hiperbola jika titik koordinat tersebut berada di area dalam lengkungan hiperbola.
Kriteria titik di dalam hiperbola dapat ditentukan melalui persamaan yang diberikan di bawah.

Contoh soal menentukan kedudukan titik terhadap hiperbola
Soal:
Selidikilah kedudukan titik (3, 1) terhadap hiperbola yang memiliki persamaan berikut.
Jawab:
Substitusi nilai x dan y, titik koordinat (3, 1) pada persamaan hiperbola.
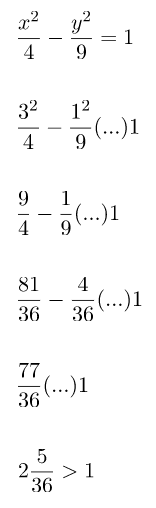
Berdasarkan perhitungan di atas, dapat disimpulkan bahwa titik (3, 1) berada di dalam hiperbola. Sesuai dengan kriteria kedudukan titik terhadap hiperbola untuk titik di dalam hiperbola. Untuk lebih meyakinkan sobat idschool, perhatikan letak titik terhadap hiperbola sesuai dengan soal yang berikan.

Baca Juga: Kedudukan Garis Terhadap Hiperbola
Titik pada Hiperbola
Ke dua adalah pembahasan mengenai letak titik terhadap hiperbola untuk titik pada hiperbola. Sebuah titik dikatakan terletak pada hiperbola jika titik koordinat tersebut berada garis lengkung hiperbola. Kriteria titik pada hiperbola dapat ditentukan melalui persamaan berikut.

Contoh soal menentukan kriteria titik pada hiperbola
Soal:
Selidikilah kedudukan titik (0, 3) terhadap hiperbola yang memiliki persamaan berikut.
Jawab:
Substitusi nilai x dan y, titik koordinat (0, 3), pada persamaan hiperbola.
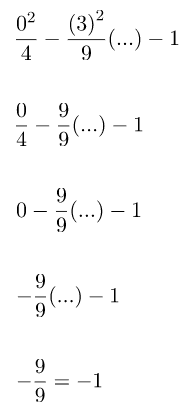
Berdasarkan perhitungan di atas, dapat disimpulkan bahwa titik (0, 3) berada pada hiperbola. Sesuai dengan kriteria kedudukan titik terhadap hiperbola untuk titik pada hiperbola. Untuk lebih meyakinkan sobat idschool, perhatikan letak titik terhadap hiperbola sesuai dengan soal yang berikan.

Terlihat bahwa letak titik berada pada lengkung hiperbola, bukan?
Baca Juga: Aplikasi Integral – Mencari Luas Daerah yang Dibatasi Kurva
Titik di Luar Hiperbola
Pembahasan berikutnya adalah mengetahui letak titik terhadap hiperbola untuk titik di luar hiperbola. Sebuah titik dikatakan terletak di luar hiperbola jika titik koordinat tersebut berada di luar area lengkungan hiperbola. Kriteria titik di luar hiperbola dapat ditentukan melalui persamaan yang diberikan di bawah.

Contoh soal menentukan kriteria titik di luar hiperbola
Selidikilah kedudukan titik (3, –1) terhadap hiperbola yang memiliki persamaan berikut.
Jawab:
Substitusi nilai x dan y, titik koordinat (3, –1) pada persamaan hiperbola.
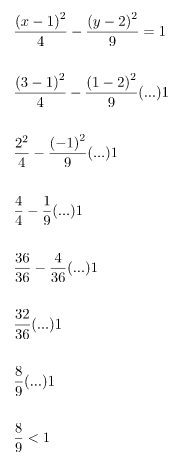
Berdasarkan perhitungan di atas, dapat disimpulkan bahwa titik (3, –1) berada di luar parabola. Sesuai dengan kriteria kedudukan titik terhadap hiperbola untuk titik di luar hiperbola. Untuk lebih meyakinkan sobat idschool, perhatikan letak titik terhadap hiperbola sesuai dengan soal yang berikan pada gambar di bawah.

Demikianlah pembahasan mengenai tiga kriteria untuk menentukan kedudukan titik terhadap hiperbola. Kesimpulan krtiteria untuk menentukan kedudukan titik terhadap hiperbola dapat dilihat pada tabel di bawah.

Sekian pembahasan mengenai kedudukan titik terhadap hiperbola. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Irisan Kerucut (Lingkaran, Elips, Parabola, Hiperbola)