Dalam materi trigonometri, ada rumus jumlah dan selisih dua sudut dan rumus sudut rangkap, selain itu terdapat juga rumus trigonometri sudut pertengahan. Rumus-rumus tersebut digunakan untuk menentukan nilai fungsi trigonometri suatu sudut (utamanya untuk bukan sudut istimewa) tanpa alat bantu hitung seperti kalkulator atau tabel. Contoh sudut yang termasuk sudut istimewa adalah 30o, 45o, 60o, 90o, dan lain sebagainya. Sedangkan contoh sudut yang bukan merupakan sudut istimewa adalah 75o, 105o, dan lain sebagainya.
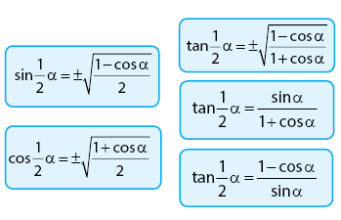
Rumus trigonometri sudut pertengahan meliputi fungsi sinus, cosinus, dan cotangan dengan besar sudut pertengahan (1/2α). Persamaan-persamaan dalam rumus trigonometri sudut pertengahan sesuai rumus-rumus berikut.
Kelima rumus fungsi trigonometri sudut pertengahan merupakan rumus identitas yang dapat dibuktikan. Bagaimana pembuktian dari persamaan rumus trigonometri sudut pertengahan? Bagaimana penggunaan rumus trigonometri sudut pertengahan? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah,
Table of Contents
Rumus Sinus Sudut Tengahan
Persamaan fungsi sinus dengan besar sudut 1/2α sesuai dengan identitas berikut.

Bukti:
Untuk membuktikan rumus sinus sudut pertengahan, sobat dapat menggunakan rumus cosinus sudut rangkap yang sudah dibuktikan sebelumnya yaitu Cos 2A = 1 ‒ 2 sin2A.
Misalkan A = 1/2α,
maka dapat diperoleh persamaan dan pembuktian rumus trigonometri sudut pertengahan untuk fungsi sinus seperti berikut.
cos 2(½α) = 1 ‒ 2 sin2(½α)
cos α = 1 ‒ 2 sin2(½α)
2 sin2(½α) = 1 ‒ cos α
sin2(½α) = 1 ‒ cos α/2
sin ½α = ± √(1 ‒ cos α/2) Terbukti
Baca Juga: Rumus Trignometri Sudut Rangkap
Contoh 1: Soal dan pembahasan penggunaan rumus trigonometri sudut pertengahan untuk fungsi sinus
Tentukan nilai dari sin 22,5o!
Pembahasan cara menentukan nilai 22,5o:
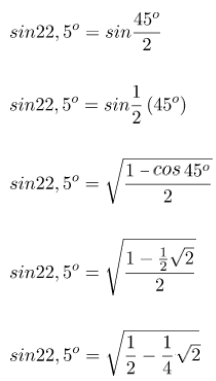
Baca Juga: Rumus Penjumlahan/Selisih Fungsi Sinus dan Cosinus
Rumus Cosinus Sudut Tengahan
Persamaan fungsi sinus dengan besar sudut 1/2α sesuai dengan identitas berikut.
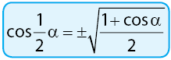
Bukti:
Untuk membuktikan rumus cosinus sudut pertengahan, sobat dapat menggunakan rumus cosinus sudut rangkap yang sudah dibuktikan sebelumnya yaitu Cos 2A = 2 Cos2A ‒ 1.
Misalkan A = 1/2α,
maka dapat diperoleh persamaan dan pembuktian rumus trigonometri sudut pertengahan untuk fungsi cosinus seperti berikut.
Cos 2(½α) = 2 Cos2 ½α ‒ 1
Cos α = 2 Cos2 ½α ‒ 1
2 Cos2 ½α = 1 + cos α
Cos ½α = 1 + cos α/2
Cos ½α = ±√(1 + cos α/2) Terbukti
Contoh 2: Soal dan pembahasan penggunaan rumus trigonometri sudut pertengahan untuk fungsi cosinus
Tentukan nilai dari Cos 22,5o!
Pembahasan:

Baca Juga: Fungsi Trigonometri dan Sudut Istimewa pada Trigonometri
Rumus Tangen Sudut Pertengahan
Ada 3 bentuk identitas rumus tangen dengan besar sudut ½α. Bentuk dan pembuktian dari tiga rumus trigonomteri sudut pertengahan untuk fungsi tangen diberikan seperti kedua ulasan di bawah
1) Rumus tangen sudut pertengahan bentuk pertama:
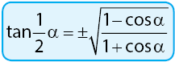
Bukti:
Untuk membuktikan rumus tangen sudut pertengahan, sobat dapat menggunakan rumus identitas untuk Sin ½α dan Cos ½α yang telah dibuktikan di atas.
Diketahui bahwa fungsi tangen: Tan α = Sin α/Cos α, sehingga dapat diperoleh persamaan dan penyelesaian seperti cara berikut.

Terbukti untuk fungsi tangen sudut pertengahan bentuk pertama.
2) Rumus tangen sudut pertengahan kedua:
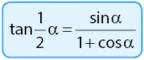
Bukti:
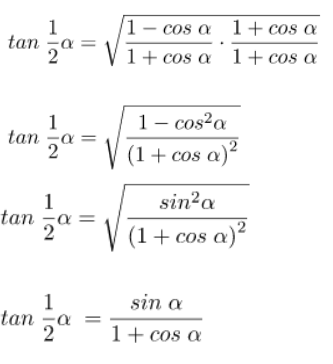
Terbukti untuk fungsi tangen sudut pertengahan bentuk kedua.
3) Rumus tangen sudut pertengahan ketiga:
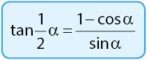
Bukti:

Terbukti untuk fungsi tangen sudut pertengahan bentuk ketiga.
Contoh 3: Soal dan pembahasan penggunaan rumus trigonometri sudut tengahan untuk fungsi tangen
Tentukan nilai dari Tan 22,5o!
Penyelesaian:


Demikianlah tadi ulasan rumus trigonometri sudut pertengahan yang meliputi fungsi sinus, cosinus, dan cotangen. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Rumus Trigonometri Sudut Rangkap