Pertidaksamaan kuadrat adalah fungsi kuadrat yang memiliki hubungan lebih besar atau lebih kecil. Pada persamaan kuadrat memiliki satu bentuk umum yaitu ax2 + bx + c = 0. Kedua ruas dihubungkan oleh tanda sama dengan (=). Sementara pada pertidaksamaan kuadrat kedua ruas dapat dihubungkan oleh > , ≥, <, ≤, atau ≠.
Contoh pertidaksamaan kuadrat adalah 2x2 – 7x + 6 ≤ 0. Himpunan penyelesaian pertidaksamaan kuadrat adalah semua nilai x yang memenuhi pertidaksamaan tersebut. Lebih lanjut cara menentukan himpunan penyelesaian pertidaksamaan kuadrat ada di bawah.
Daftar isi:
Baca Juga: Cara Menentukan Persamaan Grafik Fungsi Kuadrat
Langkah-langkah menentukan himpunan pertidaksamaan kuadrat
Bentuk umum pertidaksmaan kuadrat meliputi ax2 + bx + c ≥ 0; ax2 + bx + c > 0; ax2 + bx + c < 0; ax2 + bx + c ≤ 0; atau ax2 + bx + c ≠ 0. Setiap nilai x yang memenuhi pertidaksamaan merupakan himpunan penyelesaiannya.
Untuk menentukan himpunan penyelesaiannya dapat mengikuti langkah-langkah berikut.
- Menentukan akar-akar persamaan.
- Membuat garis bilangan, batasnya menggukan akar-akar hasil nomor 1. Diperoleh beberapa daerah yang dibatasi oleh akar-akar persamaan.
- Menentukan daerah-daerahnya bernilai positif atau negatif. Cara menggunakan titik uji yang dimasukkan ke pertidaksamaan.
- Menentukan daerah yang sesuai dengan bentuk pertidaksamaan dan membentuk himpunan penyelesaian yang sesuai dengan pertidaksamaan.
Baca Juga: Persamaan dan Pertidaksamaan Linear Satu Variabel
1) Menentukan akar-akar persamaan
Langkah pertama untuk menentukan himpunan penyelesaian pertidaksamaan kuadrat adalah menentukan akar-akar persamaannya. Misalkan diberikan pertidaksamaan f(x) ≤ 0, maka dicari akar-akar yang memenuhi persamaan f(x) = 0. Cara ini dikenal dengan mengambil harga nol dari pertidaksamaan.
Untuk pertidaksamaan ax2 + bx + c ≤ 0 memiliki bentuk persamaan harga nol ax2 + bx + c = 0. Kemudian lakukan pemfaktoran untuk mendapatkan nilai x yang menjadi akar-akarnya. Cara melakukan pemfaktoran bentuk aljabar biasanya sudah diajarkan di bangku SMP.
2) Menentukan garis bilangan dan daerahnya
Misalkan akar-akar yang memenuhi persamaan ax2 + bx + c = 0 adalah a dan b. Nilai a dan b akan membagi garis bilangan menjadi tiga daerah.
Pertama adalah daerah di kiri nilai a, daerah kedua berada di antara nilai a dan b. Serta daerah ketiga adalah daerah di kanan nilai b.
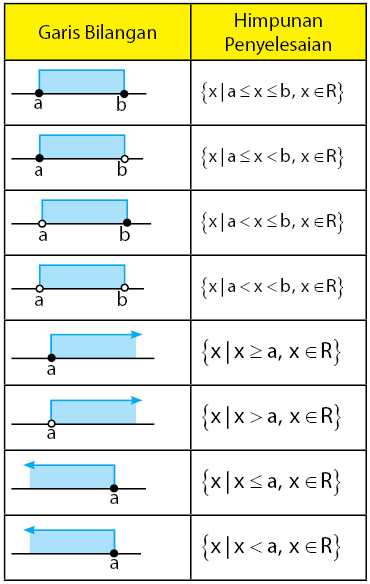
Gunakan bulatan tidak penuh untuk menandai akar-akar berasal dari pertidaksamaan lebih dari (>) atau kurang dari (<). Gunakan bulatan penuh untuk akar-akar yang berasal dari pertidaksamaan kurang dari sama dengan (≤) atau lebih dari sama dengan (≥).

3) Menentukan Nilai Positif/Negatif Daerahnya
Berikutnya adalah menentukan nilai positif/negatif dari masing-masing daerahnya. Caranya dengan mengambil sembarang titik dari salah satu daerah. TIPS: ambil nilai x = 0 untuk mempermudah perhitungan!
Substitusi nilai x ke persamaan f(x). Apakah menghasilkan nilai negatif atau positif. Kemudian beri tanda yang sesuai pada daerah hasil titik uji. Untuk daerah yang diselingi batas akar akan memiliki tanda yang sebaliknya.

Namun ada pengecualian ketika daerah dibatasi oleh akar kembar. Nilai positif/negatif dari daerah mengikuti nilai positif/negatid dari daerah sebelahnya. Perhatikan ilustrasi pada gambar di bawah.

4) Menentukan daerah dan himpunan penyelesaian
Terakhir hanya perlu menentukan daerah yang sesuai pertidaksamaannya. Ambil daerah negatif jika bentuk pertidaksamaannya f(x) < 0 atau f(x) ≤ 0. Ambil daerah positif jika bentuk pertidaksamaannya adalah f(x) > 0 atau f(x) ≥ 0.
Selanjutnya bentuk himpunan penyelesaian sesuai dengan daerah yang memenuhi. Bentuk umum himpunan penyelesaiannya pertidaksamaan terdapat pada tabel di bawah.
Baca Juga: Cara Menentukan Persamaan Kuadrat Baru
Contoh Soal dan Pembahasan
Beberapa soal pertidaksamaan kuadrat dan pembahasannya ada di bawah.
Contoh 1 – Soal Pertidaksamaan Kuadrat
Himpunan penyelesaian yang memenuhi pertidaksamaan kuadrat x2 – x – 12 ≥ 0 adalah ….
A. { x ≤ -3}
B. { x ≤ 4}
C. { x ≤ -3 atau x ≥ 4}
D. {x ≤ -3}
E. { -3 ≤ x ≤ 4}
Pembahasan:
Harga nol dari pertidaksamaan kuadrat x2 – x – 12 ≥ 0 adalah x2 – x – 12 = 0.
Pemfaktoran x2 – x – 12 = 0:
x2 – x – 12 = 0
(x + 3)(x – 4) = 0
Diperoleh dua nilai x yaitu:
x + 3 = 0
x = -3
Atau,
x – 4 = 0
x = 4
Nilai akar-akarnya membagi garis bilangan menjadi tiga daerah. Pertama adalah daerah di kiri x = -3, kedua adalah daerah antara x = -3 dan x = 4, dan terakhir adalah daerah di kanan x = 4.

Ambil titik uji x = 0, kemudian substitusikan nilainya ke persamaan kuadrat. Untuk x = 0, maka nilai dari persamaan kuadrat menjadi 02 – 0 – 12 = -12. Sehingga daerah yang memuat angka nol memiliki daerah yang bernilai negatif.
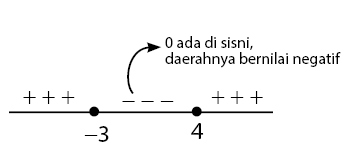
Daerah yang memuat angka nol bertanda negatif. Maka dua daerah di sampingnya bertanda positif.
Bentuk pertidaksamaan pada soal adalah x2 – x – 12 ≥ 0. Sehingga himpunan penyelesaian yang memenuhi adalah daerah yang bernilai positif.

Jadi himpunan penyelesaiannya adalah x ≤ – 3 atau x ≥ 4.
Jawaban: C
Baca Juga: Pertidaksamaan Nilai Mutlak
Contoh 2: Soal Pertidaksamaan Kuadrat
Himpunan penyelesaian dari pertidaksamaan x2 – 5x – 14 ≤ 0, x ϵ R adalah ….
A. {x | x < 2 atau x > 7, x ϵ R}
B. {x | x < -2 atau x > 7, x ϵ R}
C. {x | x < -7 atau x > -7, x ϵ R }
D. {x | -2 < x < 7, x ϵ R}
E. {x | – 2 ≤ x ≤ 7, x ϵ R}
Pembahasan:
Harga nol dari pertidaksamaan x2 – 5x – 14 ≤ 0 adalah x2 – 5x – 14 = 0.
Pemfaktoran:
x2 – 5x – 14 = 0
( x – 7)(x + 2) = 0
Selanjutnya dapat diperoleh dua nilai x, yaitu:
x – 7 = 0
x = 7
Atau,
x + 2 = 0
x = -2
Dua nilai x akan membagi garis bilangan menjadi tiga seperti berikut.

Selanjutnya, akan diselidiki nilai dari masing-masing daerah. Ambil titik uji x = 0, kemudian substitusikan nilainya ke persamaan kuadrat.
Untuk x = 0 maka pada persamaan x2 – 5x – 14 memiliki nilai 02 – 5(0) – 14 = = -14 . Untuk x = 0 menghasilkan nilai negatif, sehingga daerah yang memuat angka nol, daerahnya adalah negatif.
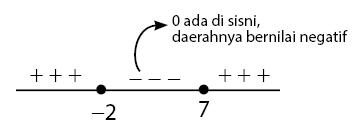
Pertidaksamaan kuadrat yang diberikan adalah x2 – 5x – 14 ≤ 0. Maka himpunan penyelesaian yang memenuhi adalah daerah negatif yaitu daerah antara x = -2 atau x = 7 (-2 ≤ x ≤ 7).

Jadi himpunan penyelesaiannya adalah {x | – 2 ≤ x ≤ 7, x ϵ R}.
Jawaban: E
Demikianlah tadi ulasan materi pertidaksamaan kuadrat dan himpunan penyelesaiannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Himpunan penyelesaian pertidaksamaan yang akarnya kembar gimana kk?
Halo Syfa, secara umum pengerjaannya sama seperti yang diulas di atas yaaa. Perlu diketahui bahwa pada akar kembar daerah bertanda +/- bisa tidak selang-seling bergantian, untuk menentukannya bisa diuji melalui subsitusi sebuah titik pada daerah ke fungsinya. Dari sana dapat diketahui apakah daerah bernilai positif atau negatif.
kak mau nanya cara menghitung himpunan dari garis bilangannya saja gimana ya?
Halo Haical, bisa dikasih contoh seperti apa soalnya?
X2 – 4 < 0 =
Harga nol: x^2 – 4 = 0
Faktorkan: (x – 2)(x + 2) = 0
Akar-akar: x1 = 2 atau x2 = -2
Garis bilangan: +++ (-2) — (2) +++
.
Bentuk pertidaksamaan adalah kurang dari sama dengan, sehingga himpunan penyelesaiannya adalah daerah yang menghasilkan nilai negatif
.
Daerah yang selalu bernilai negatif berada di antara nilai -2 dan 2. Jadi, himpunan penyelesaiannya adalah HP = {x | -2 <= x <= 2 } . Semoga bisa membantu :)
Kak mau nanya kalau x1 sama x2 nya positif berarti ititk koordinatnya ke kanan semua ?
Halo Aryo, nilai akar-akar yang diperoleh positif tidak menunjukkan bahwa daerah yang memenuhi di sebelah kanan. Setelah mendapatkan nilai x1 dan x2 kamu akan mendapatkan daerah-daerah yang dipisah oleh titik tersebut. Selanjutnya, kamu perlu melakukan uji daerah tersebut termasuk daerah yang menghasilkan nilai positif atau negatif terlebih dahulu. Himpunan penyelesaian diambil setelah melakukan uji daerah, sesuai yang disyaratkan.
Kak mau tanya, cara menentukan lebih besar dan lebih kecil suatu himpunan penyelesaian itu gimana ya?
Halo Aura, kamu perlu melakukan uji daerah tersebut termasuk daerah yang menghasilkan nilai positi atau negatif terlebih dahulu. Setelah itu, himpunan penyelesaian dapat diperoleh dari sana.