Cara Menggambar Grafik Fungsi Eksponen dalam 4 Langkah

Grafik fungsi eksponen adalah kurva mulus yang dibentuk dari suatu persamaan bilangan berpangkat. Bentuk grafik fungsi eksponen berupa sebuah garis lengkungan yang tidak berhingga. Cara menggambar grafik fungsi eksponen pada dasarnya cukup mudah yang dapat dilakukan diperoleh melalui empat langkah. Bentuk grafik fungsi ekponen dapat berupa kurva monoton naik atau kurva monoton turun.

Selanjutnya, bagaimana bentuk grafik fungsi eksponen? Apa saja langkah-langkah atau proses yang dilakukan pada cara menggambar grafik fungsi eksponen? Sobat idschool dapat mencari tahu bagaimana cara menggambar graafik fungsi eksponen melalui ulasan di bawah.

Table of Contents

• 4 Langkah pada Cara Menggambar Grafik Fungsi Eksponen
• Contoh Cara Menggambar Grafik Fungsi Eksponen
  • #1 Pertama: ambil beberapa titik absis (x) secara sembarang
  • #2 Kedua: Tentukan nilai ordinat (y) sekaligus titik koordinatnya
  • #3 Ketiga: tentukan letak titik koordinat yang diperoleh dalam bidang kartesius
  • #4 Keempat: Hubungkan titik-titik yang diperoleh sehingga membentuk kurva mulus
• Contoh Soal dan Pembahasan
  • Contoh 1 – Soal Grafik Fungsi Eksponen
  • Contoh 2 – Soal Grafik Fungsi Eksponen
  • Contoh 3 – Soal Menentukan Grafik Fungsi Eksponen

4 Langkah pada Cara Menggambar Grafik Fungsi Eksponen

Kemampuan dasar yang dibutuhkan agar dapat menggambar grafik fungs eksponen adalah melakukan perhitungan perpangkatan dan menentukan letak titik koordinat. Perhitungan perpangkatan dilakukan dengan cara mengalikan suatu bilangan sebanyak bilangan pangkatnya. Secara umum, perpankatan bilangan aⁿ = a × a × … × a (perkalian a sebanyak n kali). Misalnya cara menghitung nilai 2⁵ sama dengan perkalian bilangan 2 sebanyak lima kali, 2⁵ = 2 × 2 × 2 × 2 = 32.

Letak titik koordinat pada bidang kartesius secara umum dinyatakan dalam (x, y). Di mana x untuk arah mendatar/horizontal dan y untuk arah tegak/vertikal. Jadi letak (x, y) berbeda dengan (y, x), sehingga sobat idschool perlu memperhatikan mana nilai x mana nilai y

Setidaknya ada empat langkah yang dilakukan pada cara menggambar grafik fungsi eksponen. 4 langkah pada cara menggambar grafik fungsi eksponen Cara mendapatkan grafik fungsi eksponen y = b^x secara umum diberikan seperti daftar berikut.

4 Langkah pada cara menggambar grafik fungsi eksponen:

1. Mengambil sembarang nilai absia atau titik x
2. Mentukan nilai y melalui persamaan y = b^x, di mana b merupakan suatu bilangan. Sehingga dpat diperoleh titik koordinat (x, y)
3. Menentukan letak setiap titik-titik koordinat yang di dapat pada bidang kartesius
4. Menghubungkan titik-titik koordinat pada bidang kartesius sehingga diperoleh kurva yang merupkan grafik fungsi y = b^x

Baca Juga: Pengertian Eksponen (Bilangan Berpangkat)

Contoh Cara Menggambar Grafik Fungsi Eksponen

Sobat idschool dapat melihat bagaimana proses atau cara menggambar grafik fungsi eksponen melalui sebuah contoh di bawah.

Cara menggambar grafik fungsi eksponen y = 2^x dapat dilakukan seperti pada langkah-langkah berikut.

#1 Pertama: ambil beberapa titik absis (x) secara sembarang

Dalam mengambil titik absis (x) usahakan memiliki nilai yang memuat bilangan negatif dan positif yang urut. Pemilihan nilai x tersebut akan membantu mendapatkan grafik fungsi eksponen yang baik. Pada soal ini, misalnya ambil nilai absis x = –2, –1, 0, 1, 2, dan 3.

#2 Kedua: Tentukan nilai ordinat (y) sekaligus titik koordinatnya

• Untuk x = –2:
  Nilai y = 2^(–2) = ¹/₄
  Titik koordinatnya (–2, ¹/₄)

• Untuk x = –1:
  y = 2^(–1) =¹/₂
  Titik koordinatnya (–1, ¹/₂)

• Untuk x = 0:
  y = 2⁰ = 1 → Ingat!!! Semua bilangan yang dipangkatkan dengan 0 hasilnya adalah 1 (satu).
  Titik koordinatnya (0, 1)

• Untuk x = 1:
  y = 2¹ = 2
  Titik koordinatnya (1, 2)

• Untuk x = 2:
  y = 2² = 2 × 2 = 4
  Titik koordinatnya (2, 4)

• Untuk x = 3:
  y = 2³ = 2 × 2 × 2 = 8
  Titik koordinatnya (3, 8)

Baca Juga: Invers Eksponen – Logaritma (Definisi dan Sifat – Sifat)

#3 Ketiga: tentukan letak titik koordinat yang diperoleh dalam bidang kartesius

Keenam titik koordinat yang diperoleh adalah (–2, ¹/₄); (–1, ¹/₂); (0, 1); (1, 2); (2, 4); dan (3, 8). Letak keenam titik koordinat yang diperoleh pada bidang koordinat dapat dilihat seperti gambar di bawah.

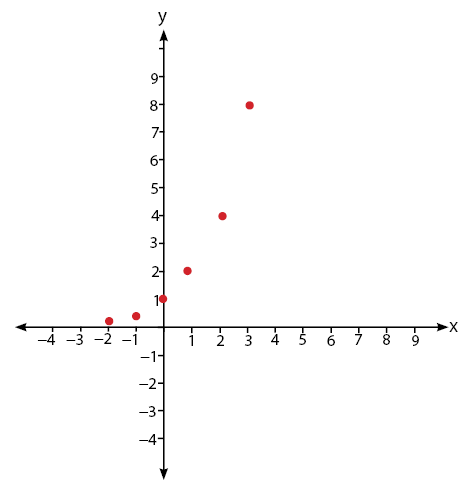
#4 Keempat: Hubungkan titik-titik yang diperoleh sehingga membentuk kurva mulus

Proses cara menggambar grafik fungsi eksponen hanya tinggal menghubungkan titik-titik koordinatnya. Diperoleh gambar fungsi eksponen dapat dilihat seperti gambar berikut.

Baca juga: Cara Menggambar Grafik Fungsi Logaritma

Bagaimana, mudah bukan cara menggambar grafik fungsi eksponen? Untuk menambah pemahaman sobat idschool, simak contoh soal bahasan grafik fungsi eksponen yang diberikan di bawah.

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan grafik fungsi eksponen di atas. Setiap soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Soal Grafik Fungsi Eksponen

Perhatikan gambar di bawah!

Persamaan grafik fungsi di atas adalah ….
A. y = x³
B. y = 3^x
C. y = x^(1/3)
D. y = (¹/₃)^x
E. y = 3^–x

Pembahasan:
Berdasarkan grafik pada soal dapat diketahui bahwa ada dua titik kunci yaitu (2, 9) dan (0, 1). Di mana nilai y = 9 = 3² dan y = 1 = 3⁰, dengan pangkat dari bilangan tiga merupakan nilai x = 2 dan x = 0. Perhatikan bahwa bilangan 3 dipangkatkan dengan nilai absis (x) menghasilkan nilai y.

Sehingga dapat diperoleh kesimpulan bahwa persamaan y memenuhi persamaan y = 3^x. Jadi, persamaan grafik fungsi pada soal adalah y = 3^x.

Jawaban: B

Contoh 2 – Soal Grafik Fungsi Eksponen

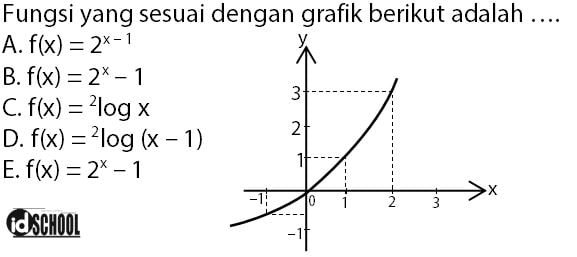
Pembahasan:
Grafik dari persamaan y = 2^x akan menghasilkan titik-titik koordinat: …; (–2, ¹/₄); (–1, ¹/₂); (0, 1) ; (1, 2); (2, 4); … dan seterusnya. Sedangkan titik-titik koordinat pada grafik di soal diketahui (–1, –¹/₂); (0, 0); (1, 1); dan (2, 3).

Perhatikan bahwa untuk nilai absis (x) yang sama, nilai ordinat (y) berkurang 1. Sehingga dapat diperoleh kesimpulan bahwa grafik fungsi eksponen pada soal merupakan grafik y = 2^x yang bergeser satu satuan ke bawah. Atau fungsi dari grafik eksponen pada soal adalah y = 2^x – 1.

Jawaban: B

Contoh 3 – Soal Menentukan Grafik Fungsi Eksponen

Perhatikan gambar berikut!

Persamaan grafik fungsi di atas adalah ….
A. y = 3×2^x+2
B. y = 3×2^x+1
C. y = 3×2^x
D. y = 3×2^x−1
E. y = 3×2^x−2

Pembahasan:
Dari keterangan grafik eksponen yang diberikan pada soal dapat diperoleh informasi bahwa terdapat titik potong di titik (0, 6). Artinya, ketika nilai x = 0 maka nilai ordinatnya akan sama dengan 6 (y = 6).

Untuk menentukan persamaan dari grafik eksponen tersebut, kita perlu melihat pilihan ganda yang diberikan agar lebih mudah. Semua pilihan ganda memuat bilangan berpangkat 2^x.

Titik potong grafik eksponen y = 2^x dengan sumbu y terdapat di titik (0, 1). Agar ketika x = 0 menghasilkan nilai y = 6 maka nilai x perlu ditambah 1, sehingga menjadi y = 2^x+1. Namun persamaan tersebut belum menghasilkan nilai y = 6, melainkan y = 2.

Agar nilai ordinat menjadi y = 6 hasilnya perlu dikalikan 3. Sehigga persamaan menjadi y = 2^x+1 × 3, dari persamaan tersebut ketika x = 0 akan menghasilkan nilai y = 6.

Jadi, persamaan grafik fungsi di atas adalah y = 3×2^x+1.

Jawaban: B

Demikianlah tadi ulasan cara menggambar grafik fungsi eksponen yang dapat dilakukan melalui empat langkah. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Contoh Soal UN SMA IPA – Invers, Komposisi, dan Grafik Fungsi