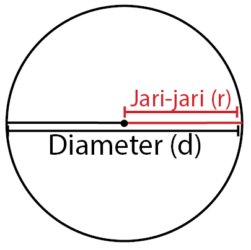
Rumus tabung terdiri dari rumus volume dan luas tabung. Rumus volume tabung adalah V tabung = 2π × r2 × t dan rumus luas tabung adalah L tabung = 2π × r × (r + t). Keterangan: r = jari-jari lingkaran alas atau tutup tabung dan t = tinggi tabung.
Rumus volume tabung digunakan untuk menghitung isi atau kapasitas ruangan dari bangun ruang berbentuk tabung. Sedangkan luas tabung digunakan untuk menghuitung seluruh luas sisi-sisi yang membentuk bangun tabung.
Sebagai contoh, sebuah tabung memiliki jari-jari lingkaran alas 7 cm dan tinggi tabung 10 cm. Volume tabung tersebut adalah V tabung = 2π × 72 × 10 = 980π cm3 dan luas tabung tersebut adalah L tabung = 2π × 7 × (7 + 10) = 238π cm2. Detail ulasan dibawah akan menjelaskan lebih banyak mengenai cara menghitung rumus volume tabung dan luas permukaan tabung.
Daftar isi:
Bentuk Tabung dan Jaring-Jaringnya
Tabung adalah bangun ruang yang memiliki tiga sisi. Dua sisi tabung berbentuk lingkaran yang merupakan tutup dan alas tabung. Satu sisi tabung lainnya adalah selimut tabung yang berbentuk persegi panjang.
Gambar tabung beserta jaring-jaring dan keterangannya
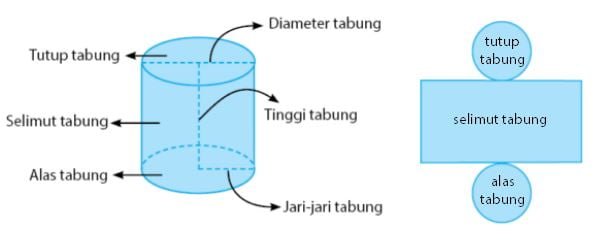
Sebuah tabung memiliki volume dan luas permukaan yang dapat dihitung menggunakan nilai jari-jari alas dan tinggi tabungnya. Bagaimana cara menghitung volume dan luas permukaan dari sebuah tabung akan menjadi pembahasan selanjutnya.
Baca Juga: Rumus Volume dan Luas Permukaan Limas
Rumus Volume Tabung
Volume tabung menunjukkan isi dari bangun ruang berbentuk tabung. Misalnya, sebuah drum berbentuk tabung dapat menampung 100 liter. Besar 100 liter air pada tabung tersebut mewakili besar volume tabung tersebut.
1) Rumus Volume Tabung Penuh
Besar daya tampung atau isi/volume bangun ruang berbentuk tabung diperngaruhi oleh panjang jari-jari (r) dan tinggi tabung (t). Rumus untuk menghitung seluruh isi yang dapat dimuat oleh tabung dinyatakan dalam persamaan di bawah.

- Keterangan:
- π = 3,14 atau π = 22/7
- r = jari-jari lingkaran alas atau tutup tabung
- t = tinggi tabung
Cara menghitung rumus volume tabung penuh:
Sebuah bak penampungan air berbentuk tabung memiliki jari-jari lingkaran alas 70 cm dan tingginya 3,5 meter. Jika bak tersebut terisi penuh oleh air, volume air yang termuat dalam tabung tersebut adalah ….
Jawab:
Dari soal diberikan beberapa nilai seperti berikut.
- Diketahui:
- Jari-jari lingkaran alas tabung: r = 70 cm = 0,7 m
- Tinggi tabung: t = 3,5 meter
Menghitung rumus volume tabung:
V tabung = 5,39 m3 = 5.390 liter
Baca Juga: Rumus Luas Permukaan dan Volume Setengah Bola
2) Rumus n per bagian Volume Tabung
Pada beberapa permasalahan, bagian isi tabung tidak terisi penuh. Isi sebuah tabung dapat hanya terdiri dari setengah bagian, satu per empat bagian, atau n per bagian.
Untuk menghitung volume n per bagian tabung dapat menggunakan persamaan berikut.

- Keterangan:
- π = 3,14 atau π = 22/7
- r = jari-jari lingkaran alas/tutup tabung
- t = tinggi tabung
Cara menghitung n per bagian volume tabung:
Soal:
Sebuah bak penampungan air berbentuk tabung yang memiliki jari-jari lingkaran alas 150 cm dan tinggi 3,5 m. Diketahui bak tersebut terisi 2⁄3 oleh air, volume air yang ada dalam tabung tersebut adalah ….
Jawab:
Dari keterangan yang diberikan pada soal terdapat beberapa informasi nilai berikut.
- Diketahui:
- Jari-jari lingkaran alas: r = 150 cm = 1,5 m
- Tinggi tabung: t = 3,5 m
- Isi tabung = 2⁄3 bagian
Menghitung volume 2/3 bagian tabung:
Jadi, volume air yang ada dalam tabung tersebut adalah 16.5 m3 = 16.500 liter.
Rumus Luas Tabung
Luas tabung seluruhnya sama dengan jumlah luas sisi alas tabung, luas sisi tutup tabung, dan luas selimut tabung. Luas alas dan tutup tabung berbentuk lingkaran sehingga luasnya dapat dihitung menggunakan rumus lingkaran yaitu L = 2 × π × r2.
Untuk luas selimut tabug berbentuk persegi panjang dengan ukuran panjang sama dengan keliling lingkaran ( 2 × π × r) dan lebarnya sama dengan tinggi tabung. Sehingga luas selimut tabung dapat dihitung menggunakan persamaan L = 2 × π × r × t.
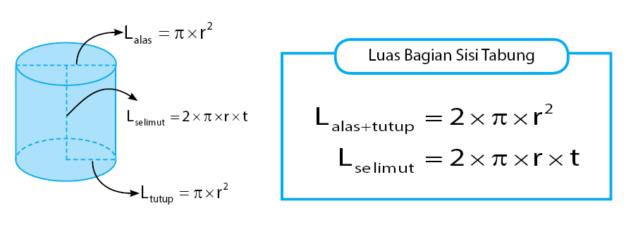
1) Luas Seluruh Permukaan Tabung
Luas permukaan tabung merupakan penjumlahan dari semua sisi-sisi tabung. Tabung memiliki tiga sisi yaitu dua sisi berbentuk lingkaran (alas dan tutup) dan satu sisi berbentuk persegi panjang (selimut tabung). Jadi luas permukaan tabung seluruhnya dapat diperoleh dengan menjumlahkan ketiga sisi tersebut.
Sebuah tabung yang memiliki jari-jari lingkaran alas r dan tinggi tabung t memiliki rumus luas seluruh permukaan tabung L = 2π × r2 + 2π × r × t = 2π × r (r + t).

- Keterangan:
- π = 3,14 atau π = 22/7
- r = jari-jari lingkaran alas/tutup tabung
- t = tinggi tabung
Cara menghitung luas permukaan tabung:
Soal:
Diketahui sebuah tabung berdiameter 20 cm dengan tinggi tabung adalah 36 cm. Berapakah luas seluruh permukaan tabung tersebut?
Jawab:
Dari keterangan yang diberikan pada soal dapat diperoleh beberapa nilai seperti berikut.
- Diketahui:
- Diameter tabung: d = 20 cm
Jari-jari tabung: r = d : 2 = 20 : 2 = 10 cm - Tinggi tabung: t = 36 cm
- Diameter tabung: d = 20 cm
Menghitung luas tabung:
L tabung = 2 × π × r × ( r + t )
= 2 × 3,14 × 10 × (10 + 36)
= 2 × 3,14 × 10 × 46 = 2.888,8 cm2
Baca Juga: Rumus Luas Permukaan dan Volume Kerucut
2) Luas Permukaan Tabung Tanpa Tutup
Pada tabung tanpa tutup, bagian sisi yang membatasi tabung terdiri dari alas dan selimut tabung. Sehingga, rumus luas permukaan tanpa tutup yang memiliki ukuran jari-jari alas r dan tinggi tabung t adalah L tabung tanpa tutup = π × r × (r + 2t).
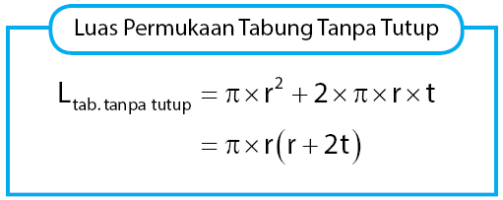
- Keterangan:
- π = 3,14 atau π = 22/7
- r = jari-jari alas/tutup tabung
- t = tinggi tabung
Cara menghitung luas tabung tanpa tutup:
Soal:
Diketahui sebuah tabung berdiameter 20 cm dengan tinggi tabung adalah 36 cm. Berapakah luas seluruh permukaan tabung tersebut tanpa tutup?
Jawab:
Dari keterangan yang diberikan pada soal dapat diperoleh beberapa informasi nilai berikut.
- Diketahui:
- Diameter tabung: d = 20 cm
Jari-jari tabung: r = d : 2 = 20 : 2 = 10 cm - Tinggi tabung: t = 36 cm
- Diameter tabung: d = 20 cm
Menghitung luas tabung:
L tabung = π × r × (r + 2t)
= 3,14 × 10 × (10 + 2 × 36)
= 31,4 × (10 + 72) = 31,4×82 = 2574,8 cm2
Baca Juga: Rumus Volume dan Luas Permukaan Prisma
- Kotak Ingat!!
- Gunakan π = 3,14 saat r = 10 atau kelipatannya
- Gunakan π = 22/7 saat r = 7 atau kelipatannya
Contoh Soal dan Pembahasan
Pembahasan soal volume dan luas tabung ada di bawah.
Contoh Soal 1
Untuk menghitung luas tabung yang berjari-jari a dan tinggi tiga kali jari-jari dapat menggunakan rumus ….
A. 3πa2
B. 4πa2
C. 8πa2
D. 9πa2
Pembahasan:
Dari infomrasi yang diberikan pada soal dapat diketahui beberapa nilai berikut.
- Diketahui:
- Jari-jari lingkaran alas tabung: r = a
- Tinggi tabung: t = 3×r = 3a
Menentukan rumus luas seluruh permukaan tabung:
L tabung = 2π × r × (r + t)
L tabung = 2π×a×(a + 3a) = 2π×a×4a = 8πa2
Jadi. luas tabung dengan jari-jari a dan tinggi tiga kali jari-jari adalah 8πa2.
Jawaban: C
Contoh Soal 2
Volume suatu tabung dengan panjang jari-jari alas 35 cm dan tinggi 12 cm adalah ….
A. 13.200 cm3
B. 35.500 cm3
C. 46.200 cm3
D. 50.400 cm3
Pembahasan:
Dari keterangan yang diberikan pada soal dapat diperoleh informasi beberapa nilai berikut.
- Diketahui:
- Jari-jari lingkaran alas tabung: r = 35
- Tinggi tabung: t = 12 cm
Cara menghitung rumus volume tabung: V tabung = π × r2 × t
V tabung = 22 × 5 × 35 × 12 = 46.200 cm3
Jadi, volume suatu tabung dengan panjang jari-jari alas 35 cm dan tinggi 12 cm adalah 46.200 cm3.
Jawaban: C
Sekian pembahasan mengenai rumus tabung yang meliputi rumus volume tabung, rumus luas seluruh permukaan tabung, dan rumus luas permukaan tabung tanpa tutup. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.