Rumus volume kubus adalah V kubus = s3 = s × s × s. Dan rumus luas permukaan kubus adalah L kubus = 6 × s2 = 6 × s × s. Nilai s pada rumus volume dan luas permukaan kubus adalah panjang rusuk kubus.
Sebagai contoh, diketahui sebuah kubus mempunyai panjang rusuk 10 satuan. Volume kubus tersebut adalah 1.000 satuan volume dan luas permukaannya adalah 600 satuan volume. Satuan volume yang digunakan adalah meter kubik (m3), sentimeter kubik (cm3), liter (dm3), cc, atau satuan volume lainnya.
Detail cara menghitung volume kubus dan luas permukaannya ada di bawah.
Daftar isi:
Bagian-Bagian Kubus
Kubus adalah salah satu bangun tiga dimensi yang memiliki 3 pasang persegi. Sehingga, ada enam persegi dalam sebuah kubus. Setiap persegi pada kubus akan sejajar atau berpotongan tegak lurus.
Kubus memiliki 12 rusuk, 8 titik sudut, 12 diagonal sisi, 4 diagonal ruang, dan 4 bidang diagonal. Setiap rusuk memiliki panjang yang sama. Kubus yang memiliki panjang rusuk s akan memiliki panjang diagonal sisi s√2 dan panjang diagonal ruang s√3.
Bagian-bagian penyusun kubus terdapat pada gambar berikut.

Bagian-bagian penyusun kubus:
| Nama Bagian | Banyaknya | Keterangan |
| Titik sudut | 8 | A, B, C, D, E, F, G, H |
| Bidang sisi | 12 | ABCD, EFGH, ADHE, BCGF, ABFE, DCGH |
| Rusuk | 12 | AB, BC, CD, DA, EF, FG, GH, HE, AE, BF, CG, DH |
| Diagonal sisi | 12 | AF, BE, BG, CF, CH, DG, AH, DE, AC, BD, EG, HF |
| Diagonal ruang | 12 | AG, CE, HB, DF |
| Bidang diagonal | 6 | ACGE, BDHF, EFCD, ABGH, BCHE, ADGF |
Baca Juga: Rumus Volume dan Luas Permukaan Limas
Rumus Kubus
Rumus volume dan luas permukaannya beserta contoh cara menghitungnya ada pada keterangan di bawah.
1) Volume Kubus
Secara umum, volume bangun ruang sama denga luas alas × tinggi. Luas alas berbebtnuk persegi, sehingga luas alas sama dengan panjang rusuk × rusuk. Tinggi kubus sama dengan panjang rusuknya.
Sehingga, sebuah kubus yang memiliki panjang rusuk s memiliki volume V = s × s × s = s3.

Cara menghitung volume kubus
Soal:
Sebuah kubus mempunyai panjang rusuk 3 cm. Tentukan volumenya!
Jawab:
Dari soal diberikan informasi panjang sisi kubus adalah s = 3 cm.
Menghitung volume:
V = s3 = s × s × s
V = 3 × 3 × 3 = 27 cm3
Jadi volume kubus tersebut adalah 27 cm3.
2) Luas permukaan kubus
Luas permukaan suatu bangun ruang sama dengan jumlah luas bidang sisi yang membentuknya. Kubus memiliki enam buah bidang sisi persegi. Luas sebuah persegi sama dengan panjang rusuk × rusuk.
Sehingga, rumus luas permukaan kubus yang memiliki panjang rusuk s adalah L kubus = 6 × s × s = 6 × s2.
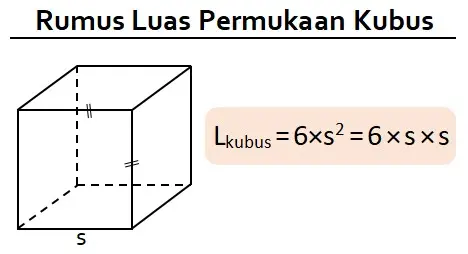
Cara menghitung luas permukaan kubus
Soal:
Sebuah kubus memiliki rusuk 12 cm. Tentukan luas permukaannya!
Jawab:
Dari soal diketahui panjang rusuk s = 12 cm.
Menghitung luas permukaan:
Luas = 6 × s × s
Luas = 6 × 12 × 12 = 864 cm3
Jadi luas permukaan kubus tersebut adalah L kubus = 864 cm3.
Baca Juga: Rumus Volume dan Luas Permukaan Balok
Contoh Soal dan Pembahasan
Beberapa contoh soal dan penyelesaiannya ada di bawah. Selamat Berlatih!
Contoh 1 – Volume bangun di atas adalah ….

Volume bangun di atas adalah ….
A. 294 cm3
B. 343 cm3
C. 444 cm3
D. 468 cm3
Pembahasan:
Diketahui dua buah kubus yang memiliki panjang rusuk berbeda. Panjang rusuk pertama adalah s1 = 5 + 2 = 7 cm dan panjang rusuk kedua adalah s2 = 5 cm.
Menghitung volume kubus pertama (V1):
V1 = s13 = s1 × s1 × s1
V1 = 7 × 7 × 7 = 343 cm3
Menghitung volume kubus kedua (V2):
V1 = s23 = s2 × s2 × s2
V1 = 5 × 5 × 5 = 125 cm3
Jadi, volume bangun tersebut adalah V = V1 + V2 = 343 + 125 = 468 cm3.
Jawaban: D
Contoh 2 – Volume kubus tersebut adalah …
Panjang diagonal sisi kubus 5√2 cm. Volume kubus tersebut adalah ….
A. 100 cm2
B. 150 cm2
C. 200 cm2
D. 300 cm2
Baca Juga: Contoh Soal Volume Bangun Ruang Tingkat SD
Pembahasan:
Untuk mencari volume kubus membutuhkan informasi panjang rusuknya.
- Dari soal diketahui,
- Panjang diagonal sisi: s√2 = 5√2 cm
- Panjang rusuk kubus: s = 5 cm
Menghitung volume:
V = s3 = s × s × s
V = 5 × 5 × 5 = 125 cm2
Jadi, volume kubus tersebut adalah V kubus = 150 cm2.
Jawaban: B
Contoh 3 – Biaya yang diperlukan untuk mengecat seluruh ruangan
Sebuah ruangan berbentuk kubus yang memiliki panjang sisi 11 m. Ruangan tersebut akan dicat dengan biaya pengecatan sebesar Rp20.000,00 per m2. Biaya yang diperlukan untuk mengecat seluruh ruangan tersebut adalah ….
A. Rp968.000,00
B. Rp3.680.000,00
C. Rp6.980.000,00
D. Rp9.680.000,00
Pembahasan:
BIasa yang diperlukan untuk mengecat seluruh ruangan sama dengan luas permunkaan yang akan dicat × biasa. Permukaan yang dicat adalah empat sisi tembok (sisi atas dan bawah tidak dicat).
Luas permukaan dinding yang akan dicat adalah:
L = 4 × (s × s) = 4×(11×11)
L = 4 × 121 = 484 m2
Biaya yang diperlukan untuk mengecat sama dengan luas kubus dikali biasa pengecetan per m2 (Rp20.000,00).
Jumlah biaya yang dibutuhkan
= luas permukaan yang akan dicat × biaya
= 484 × Rp20.000,00 = Rp9.680.000,00
Jadi, biaya yang diperlukan untuk mengecat seluruh ruangan tersebut adalah Rp9.680.000,00.
Jawaban: D
Sekian ulasan mengenai rumus volume kubus dan luas permukaannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Karakteristik Bangun Ruang Sisi Datar