Negasi atau ingkaran dalam bahasan logika matematika memiliki arti lawan atau kebalikan dari pernyataan awal. Nilai kebenaran dari suatu premis dengan ingkaran premis selalu menyatakan hubungan yang berlawanan. Jika suatu premis bernilai benar maka negasi pernyataan majemuk atau premis tersebut bernilai salah. Sebaliknya, jika suatu premis bernilai salah maka negasi pernyataan majemuk atau premis tersebut bernilai benar.
Karakteristik dari pernyataan negasi biasanya ditandai dengan penambahan kata bukan atau tidak. Sebagai contoh diberikan sebuah pernyataan: Saya bisa mengerjakan semua soal dengan baik. Negasi pernyataan majemuk tersebut adalah: Saya tidak bisa mengerjakan semua soal dengan baik.
Negasi pernyataan majemuk memiliki bentuk ekuivalen antara satu ekspresi logika dengan bentuk ekspresi logika lainnya. Misalnya negasi pernyataan majemuk dengan konjungsi ~(p ∧ q) yang ekuivalen dengan ekspresi logika dengan operator disjungsi yaitu ~p ∨ ~q.
Negasi pernyataan majemuk dapat diperoleh dari bentuk ingkaran suatu ekspresi logika yang ekuivalen. Apa saja bentuk ekuivalen ekspresi logika dari negasi pernyataan mejamuk? Bagaimana cara menentukan negasi pernyataan majemuk? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Baca Juga: 4 Macam Operator Logika Matematika [Konjungsi, Disjungsi, Implikasi, dan Biimplikasi]
Negasi Pernyataan Majemuk dengan Konjungsi
Pernyataan majemuk dengan konjungsi ditandai dengan adanya kata penghubung dan, tetapi, seandainya, walaupun, seperti, bahwa, serta supaya. Simbol konjungsi dalam penulisan ekspresi logika mengguana tanda ∧ atau &. Nilai kebenaran dari pernyataan majemuk dengan konjungsi hanya akan bernilai benar (B) jika semua proposisi tunggalnya bernilai benar. Selain itu nilai kebenaran dari pernyataan majemuk dengan konjungsi adalah salah (S).
Sebagai contoh: Jeany adalah siswa yang pintar dan memiliki hobi membaca. Andaikan p = Jeany adalah siswa yang pintar dan q = Jeany memiliki hobi membaca. Penulisan ekspresi logika untuk pernyataan majemuk tersebut adalah p ∧ q atau p & q.
Selanjutnya, bagaimana negasi pernyataan majemuk tersebut pada contoh di atas? Apakah cukup menambahkan kata tidak pada kedua proposisi tunggalnya? Sehingga bentuk negasinya menjadi Jeany adalah bukan siswa yang pintar dan Jeany tidak memiliki hobi membaca (~p ∧ ~q)?
Untuk membuktikannya, perhatikan tabel kebenaran untuk pernyataan majemuk dengan konjungsi dan yang diduga adalah ~p ∧ ~q merupakan bentuk negasinya seperti berikut.
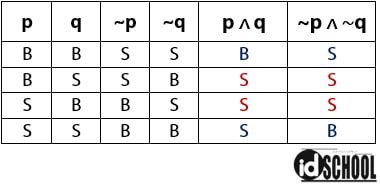
Perhatikan nilai kebenaran untuk kolom p ∧ q dan ~p ∧ ~q! Tidak semua baris pada nilai kebenaran pada kedua kolom tersebut memiliki nilai yang berkebalikan. Kesimpulannya adalah negasi dari p ∧ q bukan ~p ∧ ~q.
Bentuk negasi yang benar untuk p ∧ q adalah ~(p ∧ q) yang ekuibalen dengan ekspresi logika ~p ∨ ~q. Perhatikan tabel kebenaran berikut untuk melihat nilai kebenaran dari kedua ekspresi logika tersebut.
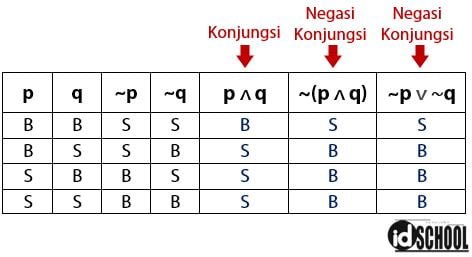
Pada tabel kebenaran di atas, pada kolom p ∧ q memiliki nilai kebenaran yang saling berlawanan dengan kolom ~(p ∧ q) dan ~p ∨ ~q . Artinya, bentuk negasi pernyataan majemuk yang sesuai dengan ekspresi logika p ∧ q adalah ~p ∨ ~q. Sehingga, bentuk negasi untuk contoh konjungsi ini menjadi Jeany adalah bukan siswa yang pintar atau Jeany tidak memiliki hobi membaca.

Baca Juga: Konvers, Invers, dan Kontraposisi dari Suatu Implikasi
Negasi Disjungsi
Pernyataan majemuk dengan disjungsi ditandai dengan penggunaan kata atau sebagai kata penghubungnya. Simbol disjungsi untuk menghubungkan dua proposisi tunggalnya adalah ∨. Nilai kebenaran dari suatu disjungsi hanya akan bernilai salah (S) jika semua proposisi tunggalnya bernilai salah, selain itu nilainya adalah benar (B).
Sebagai contoh sebuah disjungsi: Jeany adalah siswa yang pintar atau memiliki hobi membaca. Misalkan p = Jeany adalah siswa yang pintar, sementara q = Jeany memiliki hobi membaca. Ekspresi logika yang sesuai dengan pernyataan majemuk pada contoh tersebut adalah p ∨ q.
Bentuk negasi disjungsi merupakan pernyataan dengan konjungsi dari ingkaran kedua proposisi tunggalnya. Sehingga, bentuk negasi untuk pernyataan contoh tersebut adalah Jeany adalah bukan siswa yang pintar dan Jeany tidak memiliki hobi membaca.
Kebenaran dari disjungsi dan bentuk negasinya ini dapat dilihat melalui tabel kebenaran berikut.
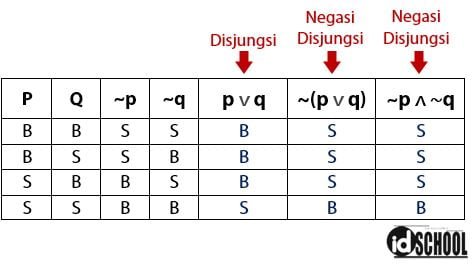
Nilai kebenaran untuk kolom p ∨ q memiliki hubungan yang berlawanan dengan ~(p ∨ q) dan ~p ∧ ~q. Kesimpulannya, bentuk negasi untuk p ∨ q adalah ~(p ∨ q) yang ekuivalen dengan bentuk ~p ∧ ~q.

Baca Juga: Cara Melengkapi Nilai Kebenaran pada Tabel Kebenaran
Negasi Implikasi
Sebuah implikasi ditandai kata penghubung jika … maka … yang disimbolkan garis lurus dengan sebuah anak panah pada ujung kanan (simbol implikasi: →). Nilai kebenaran dari suatu implikasi hanya akan bernilai salah (S) jika anteseden (pendahulu) bernilai benar dan konsekuen (akibat) bernilai Salah (S). Selain kondisi tersebut, nilai kebenara suatu implikasi adalah Benar (B).
Contoh pernyataan dengan implikasi: Jika Jeany adalah siswa yang pintar maka Jeany memiliki hobi membaca. Andaikan p = Jeany adalah siswa yang pintar dan q = Jeany memiliki hobi membaca. Simbol implikasi yang sesuai untuk pernyataan majemuk tersebut adalah p → q.
Tidak sedikit yang mengira bahwa bentuk negasi dari p → q adalah ~p → ~q. Nyatanya, bentuk ~p → ~q merupakan invers dari implikasi p → q. Invers dari suatu implikasi bukan merupakan bentuk negasi dari suatu implikasi.
Negasi suatu implikasi berbentuk konjungsi dari anteseden dan ingkaran konsekuen. Untuk suatu implikasi p → q memiliki bentuk negasi ~(p → q) yang ekuivalen dengan p ∧ ~q. Sehingga, negasi pernyataan majemuk pada contoh tersebut adalah Jeany adalah siswa yang pintar dan Jeany tidak memiliki hobi membaca.
Kebenaran dari implikasi dan bentuk negasinya dapat dilihat melalui tabel kebenaran berikut.
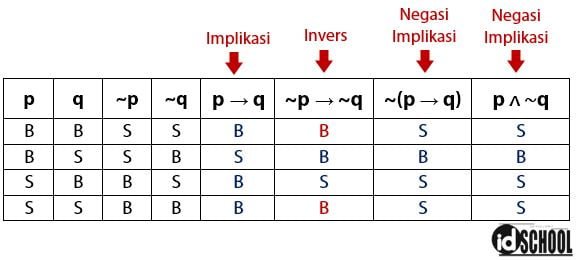
Berdasarkan tabel kebenaran di atas, semua nilai kebenaran untuk kolom p → q berlawanan dengan ~(p → q) dan p ∧ ~q. Kesimpulannya, bentuk negasi untuk p → q adalah ~(p → q) yang ekuivalen dengan bentuk p ∧ ~q.

Baca Juga: Pernyataan Berkuantor Universal dan Eksistensial
Negasi Biimplikasi
Dua proposisi tunggal yang dihubungkan oleh kata penghubung jika dan hanya jika atau bila dan hanya bila merupakan biimplikasi. Simbol biimplikasi adalah garis lurus dengan dua buah anak pada kedua ujungnya (simbol biimplikasi: ↔).
Nilai kebenaran dari suatu biimplikasi akan bernilai benar (B) jika kedua proposisi tunggalnya bernilai sama. Suatu biimplikasi akan bernilai salah (S) jika proposisi tunggalnya memiliki nilai kebenaran yang berbeda.
Contoh biimplikasi: Jeany adalah siswa yang pintar jika dan hanya jika Jeany memiliki hobi membaca. Andaikan p = Jeany adalah siswa yang pintar dan q = Jeany memiliki hobi membaca. Simbol biimplikasi yang sesuai untuk pernyataan majemuk pada contoh adalah p ↔ q.
Bentuk negasi suatu biimplikasi bukan berupa biimplikasi dari ingkaran kedua proposisi tunggalnya [~(p ↔ q) bukan ~p ↔ ~q]. Negasi biimplikasi juga bukan dengan menukar posisi anteseden dan konsekuen [~(p ↔ q) bukan q ↔ p].
Bentuk negasi dari biimplikasi berbentuk disjungsi dari ingkaran sebuah implikasi dan ingkaran konversnya yang memiliki bentuk ekspreso logika: ~(p → q) ∨ ~(p → q). Negasi biimplikasi akan ekuivalen juga dengan bentuk disjungsi dari konjungsi anteseden dan ingkaran konsekuen serta konsekuen dan ingkaran anteseden yang sesuai dengan ekspresi logika: (p ∧ ~q) ∨ (~q ∧ ~p).
Kebenaran dari biimplikasi dan bentuk negasinya dapat dilihat melalui tabel kebenaran berikut.

Baca Juga: 3 Metode Penarikan Kesimpulan pada Logika Matematika
Pada tabel kebenaran di atas, semua nilai kebenaran untuk kolom p ↔ q dan ~(p → q) ∨ ~(p → q) saling berkebalikan. Kesimpulannya, bentuk negasi untuk biimplikasi p ↔ q adalah ~(p ↔ q) yang ekuivalen dengan bentuk ~(p → q) ∨ ~(p → q). Di mana bentuk ~(p → q) ∨ ~(p → q) ekuivalen dengan (p ∧ ~q) ∨ (~q ∧ ~p).
Sehingga, bentuk negasi pernyataan majemuk yang sesuai contoh adalah Jeany adalah siswa yang pintar dan Jenay tidak memiliki hobi membaca atau Jeany memiliki hobi membaca dan Jeany adalah bukan siswa yang pintar.

Demikianlah ulasan materi negasi pernyataan majemuk untuk konjungsi, disjungsi, implikasi, dan biimplikasi. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Tautologi, Kontradiksi, dan Kontingensi
.
