Dua himpunan yang dihubugkan oleh sebuah relasi akan memiliki 3 daerah yaitu daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range). Cara menentukan daerah asal, daerah kawan, dan daerah hasil dilakukan dengan melihat bagaimana hubungan antara dua relasi atau fungsi. Sebuah relasi dan fungsi adalah cara memasangkan anggota dari sebuah himpunan ke anggota himpunan lainnya.
Perlu diketahui bahwa dalam relasi tidak terdapat aturan khusus dalam memasangkan anggota domain dengan anggota kodomain. Pemasangan anggota domain boleh memiliki lebih dari satu hubungan dengan anggota kodomain.
Sebuah relasi yang memiliki aturan khusus untuk memasangkan semua anggota himpunan daerah asal tepat satu ke daerah kawan disebut fungsi atau pemetaan. Inti dari perbedaan relasi dan fungsi/pemetaan terdapat bagaimana daerah asal atau domain dipasangkan.
Himpunan sendiri merupakan sekumpulan obyek-obyek dengan definisi/keterangan yang jelas. Contoh himpunan adalah warna-warna pelangi, di mana himpunan tersebut membuat obyek warna merah, jingga, kuning, hijau, biru, nila, dan ungu. Contoh lainnya adalah himpunan bilangan asli kurang dari 9 yaitu A = {1, 2, 3, 4, 5, 6, 7, 8}.

Jika terdapat dua buah himpunan yang dihubungkan oleh sebuah relasi maka akan terdapat daerah asal, kawan, dan range.
Bagaimana cara menentukan daerah asal atau domain, yang mana daerah kawan atau kodomain, dan yang mana daerah hasil atau range? Sobat idschool dapat mencari tahu jawabannya melalui ulasan cara menentukan daerah awal, kawan, dan hasil di bawah.
Table of Contents
- Contoh Relasi Antara Dua Himpunan
- Cara Menentukan Daerah Asal (Domain)
- Daerah Kawan ~ Kodomain
- Cara Menentukan Daerah Hasil (Range)
- Contoh Soal dan Pembahasan Cara Menentukan Daerah Asal, Kawan, dan Hasil
Baca Juga: Cara Menentukan Banyaknya Anggota Himpunan Bagian
Contoh Relasi Antara Dua Himpunan
Fokus bahasan pada halaman ini adalah mengetahui mana yang disebut daerah asal, daerah kawan, dan daerah hasil. Untuk menjelaskan bagian himpunan yang termasuk himpunan daerah asal, daerah kawan, atau daerah hasil.
Deibrikan sebuah relasi yang menyatakan hubungan “ibu kota negara dari”. Diketahui bahwa himpunan A memuat nama-nama ibu kota negara yang terdiri dari Tokyo, New Delhi, Washington, D.C, Jakarta, dan Kuala Lumpur. Sementara himpunan B memuat nama-nama negara yang terdiri dari Indonesia, Malaysia, Jepang, Singapura, dan India.
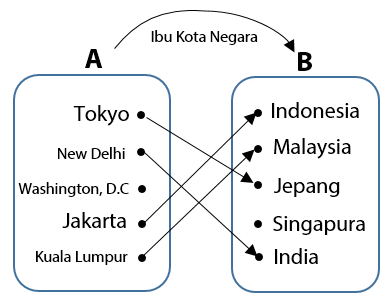
Diagram panah di atas menyatakan relasi antara himpunan A dan himpunan B. Sebuah relasi ibu kota negara dari memasangkan anggota-anggota himpunan A dengan anggota-anggota himpunan B.
Relasi dari himpunan A ke himpunan B yang menyatakan hubungan ibu kota negara dari. Daerah asal dari relasi tersebut meliputi Tokyo, New Delhi, Washington D.C, Jakarta, dan Kuala Lumpur. Daerah kawan untuk relasi tersebut adalah Indonesia, Malaysia, Jepang, Singapura, dan India. Sementara, daerah hasil untuk relasi tersebut adalah Indonesia, Malaysia, Jepang, dan India.
Daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range) dari relasi ibu kota negara dari himpunan A ke himpunan B secara ringkas dapat dituliskan seperti berikut.
Domain: {Tokyo, New Delhi, Washington D.C, Jakarta, Kuala Lumpur}
Kodomain: {Indonesia, Malaysia, Jepang, Singapura, India}
Range: {Indonesia, Malaysia, Jepang, India}
Baca Juga: Himpunan dan Diagram Venn
Penjelasan bagaimana cara menentukan daerah asal, daerah kawan, dan daerah hasil seperti di atas dapat dipelajari melalui setiap ulasan berikut.
Cara Menentukan Daerah Asal (Domain)
Daerah asal disebut juga sebagai domain. Pengertian dari domain adalah himpunan tidak kosong dimana sebuah relasi didefinisikan. Perhatikan kembali relasi ibu kota negara dari yang diberikan seperti diagram panah di atas.
Diagram panah tersebut mendefinisikan himpunan A yang memuat nama-nama ibu kota negara yang terdiri atas Tokyo, New Delhi, Washington, D.C, Jakarta, dan Kuala Lumpur. Sehingga, domain atau daerah asal dari relasi ibu kota negara adalah Tokyo, New Delhi, Washington, D.C, Jakarta, dan Kuala Lumpur.
Sehingga dapat disimpulkan bahwa cara menentukan daerah asal adalah mengamati byek-obyek pada himpunan yang akan dipasangkan.
Daerah Kawan ~ Kodomain
Sebutan lain untuk daerah kawan adalah kodomain. Pengertian dari kodomain adalah himpunan tidak kosong dimana anggota domain memiliki pasangan sesuai relasi yang didefinisikan.
Dalam relasi ibu kota negara yang diberikan sebelumnya, didefinisikan himpunan B yang memiliki anggota nama – nama negara yang terdiri atas Indonesia, Malaysia, Jepang, Singapura, dan India. Semua anggota himpunan B tersebut merupakan daerah kawan atau kodomain
Jadi, kodomain atau daerah kawan dari relasi ibu kota negara tersebut adalah Indonesia, Malaysia, Jepang, Singapura, dan India.
Cara Menentukan Daerah Hasil (Range)
Berikutnya adalah daerah hasil yang biasa disebut sebagai range. Daerah hasil atau range adalah sebuah himpunan bagian dari daerah kawan (kodomain) yang anggotanya merupakan pasangan anggota domain yang memenuhi relasi yang didefinisikan. Ringkasnya, Range merupakan anggota himpunan kawan (kodomain) yang memiliki pasangan pada himpunan daerah asal (domain).
Dari contoh relasi ibu kota negara, himpunan B yang terpasangkan dengan himpunan A adalah Indonesia, Malaysia, Jepang, dan India. Sedangkan Singapura pada himpunan B tidak terpasangkan atau tidak memiliki pasangan dengan anggota pada himpunan A.
Jadi, daerah hasil atau range untuk relasi ibu kota negara seperti yang diberikan di atas adalah Indonesia, Malaysia, Jepang, dan India.
Baca Juga: Contoh-Contoh Kalimat Terbuka dan Terutup dalam Matematika
Contoh Soal dan Pembahasan Cara Menentukan Daerah Asal, Kawan, dan Hasil
Sobat idschool dapat meningkatkan pemahaman materi bagaimana cara menentukan daerah asal, kawan, dan hasil melalui contoh soal di bawah. Setiap contoh soal yang diberikan dilengkapi pembahasan bagaimana cara menentukan daerah asal, kawan, dan hasil. Pembahasan tersebut dapat sobat idschool gunakan sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal Cara Menentukan Daerah Asal, Kawan, dan Hasil
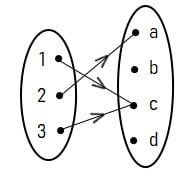
Daerah asal yang sesuai untuk diagram panah di atas adalah ….
A. {1, 2, 3}
B. {a, c}
C. {b, d}
D. {a, b, c, d}
Pembahasan:
Himpunan daerah asal memuat semua obyek-obyek yang akan dipasangkan. Dari diagram panah yang diberikan, semua obyek yang akan dipasangkan adalah 1, 2, dan 3. Sementera obyek yang akan menjadi pasangan adalah a, b, c, dan d, serta obyek yang terpasangkan adalah a dan c.
Sehingga dapat diperoleh kesimpulan bahwa:
Domain (aerah asal): {1, 2, 3}
Kodomain (daerah kawan): {a, b, c, d}
Range (daerah hasil): {a, c}
Jadi, daerah asal yang sesuai untuk diagram panah di atas adalah {1, 2, 3}.
Jawaban: A
Contoh 2 – Soal Cara Menentukan Daerah Asal, Kawan, dan Hasil
Diagram panah berikut menunjukkan relasi dari himpunan A ke B

Daerah hasil dari relasi tersebut adalah . . . .
A. {1, 2, 3, 4}
B. {1, 4, 9, 16}
C. {1, 4, 9, 12, 16}
D. {1, 2, 3, 4, 9, 12, 16}
Pembahasan:
Daerah hasil atau range merupakan anggota himpunan kawan (kodomain) yang memiliki pasangan pada himpunan daerah asal (domain). Jadi, daerah hasil atau range untuk relasi A ke B pada soal adalah {1, 4, 9, 16}.
Jawaban: B
Baca Juga: Contoh Persamaan Matematika yang Merupakan Fungsi
Contoh 3 – Soal Cara Menentukan Daerah Asal, Kawan, dan Hasil
Diagram panah berikut menunjukkan relasi dari himpunan A ke himpunan B.

Daerah hasil dari relasi tersebut adalah . . . .
A. {0, 1, 4, 9}
B. {2, 3, 5, 6, 7, 8}
C. { –2, –1, 0, 1, 2, 3}
d. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Pembahasan:
Anggota himpunan daerah kawan (kodomain) yang memiliki pasangan pada daerah asal (domain) adalah 0, 1, 4, dan 9. Jadi daerah hasil dari relasi pada soal yang diberikan adalah {0, 1, 4, 9}.
Jawban: A
Demikianlah tadi ulasan bagaimana cara menentukan daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range). Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Kumpulan Contoh Soal Relasi dan Fungsi Level Aplikasi (sesuai kisi – kisi UN)
