Jarak garis ke bidang sama dengan panjang ruas garis terpendek yang menghubungkan sebuah titik pada garis dan sebuah titik pada bidang. Ruas garis tersebut adalah sebuah garis yang tegak lurus dengan garis dan bidang. Jadi, jarak garis ke bidang adalah panjang segmen garis terpendek yang tegak lurus dengan suatu garis dan bidang.
Rumus yang dapat digunakan untuk menghitung jarak garis ke bidang meliputi Teorema Pythagoras, Aturan Cosinus, fungsi trigonometri, luas segitiga, atau rumus-rumus lain yang berkaitan. Penggunaan rumus disesuaikan dengan informasi apa yang dimiliki.
Cara menghitung jarak garis ke bidang dapat memiliki lebih dari satu cara penyelesaian. Namun pemilihan langkah penyelesaian yang tepat dapat mempermudah cara menentukan jarak garis ke bidang.
Bagaimana cara menghitung jarak garis ke bidang? Sobat idshcool dapat mencari tahu jawabannya melalui ulasan di bawah.
Daftar isi:
Baca Juga: Pasangan Garis Saling Sejajar, Berpotongan, dan Tegak Lurus pada Kubus
Menentukan Jarak Garis ke Bidang
Cara menentukan suatu ruas garis yang menjadi jarak garis ke bidang dapat menggunakan bantuan bidang yang tegak lurus dengan garis dan bidang tersebut. Perpotongan bidang dengan bidang yang tegak lurus tersebut berupa sebuah garis.
Jarak garis hasil perpotongan bidang dan bidang dengan sebuah garis merupakan ruas garis yang menjadi jarak garis ke bidang.

Secara ringkas, cara menentukan segmen garis yang menjadi jarak garis ke bidang meliputi langkah-langkah penyelesaian berikut.
- Buat bidang yang tegak lurus dengan garis dan bidang
- Perpotongan bidang dengan bidang menghasilkan sebuah garis
- Jarak garis yang dihasilkan pada bidang dengan garis di luar bidang merupakan jarak garis ke bidang
Baca Juga: Kumpulan Rumus dan Materi Dimensi Tiga
Cara Menghitung Jarak Garis ke Bidang
Setelah bisa menentukan segmen garis yang menjadi jarak garis ke bidang, berikutnya adalah menentukan panjang segmen garis tersebut.
Untuk menghitung jarak garis ke bidang perlu menentukan panjang segmen garis yang. Bagaimana cara menentukan jarak garis ke bidang terdapat pada langkah penyelesaian soal berikut.
Soal: Jarak garis AD ke bidang BCHE pada kubus ABCD.EFGH yang memiliki panjang rusuk 12 cm adalah ….
Penyelesaian:
Bidang yang tegak lurus dengan garis AD dan bidang BCHE pada kubus ABCD,EFGH adalah bidang ADGF. Perpotongan bidang BCHE dan ADGF adalah garis PQ.

Jarak garis AD ke bidang BCHE sama dengan jarak garis AD ke garis PQ yaitu AP = DQ. Di mana panjang AP = PQ = setengah garis diagonal bidang kubus.
Panjang diagonal bidang suatu kubus dengan panjang rusuk a adalah a√2. Untuk kubus dengan panjang rusuk = 12 cm memiliki panjang diagonal bidang = 12√2 cm. Sehingga, panjang AP = PQ = ½ × 12√2 = 6√2 cm.
Jadi, jarak garis AD ke bidang BCHE pada kubus ABCD.EFGH yang memiliki panjang rusuk 12 cm adalah AP = 6√2 cm.
Baca Juga: Rumus Besar Sudut Antara Garis dan Bidang
Contoh soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idshool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat berlatih!
Contoh 1 – Soal jarak garis ke bidang
Diketahui kubus ABCD.EFGH dengan panjang rusuk 8 cm. Jarak garis HF ke bidang BDG adalah ….
A. 8/3√3 cm
B. 4/3√3 cm
C. 8√3 cm
D. 4√3 cm
E. √3 cm
Pembahasan:
Bidang yang tegak lurus dengan garis HF dan bidang BDG adalah ACGE. Perpotongan bidang ACGE dengan bidang BDG adalah garis GP. Sehingga, jarak garis HF ke bidang BDG sama dengan jarak garis HF ke garis GP yaitu garis QR.
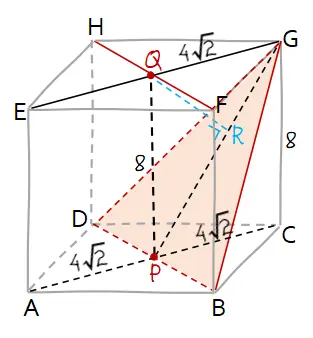
Titik P dan titik Q adalah perpotongan diagonal kubus, sehingga panjang ruas garis PC = QG = 4√2 cm. Sementara panjang garis PQ = CG = rusuk kubus = 8 cm.
Untuk menghitung panjang garis QR, perhatikan segitiga PQG. Segitiga tersebut dapat dipandang dengan dua cara. Pertama untuk segitiga dengan alas PG dan tinggi QR. Kedua untuk segitiga dengan alas QG dan tinggi QP.
Diketahui:
PC = QG = 4√2 cm
PQ = CG = 8 cm
Panjang PG dapat dihitung menggunakan Teorema Pythagoras dari segitiga siku-siku PCG. Cara menghitung panjang ruas garis PG terdapat pada langkah penyelesaian berikut.
1) Menghitung panjang PG:
PG2 = QG2 + PQ2 = (4√2)2 + 82
PG2 = 32 + 64 = 96
PG = √(16×6) = √16 × √6 = 4√6 cm
Selanjutnya, panjang ruas garis QR dapat dihitung menggunakan luas segitiga seperti perhitungan berikut.
2) Menghitung tinggi QR:
Luas ΔPQG = Luas ΔPQG 1/2 × PG × QR = 1/2 × QG × PQ 4√6 × QR = 4√2 × 8
QR = 8√2/√6
3) Menyederhanakan nilai QR:
QR = 8√2/√6 × √6/√6
QR = 8√12/6 = 8/6√12
QR = 4/3√(4×3) = 4/3 × √4 × √3
QR = 4/3 × 2 × √3 = 8/3√3 cm
Jadi, jarak garis HF ke bidang BDG adalah QR = 8/3√3 cm.
Jawaban: A
Contoh 2 – Soal jarak garis ke bidang
Diketahui panjang rusuk kubus ABCD EFGH adalah 6 cm. Titik K, titik L, titik M, dan titik N berturut-turut merupakan titik tengah dari rusuk AB, BC, EH, dan GH. Jarak garis KL ke bidang DMN adalah ….
A. 10 cm
B. 8 cm
C. 6 cm
D. 4 cm
E. 3 cm
Pembahasan:
Bidang yang tegak lurus dengan garis KL dan bidang DMN adalah bidang BDHF. Perpotongan bidang BDHF dengan bidang DMN adalah garis DP.
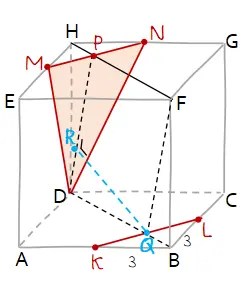
Jarak garis KL ke bidang DMN sama dengan jarak garis KL ke garis DP yaitu ruas garis QR.
Panjang garis QR dapat dihitung menggunakan rumus luas jajar genjang DBFP.
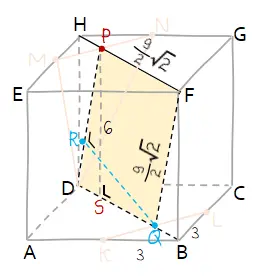
Dari segitiga sama kaki KBL dapat ditentukan panjang garis KL menggunakan Teorema Pythagoras. Di mana panjang garis KL = 3√2 cm.
1) Menghitung panjang BQ:
Luas ΔKBL = Luas ΔKBL
1/2×KL×BQ = 1/2×KB×BL 3√2 × BQ = 3 × 3
BQ = 3/√2 = 3/2√2 cm
Panjang garis diagonal bidang pada kubus sama dengan rusuk√2. Diketahui panjang rusuk kubus ABCD.EFGH adalah 6 cm. Sehingga, panjang diagonal kubus BD = 6√2 cm.
2) Menghitung panjang DQ:
DQ + BQ = BD
DQ + 3/2√2 = 6√2
DQ = 6√2 − 3/2√2
DQ = 12/2√2 − 3/2√2 = 9/2√2 cm
Dengan cara yang sama untuk menghitung panjang garis DQ dapat diperoleh panjang garis FP = DQ = 9/2√2 cm.
3) Menghitung panjang garis FQ: perhatikan segitiga siku-siku FBQ
FQ2 = FB2 + BQ2 = 62 + (3/2√2)2
FQ2 = 36 + 18/4 = 144/4 + 18/4 = 162/4
FQ = √(162/4) = √(81×2)/√4
FQ = √81 × √2/2 = 9√2/2 = 9/2√2 cm
Panjang garis DP dapat dihitung dengan cara yang sama untuk mencari panjang garis FQ. Begitu juga untuk hasilnya akan diperoleh nilai yang sama yaitu DP = FQ = 9/2√2.
4) Menghitung panjang QR:
Luas DQFH = Luas DQFH
DP × QR = DQ × PS 9/2√2 × QR = 9/2√2 × 6
QR = 6 cm
Jadi jarak garis PQ ke bidang DRS adalah QR = 6 cm.
Jawaban: C
Demikianlah ulasan jarak garis ke bidang pada bahasan materi dimensi tiga. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Jarak Bidang Ke Bidang
