Pertidaksamaan nilai mutlak bentuk pecahan ditandai dari fungsi nilai mutlak dengan pecahan dan tanda pertidaksamaan. Contoh sederhana pertidaksamaan nilai mutlak bentuk pecahan adalah |2x + 1/3| < 5. Himpunan penyelesaian dari pertidaksamaan nilai mutlak adalah semua nilai x yang memenuhi pertidaksamaan tersebut.
Nilai mutlak merupakan sebuah fungsi yang selalu membuat nilai di dalamnya fungsi bernilai positif. Simbol fungsi nilai mutlak ditandai dengan dua buah garis lurus yang mengapit suatu fungsi. Misalkan fungsi nilai mutlak untuk x dinyatakan dalam bentuk fungsi | x |. Fungsi nilai mutlak untuk x – 3 adalah |x – 3|. Fungsi nilai mutlak dapat meliputi bentuk persamaan dan pertidaksamaan.
Fungsi persamaan nilai mutlak ditandai dengan operator hubung sama dengan (=) antar ruas. Contoh persamaan nilai mutlak adalah | x | = – 3, | x – 3 | = 5, dan lain sebagainya.
Sdangkan pertidaksamaan nilai mutlak dihubungkan oleh tanda pertidaksamaan seperti lebih dari (>), kurang dari (<), lebih dari atau sama dengan (≥), dan kurang dari atau sama dengan (≤). Contoh pertidaksamaan nilai mutlak adalah | x | < – 3, | x – 3 | ≤ 5, dan lain sebagainya.

Setiap fungsi persamaan atau pertidaksamaan nilai mutlak memiliki solusi nilai variabel yang memenuhi persamaan atau pertidaksamaan. Pada fungsi persamaan nilai mutlak, solusinya berupa suatu nilai yang memenuhi persamaan. Sedangkan pada pertidaksamaan nilai mutlak, solusi nilai biasanya berupa suatu himpunan penyelesaian.
Beberapa bentuk soal fungsi pertidaksamaan nilai mutlak diberikan dalam bentuk yang bervariasi, misalnya bentuk pecahan. Bagaimana cara menyelesaikan pertidaksamaan nilai mutlak dalam bentuk pecahan? Sobat idschool dapat mencari tahu caranya melalui ulasan di bawah.
Table of Contents
- Pengertian Nilai mutlak
- Sifat-Sifat Pertidaksamaan Nilai Mutlak
- Cara Mengerjakan Pertidaksamaan Nilai Mutlak Bentuk Pecahan
- Contoh Soal dan Pembahasan
Baca Juga: Persamaan dan Pertidaksamaan Linear Satu Variabel
Pengertian Nilai mutlak
Definisi nilai mutlak digambarkan sebagai jarak titik nol ke suatu titik pada sebuah garis bilangan. Misalnya pada titik x = 3, jarak titik nol ke titik tersebut adalah tiga satuan. Jadi, nilai mutlak dari x = 3 atau | 3 | = 3. Contoh lain, misalnya pada titik x = –3, jarak titik nol ke titik tersebut juga sama dengan 3. Jadi, nilai mutlak dari x atau | –3 | = 3.
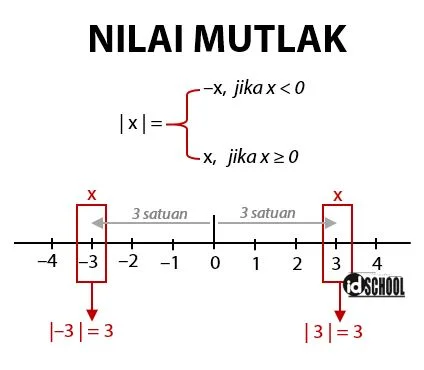
Sifat-Sifat Pertidaksamaan Nilai Mutlak
Cara mengerjakan pertidaksamaan nilai mutlak memerlukan sifat-sifat nilai mutlak agar lebih mudah untuk diselesaikan. Ada beberapa sifat-sifat pertidaksamaan nilai mutlak yang perlu sobat idschool ketahui. Daftar sifat-sifat pertidaksamaan nilai mutlak diberikan seperti berikut.

Selain beberapa sifat pertidaksamaan nilai mutlak di atas, masih terdapat beberapa sifat pertidaksamaan nilai mutlak lainnya. Namun, beberapa sifat pertidaksamaan nilai mutlak di atas merupakan sifat-sifat yang paling sering digunakan. Contoh penggunaan sifat-sifat pertidaksamaan nilai mutlak ditunjukkan untuk menyelesaikan contoh soal di bawah.
Soal:
Tentukan himpunan penyelesaian yang memenuhi | x – 3 | < 5!
Penyelesaian:
Berdasarkan sifat pertidaksamaan nilai mutlak, bentuk pertidaksamaan tersebut dapat diubah dalam sebuah persamaan yang tidak memumat simbol nilai mutlak. Perhatikan sifat pertidaksamaan nomor 1 pada daftar sifat-sifat pertidaksamaan nilai mutlak di atas. Contoh penggunaan sifat-sifat tersebut digunakan seperti pada penyelesaian soal di bawah.
| x – 3 | < 5
–5 < x – 3 < 5
–5 + 3 < x < 5 + 3
2 < x < 8
Jadi, himpunan penyelesaian untuk pertidaksamaan nilai mutlak | x – 3 | < 5 adalah 2 < x < 8.
Baca Juga: Cara Menentukan Persamaan Grafik Fungsi Kuadrat Dari Gambar Kurva
Cara Mengerjakan Pertidaksamaan Nilai Mutlak Bentuk Pecahan
Salah satu bentuk variasi soal pertidakamaan nilai mutlak adalah nilai mutlak dengan fungsi pecahan. Proses pengerjaan soal pertidaksamaan nilai mutlak bentuk pecahan tidak jauh berbeda dengan pertidaksamaan nilai mutlak bentuk lainnya. Langkah pertama yaitu merubah bentuk pertidaksamaan nilai mutlak kedalam bentuk pertidaksamaan biasa sesuai pada sifat-sifat pertidaksamaan nilai mutlak.
Setelah mendapat bentuk pertidaksamaan biasa, langkah beriktunya adalah menyelesaikan pertidaksamaan tersebut. Berikutnya, langkah yang perlu diselesaikan adalah menyimpulkan himpunan penyelesaian yang memenuhi.
Secara ringkas, cara mengerjakan pertidaksamaan nilai mutlak bentuk pecahan sesuai dengan langkah-langkah berikut.
- Merubah pertidaksamaan nilai mutlak ke dalam pertidaksamaan biasa sesuai sifat-sifat pertidaksamaan nilai mutlak
- Menyelesaikan bentuk pertidaksamaan
- Menentukan himpunan penyelesaian
Sebagai contoh, perhatikan soal dan cara menyelesaikan pertidaksamaan nilai mutlak bentuk pecahan berikut.

Berdasarkan langkah ketiga dapat diperoleh himpunan yang memenuhi persamaan yaitu –2 ≤ x ≤ 2/3.
Baca Juga: Sistem Persamaan Linear Tiga Variabel (SPLTV)
Contoh Soal dan Pembahasan
Beberapa contoh soal berikut dapat menambah pemahaman cara menyelesaikan pertidaksamaan nilai mutlak bentuk pecahan. Setiap contoh soal dilengkapi dengan pembahasan. Sobat idschool dapat menjadikan pembahasan tersebut sebagai tolak ukur keberhasilan dalam mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Pertidaksamaan Nilai Mutlak Bentuk Pecahan
Himpunan penyelesaian yang memenuhi pertidaksamaan nilai mutlak | ½x + 6 | ≥ 9 adalah ….
A. –30 < x < 6
B. –30 ≤ x ≤ 6
C. x ≤ –6 atau x ≥ 30
D. x ≤ –30 atau x ≥ 6
E. x < –30 atau x > 6
Pembahasan:
Berdasarkan sifat pertidaksamaan nilai mutlak, pertidaksamaan nilai mutlak | ½x + 6 | ≥ 9 ekuivalen dengan bentuk pertidaksamaan ½x + 6 ≤ –9 atau ½x + 6 ≥ 9.
Himpunan penyelesaian untuk ½x + 6 ≤ –9:
½x + 6 ≤ –9
½x ≤ –9 – 6
½x ≤ –15
x ≤ 2 (–15)
x ≤ –30
Himpunan penyelesaian untuk ½x + 6 ≥ 9:
½x + 6 ≥ 9
½x ≥ 9 – 6
½x ≥ 3
x ≥ 2 (3)
x ≥ 6
Jadi, himpunan penyelesaian yang memenuhi pertidaksamaan nilai mutlak | ½x + 6 | ≥ 9 adalah x ≤ –30 atau x ≥ 6.
Jawaban: D
Contoh 2 – Soal Pertidaksamaan Nilai Mutlak Bentuk Pecahan

Pembahasan:
Pertidaksamaan yang sesuai untuk fungsi nilai mutlak berdasarkan sifat pertidaksamaan nilai mutlak pada soal adalah sebagai berikut.
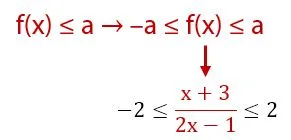
Pertidaksamaan seperti yang diberikan di atas terdiri dari dua buah pertidaksamaan. Pertama adalah pertidaksamaan f(x) ≥ –2. Kedua adalah pertidaksamaan f(x) ≤ 2. Himpunan penyelesaian yang memenuhi f(x) adalah gabungan dua himpunan dari dua pertidaksamaan tersebut.
Mencari himpunan penyelesaian untuk pertidaksamaan pertama f(x) ≥ –2.
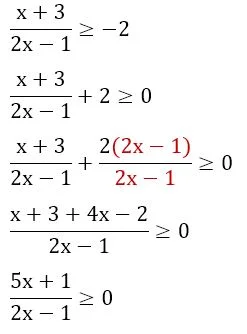
Pembuat nol untuk pembilang adalah x = –1/5 dan pembuat nol untuk penyebut adalah x = ½. Himpunan penyelesaian yang memenuhi pertidaksamaan pertama adalah sebagai berikut.

Mencari himpunan penyelesaian untuk pertidaksamaan pertama f(x) ≤ 2.

Pembuat nol untuk pembilang adalah x = 5/3 dan pembuat nol untuk penyebut adalah x = ½. Himpunan penyelesaian yang memenuhi pertidaksamaan pertama adalah sebagai berikut.
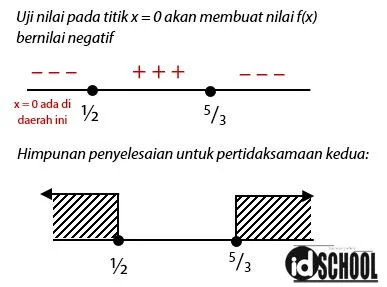
Selanjutnya adalah mencari gabungan himpunan penyelesaian pada pertidaksamaan pertama dan kedua.
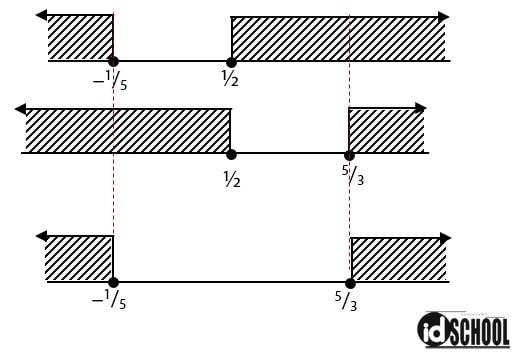
Jadi, himpunan penyelesain yang memenuhi pertidaksamaan nilai mutlak bentuk pecahan tersebut adalah {x | x ≤ –1/5 atau x ≥ 5/3, x ∈ R }.
Jawaban: C
Demikianlah tadi ulasan cara menyelesaikan pertidaksamaan nilai mutlak bentuk pecahan. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Himpunan Penyelesaian Pertidaksamaan Kuadrat
