Masalah seputar program linear memiliki kedekatan dengan permasalahan sehari-hari. Sehingga, bentuk soal pada bahasan materi program linear banyak diberikan dalam soal cerita. Bentuk soal cerita program linear dapat dibuat menjadi sistem persamaan linear. Di mana persamaan linear adalah persamaan matematika yang memiliki variabel dengan pangkat tertinggi sama dengan satu. Sistem persamaan linear berarti terdapat beberapa persamaan linear yang saling berkaitan. Solusi dari sistem persamaan linear tersebut merupakan solusi dari soal cerita program linear.
Contoh permasalahan program linear adalah bagaimana cara memaksimalkan keuntungan atau meminimumkan biaya produksi. Dua bentuk soal berikut merupakan contoh soal cerita program linear dengan fungsi tujuan memaksimalkan dan meminimumkan.
Baca Juga: Cara Menggambar Persamaan Linear
Bagaimana cara melakukan pemodelan soal cerita program linear ke persamaan matematika? Ada beberapa langkah yang perlu dikerjakan dalam menyelesaikan soal cerita program linear? Apa saja langkah kerja untuk menyelesaikan soal cerita program linear? Bagaimana cara menyelesaikan soal certia program linear? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
- Pemodelan Matematika
- Langkah-Langkah Menyelesaikan Soal Cerita Program Linear
- Contoh Soal dan Pembahasan
Pemodelan Matematika
Pemodelan matematika adalah cara untuk membentuk soal cerita ke dalam persamaan-persamaan matematika. Setiap persamaan matemtika yang dibentuk disesuaikan dengan informasi yang diberikan dengan mengganti obyek pembicaraan dengan suatu variabel. Bentuk persamaan-persamaan tersebut nantinya diselesaikan yang kemudian menjadi solusi dari soal cerita program linear.
Contoh cara memodelkan masalah dari soal cerita ke persamaan matematika dapat dilihat seperti pada penyelesaian soal di bawah.
Soal:
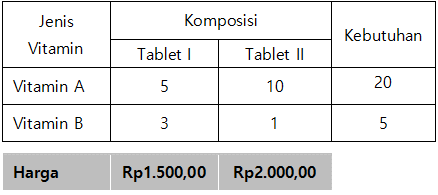
Seorang atlet diwajibkan makan dua jenis tablet setiap hari. Tablet pertama mengandung 5 unit vitamin A dan 3 unit vitamin B, sedangkan tablet kedua mengandung 10 unit vitamin A dan 1 unit vitamin B. Dalam satu hari, atlet itu memerlukan 20 unit vitamin A dan 5 unit vitamin B. Harga tiap-tiap tablet, Rp 1.500 dan Rp2.000.
Modelkan masalah tersebut ke dalam bentuk model matematika!
Penyelesaian:
Berdasarkan keterangan yang diberikan pada soal dapat disimpulkan beberapa informasi seperti berikut.
Komposisi tablet 1:
vitamin A = 5 unit
vitamin B = 3 unit
Komposisi tablet 2:
vitamin A = 10 unit
vitamin B = 1 unit
Kebutuhan atlet:
vitamin A = 20 unit
vitamin B = 5 unit
Diketahui juga bahwa harga untuk tablet I adalah Rp1.500,00 dan harga untuk tabel II adalah Rp2.000,00. Untuk memudahkan pemodelan, buatlah sebuah tabel seperti yang ditunjukkan pada cara berikut.
Misalkan variable x untuk tablet I yang dibutuhkan atlet dan y untuk banyak tablet II yang dibutuhkan atlet. Persamaan yang sesuai untuk keterangan dapat dibentuk seperti berikut.
5x + 10y ≥ 20 → x + 2y ≥ 4
3x + y ≥ 5
x ≥ 0
y ≥ 0
Fungsi tujuan meminimumkan: Z 1.500x + 2.000y
Baca Juga: Perhitungan Keuntungan Maksimum dari Biaya Parkir
Langkah-Langkah Menyelesaikan Soal Cerita Program Linear
Pemodelan matematika seperti yang diberikan pada contoh di atas adalah langkah pertama. Setelah mendapatkan pemodelan seperti pada sistem persamaan linear di atas, selanjutnya adalah menentukan fungsi tujuan yang sesuai. Cara menyelesaiakannya dapat menggunakan beberapa metode seperti garis selidik dan uji titik pojok. Cara yang lebih sering digunakan adalah metode uji titik pojok.
Secara ringkas, ada tiga langkah yang digunakan untuk menyelesaian soal cerita program linear. Ketiga langkah tersebut antara lain meliputi memodelkan soal cerita, menentukan himpunan penyelesaian, dan menghitung nilai fungsi tujuan (fungsi obyektif) yang sesuai.
Memodelkan soal cerita dilakukan dengan menggunakan pemisalan variabel untuk obyek-obyek yang sedangkan dibicarakan. Hasil dari pemodelan dari soal cerita berupa beberapa persamaan linear yang disebut sistem persamaan linear.
Dari sistem persamaan linear yang diperoleh kemudian dapat ditentukan himpunan penyelesaian berupa luas daerah yang dibatas oleh garis-garis lurus. Garis-garis lurus tersebut merupakan garis yang mewakili persamaan linear.
Dalam himpunan penyelesaian memuat nilai maksimal, nilai minimal, dan nilai lain untuk fungsi tujuan/obyektif. Nilai maksimal adalah nilai tertinggi dari fungsi obyektif, sedangkan nilai minimal adalah nilai terendah dari fungsi obyektif.
Baca Juga: Cara Menyelesaian Sistem Persamaan Linear Dua Variabel
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Cerita Program Linear
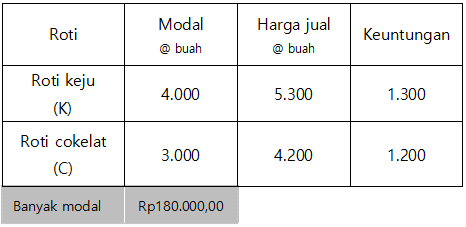
Seorang pedagang roti keju dan roti cokelat dapat menjual tidak lebih dari 50 porsi setiap harinya. Besar modal yang dibutuhkan untuk membuat sebuah roti keju adalah Rp4.000,00. Sedangkan modal untuk membuat sebuah roti cokelat adalah Rp3.000,00. Jumlah modal yang dimiliki pedagangan tersebut adalah RP180.000,00. Jika roti keju dijual Rp5.300,00/buah dan roti cokelat dijual Rp4.200,00/buah maka keuntungan maksimum yang diperoleh pedagang tersebut adalah ….
A. Rp58.000,00
B. Rp62.000,00
C. Rp63.000,00
D. Rp64.000,00
E. Rp72.000,00
Pembahasan:
Langkah pertama adalah membut tabel yang dibutuhkan untuk memodelkan sesuai soal cerita program linear pada soal di atas.
Misalkan banyak roti keju yang terjual agar keuntungan maksimu adalah K dan banyak roti cokelat yang terjual adalah C. Maka pemodelan yang sesuai dengan pernyataan-pernyataan pada soal dapat diperoleh seperti cara berikut.
Persamaan i):
dari kolom modal dapat diperoleh persamaan 4.000K + 3.000C ≤ 180.000 → 4K + 3C ≤ 180
Persamaan ii):
diketahui bahwa jumlah roti keju dan roti cokelat dapat menjual tidak lebih dari 50 porsi, sehingga dapat diperoleh persamaan K + C ≤ 50
Persamaan iii):
dari kolom keuntukan dapat diperoleh fungsi obyektif: Z = 1.300K + 1.200C
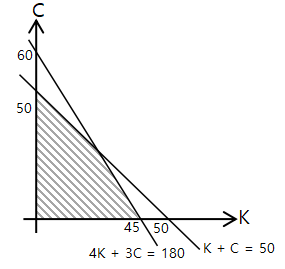
Dari persamaan i) dan persamaan ii) dapat diperoleh daerah yang memuat himpunan penyelesaian seperti berikut.
Dari gambar di atas dapat diperoleh 4 titik sudut yaitu O (0, 0), P(0, 50), R (45, 0), dan titik Q yang belum diketahui letak koordinatnya. Koordinat letak titik Q dapat dicari melalui metode substitusi-elimisai pada SPLDV seperti yang ditunjukkan pada cara berikut.
Eliminasi C untuk mendapatkan nilai K dari persamaan i) dan persamaan ii):
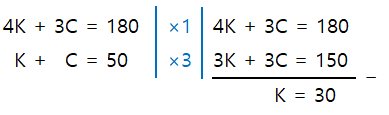
Menghitung nilai C:
C + K = 50
C + 30 = 50
C = 50 ‒ 30 = 20
Sehingga diperoleh koordinat titik Q adalah (30, 20)
Selanjutnya, substitusi setiap titik O, P, Q, dan R ke persamaan fungsi obyektif pada persamaan iii) Z = 1.300K + 1.200C untuk mengetahui kuntungan maksimum yang dapat diperoleh.
O(0, 0) → Z = 1.300×0 + 1.200×0 = 0
P(0, 50) → Z = 1.300×0 + 1.200×50 = 60.000
Q(30, 20)→ Z = 1.300×30 + 1.200×20 = 63.000
R(45, 0)→ Z = 1.300×45 + 1.200×0 = 58.500
Jadi, keuntungan maksimum yang diperoleh pedagang tersebut adalah Rp63.000,00.
Jawaban: C
Contoh 2 – Soal Cerita Program Linear
Untuk membuat 1 liter minuman jenis A diperlukan 2 kaleng soda dan 1 kaleng susu, sedangkan untuk membuat 1 liter minuman jenis B diperlukan 2 kaleng soda dan 3 kaleng susu. Tersedia 40 kaleng soda dan 30 kaleng susu. Jika 1 liter minuman jenis A dijual seharga Rp30.000,00 dan satu liter minuman jenis B dijual seharga Rp50.000,00, pendapatan maksimum dari hasil penjualan kedua jenis minuman tersebut adalah ….
A. Rp500.000,00
B. Rp540.000,00
C. Rp600.000,00
D. Rp700.000,00
E. Rp720.000,00
Pembahasan:
Misal banyak jenis minuman A adalah x dan banyak jenis minuman B adalah y. Maka dapat diperoleh sistem persamaan linear berikut.
x + y ≤ 20
x + 3y ≤ 30
x ≥ 0
y ≥ 0
Fungsi tujuan memaksimalkan f(x) = 30.000x + 50.000y
Perhatikan himpunan penyelesaian atau daerah layak yang sesuai dengan fungsi kendala sesuai soal cerita pada soal berikut.

Diperoleh empat titik pojok yaitu titik A (0, 0); B(0, 10); D(20, 0); dan titik C yang koordinatnya dapat dicari seperti cara berikut .

Mencari nilai maksimum f(x) = 30.000x + 50.000y untuk keempat titik.
A(0, 0) f(x) = 30.000 (0) + 50.000(0) = 0
B(0, 10) f(x) = 30.000 (0) + 50.000(10) = 500.000
C(15, 5) f(x) = 30.000 (15) + 50.000(5) = 700.000
D(20, 0) f(x) = 30.000 (20) + 50.000(0) = 600.000
Dari hasil perhitungan diperoleh nilai maksimum berada di titik C(15, 5) yaitu Rp700.000,00. Jadi, pendapatan maksimum dari hasil penjualan kedua jenis minuman tersebut adalah Rp700.000,00.
Jawaban: D
Demikianlah tadi ulasan bagaimana cara penyelesaian soal cerita program linear. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!
Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear Tiga Variabel (SPLTV)