Teorema sisa dan teorema faktor adalah dua teori untuk menyelesaikan masalah pembagian suku banyak (polinomial). Teorema sisa adalah konsep matematika yang menyatakan hubungan antara hasil bagi polinomial dan sisa pembagiannya. Sementara teorema faktor adalah lanjutan dari teorema sisa untuk menemukan faktor linier dari suatu polinomial.
Teorema sisa menyatakan bahwa jika kita membagi polinomial P(x) oleh (x – a) maka sisa pembagiannya sama dengan P(a). Secara matematis, teorema sisa dapat dinyatakan dalam persamaan P(x) = (x – a)· Q(x) + P(a) di mana Q(x) merupakan hasil bagi P(x) oleh (x – a).
Teorema faktor menyatakan bahwa jika a adalah akar dari suatu polinomial P(x), maka (x – a) adalah faktor dari P(x). Dengan kata lain, jika P(a) = 0 maka (x – a) adalah faktor dari P(x). Pernyataan teorema sisa secara matematis dinyatakan melalui persamaan P(x) = (x – a) · Q(x) di mana Q(x) adalah hasil bagi P(x) oleh (x – a).
Bagaimana cara menggunakan teorema sisa dan teorema faktor? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Baca Juga: Contoh Soal Jumlah dan Hasil Kali Akar-akar Polinomial
Teorema Sisa
Sebuah suku banyak (polinomial) memiliki persamaan f(x) = a0xn + a1xn–1 + a2xn–1 + … + an. Pembagian suku banyak tersebut oleh suatu fungsi suku banyak dengan bederajat yang lebih rendah akan menghasilkan sisa jika pembagi bukan merupakan faktor dari f(x).
Fungsi dari teorema sisa adalah sebuah cara untuk menentukan hasil bagi dari suatu pembagian suku banyak tapa melakukan pembagian terlebih dahulu.
Teorema sisa secara matematis dinyatakan dalam persamaan berikut.
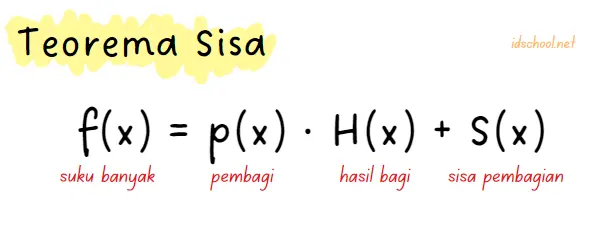
Untuk beberapa bentuk pembagi p(x), sisa pembagian S(x) menurut teorema sisa memenuhi persamaan-persamaan berikut.
- Jika suku banyak f(x) berderajat n dibagi dengan (x – k) maka sisanya adalah S(x) = f(k)
- Jika suku banyak f(x) berderajat n dibagi dengan (ax + b) maka sisanya adalah S(x) = f(–b/a)
- Jika suku banyak f(x) berderajat n dibagi dengan (x – a)(x – b) maka sisanya adalah
Contoh penggunaan teorema sisa terdapat pada langkah penyelesaian soal berikut.
Soal:
Tentukan sisa hasil bagi f(x) = x2 + 3x + 5 oleh x + 2!
Jawab:
Pada pembagian suku banyak, sisa dari pembagian f(x) = x2 + 3x + 5 oleh x + 2 dapat dicari menggunakan metode bersusun seperti berikut.
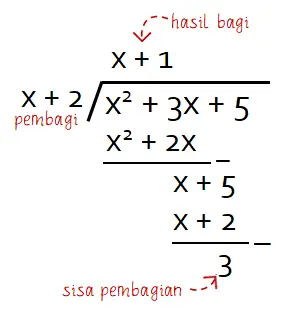
Namun itu bukan cara yang efektif karena teorema sisa bisa melakukannya dengan lebih cepat dan mudah.
Soal di atas dapat diselesaikan menggunakan teorema sisa untuk bentuk pembagi persamaan linear (x – k). Di mana jika suku banyak f(x) berderajat n dibagi dengan (x – k) maka sisanya adalah S(x) = f(k).
Pembagi suku banyak pada soal adalah (x + 2), nilai k dapat dicari menggunakan pembuat nol seperti berikut.
Menentukan pembuat nol pembagi suku banyak:
x + 2 = 0
x = ‒2, k = → ‒2
Berikutnya, susbtitusi nilai k = ‒2 pada f(x) = x2 + 3x + 5 untuk mendapatkan nilai sisa pembagian fungsi f(x) oleh (x + 2) seperti berikut.
Mencari sisa pembagian f(x) = x2 + 3x + 5 oleh x + 2:
S(x) = f(k) = f(‒2)
S(x) = (‒2)2 + 3(‒2) + 5
S(x) = 4 ‒ 6 + 5 = 3
Jadi, sisa hasil pembagian f(x) = x2 + 3x + 5 oleh x + 2 adalah S(x) = 3.
Baca Juga: Kesamaan Variabel pada Suku Banyak (Polinomial)
Teorema Faktor
Perluasan dari teorema sisa adalah teorema faktor. Teorema ini sangat berguna untuk mengetahui apakah pembagi suku banyak merupakan faktor dari suku banyak atau bukan secara lebih cepat.
Teorema Faktor:
Misalkan f(x) adalah suatu suku banyak dan (x – k) merupakan faktor dari f(x) jika dan hanya jika f(k) = 0.
Dari teorema faktor dapat dipahami bahwa saat f(k) = 0 maka (x – k) merupakan faktor dari f(x). Lalu bagaimana jika f(x) ≠ 0? Ya tentu saja kesimpulannya adalah (x – k) bukan merupakan faktor dari f(x).
Bagaimana penggunaan teorema faktor terdapat pada langkah penyelesaian soal di bawah.
Soal:
Apakah (x – 1) merupakan faktor dari f(x) = x3 ‒ 3x2 + 3x ‒ 1?
Pembahasan:
Faktor dari suatu suku banyak dapat membagi habis suku banyak (sisa pembagian sama dengan nol). Untuk melihat hasil pembagian dan sisa pembagian (jika ada) dari f(x) = x3 ‒ 3x2 + 3x ‒ 1 oleh (x – 1) dapat menggunakan cara bersusun seperti berikut.
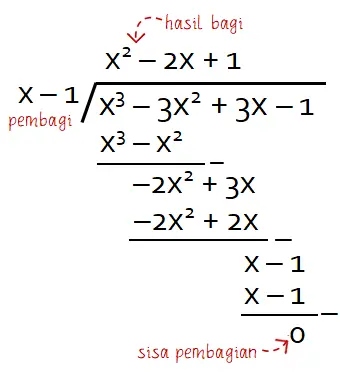
Dapat diketahui bahwa sisa hasil pembagian suku banyak sama dengan nol. Sehingga dapat disimpulkan bahwa (x ‒ 1) merupakan faktor dari f(x) = x3 ‒ 3x2 + 3x ‒ 1.
Tentu saja cara di atas tidak cukup praktis karena ada cara yang lebih mudah yaitu menggunakan teorema faktor.
Dengan teroema faktor hanya perlu substitusi nilai x pembuat nol dari pembagi suku banyak. Jika hasilnya sama dengan nol maka pembagi tersebut merupakan faktor dari suku banyak. Jika hasil tidak nol (memiliki sisa) maka pembagi tersebut bukan merupakan faktor dari suku banyak.
Menentukan pembuat nol pembagi suku banyak:
x ‒ 1 = 0
x = 1, k = → 1
Berikutnya substitusi nilai k pada fungsi f(x) untuk melihat hasil nilainya seperti cara berikut.
Substitusi nilai k:
f(x) = x3 ‒ 3x2 + 3x ‒ 1
f(1) = (1)3 ‒ 3(1)2 + 3(1) ‒ 1
f(1) = 1 ‒ 3 + 3 ‒ 1 = 0
Diperoleh hasil substitusi sama dengan nol. Dengan demikian dapat disimpulkan bahwa (x ‒ 1) merupakan faktor dari f(x) = x3 ‒ 3x2 + 3x ‒ 1.
Baca Juga: Cara Melakukan Pemfaktoran Persamaan Kuadrat
Contoh Soal Teorema Sisa dan Teorema Faktor + Bahas
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman teorema sisa dan teorema faktor. Setiap soal yang diberikan dilengkapi dengan pembahasannya.
Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh – 1
Suatu suku banyak f(x) dibagi x ‒ 1 sisa 2, dibagi x ‒ 2 sisa 3. Suatu suku banyak g(x) dibagi x ‒ 1 sisa 5, dibagi x ‒ 2 sisa 4. Jika h(x) = f(x) ∙ g(x), maka sisa pembagian h(x) oleh x2 ‒ 3x + 2 adalah ….
A. ‒2x + 12
B. ‒2x + 8
C. ‒x + 4
D. 2x + 8
E. x + 4
Pembahasan:
- Dari informasi yang diberikan pada soal dapat diketahui:
- f(x) dibagi x ‒ 1 sisa 2
- f(x) dibagi x ‒ 2 sisa 3
- g(x) dibagi x ‒ 1 sisa 5
- g(x) dibagi x ‒ 2 sisa 4
- h(x) = f(x) ∙ g(x)
Misalkan Q(x) dan S(x) = ax + b berturut-turut adalah hasil bagi dan sisa hasil bagi dari suku banyak h(x) oleh x2 ‒ 3x + 2. Berdasarkan teorema sisa, suku banyak h(x) akan memenuhi persamaan berikut.
h(x) = (x2 ‒ 3x + 2) ∙ Q(x) + S(x)
h(x) = (x ‒ 2)(x ‒ 1) ∙ Q(x) + ax + b
Dari persamaan suku banyak h(x) = (x ‒ 2)(x ‒ 1) ∙ Q(x) + S(x) diketahui bahwa bentuk pembaginya adalah (x ‒ 2)(x ‒ 1). Sehingga dapat bentuk dua persamaan berikut.
Persamaan 1: h(1) = Sf(x)(1) ∙ Sg(x)(1)
(1 ‒ 2)(1 ‒ 1) ∙ H(1) + (a ∙ 1 + b) = 2 ∙ 5
‒1 ∙ 0 ∙ H(1) + a + b = 10
a + b = 10
Persamaan 2: h(2) = Sf(x)(2) ∙ Sg(x)(2)
(2 ‒ 2)(2 ‒ 1) ∙ H(2) + ( a ∙ 2 + b) = 3 ∙ 4
0 ∙ 1 ∙ H(2) + 2a + b = 12
2a + b = 12
Diperoleh dua persamaan yaitu a + b = 10 dan 2a + b = 12. Nilai a dan b dapat dicari menggunakan metode substitusi atau metode eliminasi pada penyelesaian sistem persamaan linear dua variabel (spldv).
Mencari nilai a:
Eliminasi b dari persamaan 1 dan 2.
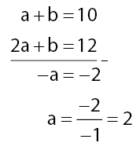
Mencari nilai b: substitusi nilai a = 2 pada persamaan a + b = 10 (atau 2a + b = 12).
2 + b = 10
b = 10 ‒ 2 = 8
Diperoleh nilai a = 2 dan b = 8, serta telah dimisalkan S(x) = ax + b. Sehingga sisa pembagian h(x) oleh x2 ‒ 3x + 2 adalah S(x) = ax + b = 2x + 8.
Jadi, sisa pembagian h(x) oleh x2 ‒ 3x + 2 adalah 2x + 8.
Jawaban: D
Contoh – 2
Suku banyak F(x) = x3 – (a – 1)x2 + bx + 2a. Jika F(x) dibagi oleh (x – 2) mempunyai sisa 4 dan tidak mempunyai sisa jika F(x) dibagi (x + 2). Nilai a dan b berturut-turut adalah ….
A. –1 dan –3
B. –1 dan –1
C. –1 dan 3
D. 1 dan –3
E. 1 dan 3
Pembahasan:
- Berdasarkan keterangan pada soal diketahui bahwa:
- F(x) = x3 – (a – 1)x2 + bx + 2a
- F(x) dibagi (x – 2) mempunyai sisa 4
- F(x) dibagi (x + 2) tidak memiliki sisa
Dari informasi yang diberikan tersebut dapat dibentuk dua persamaan berdasarkan teorema sisa dan teorema faktor seperti berikut.
Persamaan 1: F(x) dibagi (x – 2) mempunyai sisa 4
F(2) = 23 – (a – 1) · 22 + b · 2 + 2a = 4
8 – 4a + 4 + 2b + 2a = 4
2a – 2b = 8
a – b = 4 → a = b + 4
Persamaan 2: F(x) dibagi (x + 2) tidak memiliki sisa (sama dengan nol).
F(–2) = (–2)3 – (a–1)·(–2)2 + b·(–2)+2a = 0
–8 – 4a + 4 – 2b + 2a = 0
–2a – 2b = 4
a + b = –2
Diperoleh dua persamaan yaitu a = b + 4 dan a + b = –2. Nilai a dan b dapat dicari tahu dengan menyelesaikan sistem persamaan linear dua variabel tersebut.
Menentukan nilai b:
Substitusi a = b + 4 ke persamaan a + b = –2 sehingga dapat diperoleh nilai b seperti berikut.
b + 4 + b = –2
2b = –2 – 4
2b = –6
b = –6/2 = –3
Menentukan nilai a:
a = –3 + 4
a = 1
Jadi, nilai a dan b berturut-turut adalah 1 dan –3.
Jawaban: D
Sekian pembahasan mengenai teorema sisa dan teorema faktor suku banyak. Terima kasi sudah menyimak ulasan teorema sisa dan teorema faktor sampai akhir, semoga bermanfaat!
