Gradien adalah nilai kemiringan garis lurus. Lambang gradien dituliskan menggunakan huruf m. Cara menentukan gradien cukup mudah. Jika tahu caranya. Nilai gradien garis y = 2x + 3 adalah m = 2. Nilai gradien garis y = −3x + 2 adalah m = −3. Dari mana nilai gradien itu diperoleh? Akan dijelaskan melalui bahasan di bawah.
Daftar isi:
Baca Juga: Rumus Persamaan Garis Lurus
Rumus Gradien
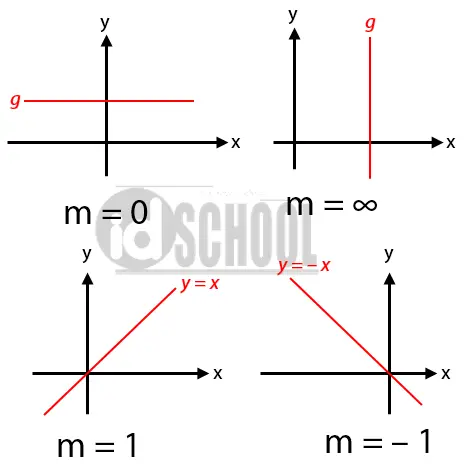
Nilai gradien menyatakan perbandingan perubahan sumbu vertikal (Δy) dengan sumbu horizontal (Δx). Rumus gradien adalah m = Δy/Δx. Garis lurus horizontal memiliki gradien m = 0 karena Δy = 0. Sementara gradien garis lurus vertikal adalah m = ∞ karena Δx = 0.
Garis yang condong ke kanan memiliki nilai gradien positif. Sementara garis yang condong ke kiri memiliki nilai gradien negatif.
Garis lurus yang condong ke kanan dengan kemiringan 45o memiliki gradien m = 1. Sedangkan garis lurus yang condong ke kiri dengan kemiringan 45o memiliki nilai gradien m = −1.
Baca Juga: Persamaan Garis yang Saling Sejajar
Cara Menentukan Gradien Garis Lurus
Ada empat cara untuk menentukan gradien. Penjelasan empat cara menentukan gradien ada di bawah.
1) Diberikan sebuah gambar
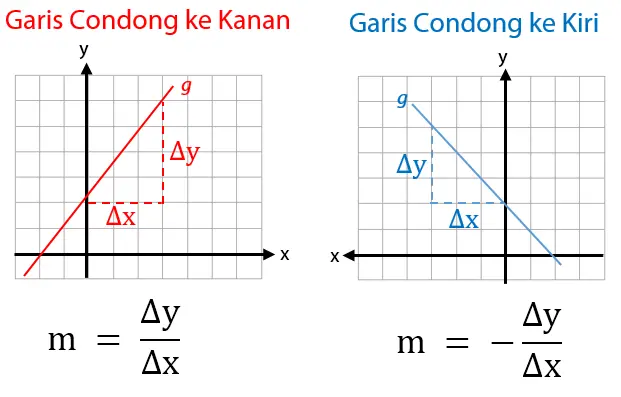
Dari sebuah gambar, dapat dilihat kemana arah condongnya. Jika garis condong ke kanan, nilai gradien positif (+). Jika garis condong ke kiri, nilai gradien negatif (–).
Besar nilainya adalah perbandingan selisih sumbu y (Δy) dan sumbu x (Δx). Untuk mengetahui nilai selisih sumbu x dan sumbu y, buat garis proyeksi seperti berikut.
Sebagai contoh, perhatikan cara menentukan gradien garis lurus dari gambar berikut.
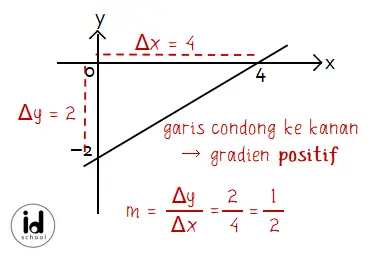
Dari gambar, garis diketahui condong ke kanan. Sehingga nilai gradiennya adalah positif. Nilai Δy = 2 dan Δx = 4, sehingga gradien garis lurus tersebut adalah m = 2/4 = 1/2.
2) Diketahui persamaan y = mx + c
Garis y = mx + c memiliki nilai gradien = m. Yaitu sebuah angka di depan variabel x. Misalkan sebuah garis lurus memiliki persamaan y = 2x + 4. Angka di depan variabel x adalah 2. Sehingga gradien garis lurus tersebut adalah m = 2.

Untuk garis dengan persamaan qy = px + c. Rumus gradiennya adalah koefisien x per koefisien y. Sehingga, gradien garis lurus qy = px + c adalah m = p/q.
Rumus gradien garis qy = px + c:
Sebagai contoh, garis lurus 2y = 3x + 5 memiliki nilai gradien m = 3/2.
Baca Juga: Cara Mencari Persamaan Garis yang Saling Tegak Lurus
3) Diketahui persamaan Ax + By + C = 0
Garis Ax + By + c = 0 memiliki nilai gradien m = –A/B. Sebagai contoh, garis 3x + 2y – 6 = 0. Nilai A = angka di depan variabel x, A = 3. Nilai B = angka di depan variabel y, B = 2. Jadi, gradien garis 3x + 2y – 6 = 0 adalah m = –3/2 = –11/2 .

Untuk garis Ax + By = C juga dapat menggunakan rumus gradien ini. Misalkan sebuah garis garis x – 3y = 5. Gradien garis tersebut adalah m = 1/–3 = –1/3.
4) Diketahui 2 Titik
Diketahui garis PQ melalui dua titik yaitu P(x1, y1) dan Q(x2, y2). Rumus gradien garis PQ adalah m = Δy/Δx = y2-y1/x2-x1. Atau, gradien PQ = y1-y2/x1-x2.
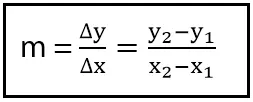
Sebagai contoh, sebuah garis lurus melalui titik A(1, 2) dan B(2, 1). Gradien garis tersebut dapat dicari dengan cara berikut.
Sifat Gradien Dua Garis Lurus
Dua garis lurus dapat saling sejajar atau saling tegak lurus. Sifat gradien garis lurus yang saling sejajar dan tegak lurus ada di bawah.
1) Dua garis lurus saling sejajar
Garis lurus yang saling sejajar adalah garis-garis yang tidak memiliki titik potong. Sifat gradien garis lurus yang saling sejajar adalah sama.

Misalkan garis g sejajar dengan garis h. Diketahui gradien garis g adalah mg = 2. Dengan sifat gradien garis saling sejajar. Gradien garis h dapat diketahui, yaitu mh = 2.
2) Dua garis lurus saling tegak lurus
Garis lurus yang saling tegak lurus adalah garis yang berpotongan dan mebentuk sudut siku-siku. Sifat gradien garis lurus yang saling tegak lurus memilki hasil perkalian sama dengan –1.

Misalkan garis g tegak lurus dengan garis h. Diketahui gradien garis g adalah mg = 2. Dengan sifat gradien garis saling sejajar. Gradien garis h dapat diketahui, yaitu mh = –1/2.
Baca Juga: Rumus Jarak Titik ke Garis
Contoh Soal Gradien
Latihan soal menentukan gradien ada di bawah!
Contoh 1 – Diberikan gambar
Sebuah tangga bersandar pada dinding tembok (seperti pada gambar).
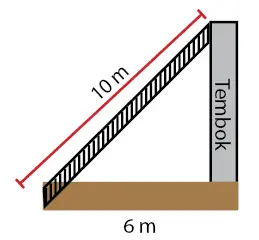
Kemiringan tangga terhadap dinding tembok adalah ….
A. 4/3
B. 5/4
C. 4/5
D. 3/4
Pembahasan:
Kemiringan tangga sama dengan nilai gradien. Tangga condong ke kanan, sehingga kemiringannya bernilai positif (+).
Selisih sumbu x (horizontal) adalah Δx = 6 m. Sementara selisih sumbu y (Δy) belum diktahui. Sehingga perlu dihitung terlebih dahulu. Caranya menggunakan Pythagoras.
Menghitung tinggi tembok (Δy):
ttembok = √(102 – 62)
ttembok = √(100 – 36) = √64 = 8 m
Diperoleh nilai ttembok = Δy = 8 m. Jadi, kemiringan tangga terhadap dinding tembok adalah m = Δy/Δx = 8/6 = 4/3.
Jawaban: A
Contoh 2 – Diketahui 2 titik
Gradien dari sebuah garis yang melalui titik P(1, 3) dan Q(5, 7) adalah ….
A. 2
B. 1
C. 0
D. –1
Pembahasan:
Rumus gradien saat diketahui garis yang melalui dua titik.
Sehingga,
Jadi, gradien dari sebuah garis yang melalui titik P(1, 3) dan Q(5, 7) adalah m = 1.
Jawaban: B
Contoh 3 – Gradien garis yang nilainya sama
Diketahui:
(i) y = 3x – 10
(ii) x + 3y = 6
(iii) 3x – y + 12 = 0
(iv) 3x + y = 6
Pasangan garis yang mempunyai gradien sama adalah ….
A. (i) dan (ii)
B. (i) dan (iii)
C. (ii) dan (iii)
D. (ii) dan (iv)
Pembahasan:
Cara menentukan gradien garis lurus ada di bawah.
(i) y = 3x – 10 → gunakan cara 2)
m = koefisien x = 3
(ii) x + 3y = 6 → gunakan cara 3)
m = –A/B = –1/3
(iii) 3x – y + 12 = 0 → gunakan cara 3)
m = –A/B = –3/(–1) = 3
(iv) 3x + y = 6 → gunakan cara 3)
m = –A/B = –3/1 = –3
Garis y = 3x – 10 dan 3x – y + 12 = 0 memiliki nilai gradien yang sama yaitu m = 3. Jadi, pasangan garis yang mempunyai gradien sama adalah (i) y = 3x – 10 dan (iii) 3x – y + 12 = 0.
Jawaban: B
Contoh 4 – Sifat gradien garis
Perhatikan gambar dan pernyataan berikut!

(1) Kemiringan garis g = –3/4
(2) Kemiringan garis h = –4/3
(3) Persamaan garis g adalah 3x – 4y = –24
(4) Persamaan garis h adalah 4x – 3y = 6
Pernyataan yang benar adalah ….
A. (1) dan (3)
B. (1) dan (4)
C. (2) dan (3)
D. (2) dan (4)
Pembahasan:
Pertama, gradien garis g dapat dicari karena selisih sumbu x dan sumbu y diketahui secara pasti.
Pernyataan (1):
Garis g condong ke kanan (gradien positif), Δx = 8, dan Δy = 6. Sehingga gradien garis g dicari dengan cara berikut.
Pernyataan (2):
Diketahui bahwa garis h tegak lurus dengan garis g. Dua garis yang saling tegak lurus memiliki sifat perkalian gradien = –1.
Sehingga,
mg × mh = –1
Pernyataan (3):
Garis g diketahui melalui dua titik, yaitu (–8, 0) dan (0, 6). Persamaan garis g dicari menggunakan rumus garis lurus yang melalui 2 titik seperti berikut.
3(x + 8) = 4y
3x + 24 = 4y
3x – 4y = –24 → Pernyataan (3) Benar
Pernyataan (4):
Garis h diketahui memiliki gradien garis mh = –4/3 dan melalui titik (0, –2). Persamaan garisnya dicari menggunakan rumus y – y1 = mh(x – x1).
Sehingga,
y – (–2) = –4/3(x – 0)
y + 2 = –4/3x
3(y + 2) = –4x
3y + 6 = –4x
4x + 3y = –6 → Pernyataan (4) Salah
Jadi, pernyataan yang benar adalah (2) dan (3).
Jawaban: C.
Sekian ulasan cara menentukan gradien garis lurus beserta contohnya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
plz makasi bgt ini sangat membantu
Terima kasih kak🙏🙏
trims
Halo D, terimkasih atas kunjungannya
Terima kasih, semoga sukses dan berkah.
Halo Ferdi, terimakasih do’a nya, do’a yang sama juga untuk Ferdi.
Terimakasih…sangat membantu
Halo Wien, terimakasih juga atas kunjungannya.