Pesawat sederhana banyak digunakan untuk mempermudah pekerjaan manusia. Hal ini dikarenakan pesawat sederhana memiliki nilai keuntungan mekanis. Keuntungan mekanis pesawat sederhana menunjukkan besar nilai keuntungan penggandaan gaya karena menggunakan pesawat sederhana. Ada tiga jenis pesawat sederhana yang terdiri dari tuas/pengungkit, katrol, dan bidang miring. Besar keuntungan mekanis pesawat sederhana untuk ketiga jenis dapat diperoleh dari perbandingan antar berat benda yang diangkat dan gaya yang diberikan pada benda.
Fungsi utama dari penggunaan pesawat sederhana adalah untuk meringankan pekerjaan. Besar keuntungan mekanis pesawat sederhana sama dengan perbandingan antara beban yang diangkat dan besar gaya/kuasa yang dibutuhkan. Nilai tersebut juga sama dengan perbandingan lengan kuasa dan lengan beban.

Baca Juga: Cara Membaca Jangka Sorong (Alat Ukur Panjang)
Bagaimana cara mencari besar keuntungan mekanis pesawat sederhana? Simak lanjutan ulasan keuntungan mekanis pesawat sederaha pada bahasan di bawah.
Table of Contents
Keuntungan Mekanis Tuas/Pengungkit
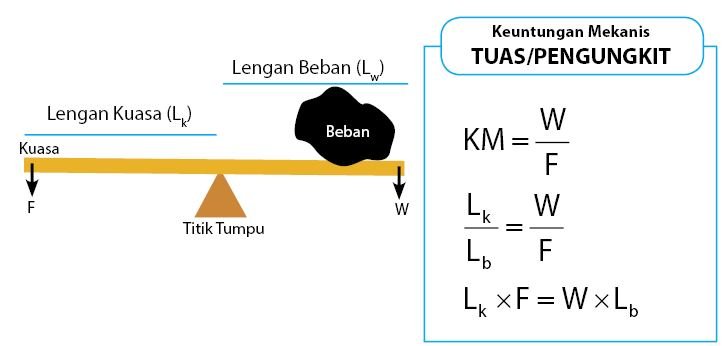
Pembahasan keuntungan mekanis pesawat sederhana pertama adalah jenis pesawat sederhana yang termasuk dalam tuas atau pengungkit. Tuas atau pengungkit memiliki tiga titik yaitu titik tumpu, beban, dan kuasa. Jarak antara titik beban dengan titik tumpu disebut lengan beban. Sedangkan jarak antara titik kuasa dengan titik tumpu disebut lengan kuasa.
Tuas dikelompokkan menjadi 3 (tiga) pengelompokan berdasarkan letak kuasa, titik tumpu, dan beban. Kelompok pertama adalah jenis tuas dengan letak titik tumpu yang berada di tengah. Jenis kedua adalah kelompok tuas dengan letak titik beban pada bagian di tengah. Sedangkan jenis tuas yang ketiga adalah pengungkit dengan titik kuasa yang terletak di tengah.
Besar keuntungan mekanis tuas/pengungkit diberikan melalui persamaan di bawah.
Contoh Soal Keuntungan Mekanis Tuas dan Pembahasan
Sebatang bambu sepanjang 2 meter digunakan sebagai pengungkit untuk memindahkan sebongkah batu seberat 360 N. Pada bambu diletakkan penumpu yang berjarak 20 cm dari batu. Besar kuasa minimal yang harus diberikan pada ujung bambu yang lain agar batu terangkat….
A. 40 N
B. 60 N
C. 80 N
D. 100 N
Pembahasan:
Berdasarkan informasi pada soal, dapat diketahui bahwa:
- W (berat batu) = 360 N
- L (panjang kayu) = 2 m
- Lb (lengan beban) = 20 cm = 0,2 m
Sehingga:
Lk = L – Lb
Lk = 2 – 0,2 = 1,8 m
Besar kuasa yang diperlukan untuk mengagnkat batu adalah

Jadi, besar kuasa minimal yang harus diberikan pada ujung bambu yang lain agar batu terangkat adalah 40 N.
Jawaban: A
Baca Juga: Kaidah Tangan Kanan
Keuntungan Mekanis Katrol
Seperti halnya dengan keuntungan mekanis pesawat sederhana jenis tuas, keuntungan mekanis katrol dinyatakan melalui perbandingan beban dan kuasa. Sama seperti pada tuas, katrol juga memiliki titik beba, kuasa, dan titik tumpu. Perhatikan posisi letak titik tumpu, beban, kuasa, serta lengan beban dan lengan kuasa pada 2 jenis katrol berikut.
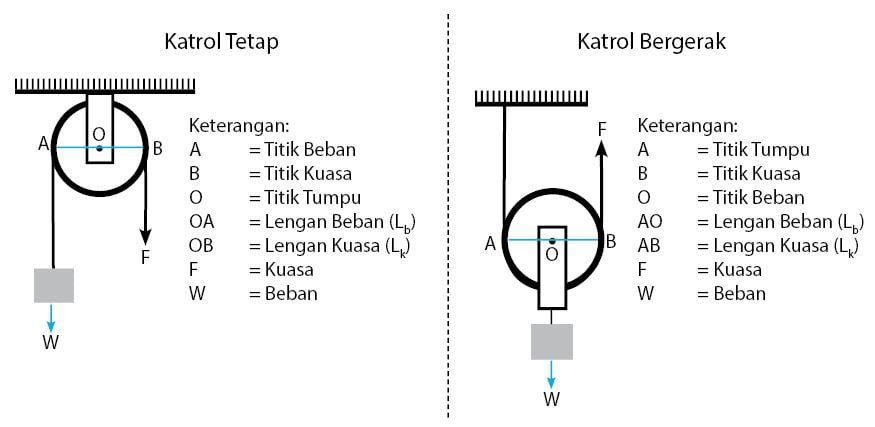
Pada umumnya, ada tiga jenis katrol yang digunakan pada kehidupan sehari-hari, yaitu katrol tetap, katrol bebas, dan katrol bergerak. Dalam katrol, nilai keuntungan mekanis dari tiga jenis katrol tersebut berbeda. Berikut ini adalah nilai keuntungan mekanis dari 3 jenis katrol.
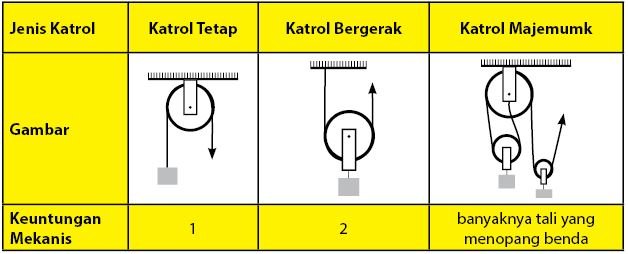
Besar keuntungan mekanis katrol:
- Keuntungan mekanis katrol tetap: KM = 1 (satu)
- Keuntungan mekanis katrol bergerak: KM = 2 (dua)
- Pada katrol ganda/katrol majemuk memiliki nilai keuntungan mekanis sama dengan sejumlah banyak tali yang menopang benda.
Contoh Soal Keuntungan Mekanis Katrol dan Pembahasan
Sebuah benda yang beratnya 200 N diangkat menggunakan katrol bergerak. Gaya yang diperlukan untuk mengangkat beban tersebut adalah ….
A. 50 N
B. 100 N
C. 200 N
D. 400 N
Pembahasan:
Keuntungan mekanis bergerak sama dengan 2, sehingga besar gaya yang dibutuhkan untuk mengangkat beban dapat dihitung seperti berikut.

Jadi, besar gaya yang dibutuhkan untuk mengangkat beban seberat 200 N adalah 100 N.
Jawaban: B
Baca Juga: Keuntungan Menggunakan Pesawat Sederhana
Keuntungan Mekanis Bidang Miring
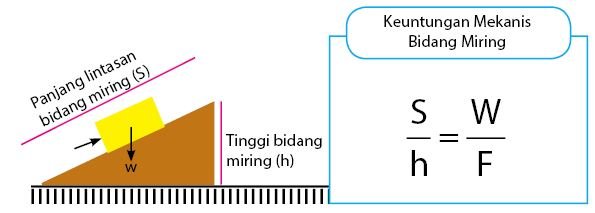
Nilai keuntungan mekanis pesawat sederhana berbentuk bidang miring sama juga menggunakan perbandingan berat dan kuasa. Selain itu, nilai keuntungan mekanis bidang miring juga akan sebanding dengan nilai perbandingan jarak lintasan bidang miring dan ketinggian bidang miring.
Persamaan keuntungan mekanis pesawat sederhana berbentuk bidang miring sesuia dengan persamaan di bawah.
Contoh Soal Keuntungan Mekanis Bidang Miring dan Pembahasan
Perhatikan gambar di bawah!

Besar gaya yang dibutuhkan untuk menaikkan barang seberat 600 N menggunkan bidang miring di atas adalah ….
A. 100 N
B. 200 N
C. 600 N
D. 1.200 N
Pembahasan:
Menghitung besar gaya yang dibutuhkan:
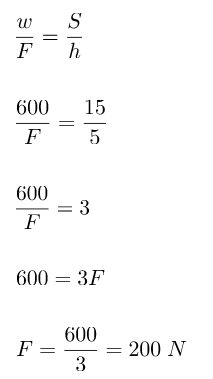
Besar gaya yang dibutuhkan untuk menaikkan barang seberat 600 N menggunkan bidang miring tersebut adalah 200 N.
Jawaban: B
Demikianlah ulasan tentang keuntungan mekanis pesawat sederhana yang terdiri dari keuntungan mekanis pesawat sederhana berbentuk tuas/pengungkit, katrol, dan bidang miring. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Sistem Katrol Majemuk
Apakah ada soal yg Lain