Parabola merupakan kurva yang mewaikili persamaan kuadrat. Bentuk kurvanya dapat melengkung ke atas, bawah, kanan, atau kiri. Parabola merupakan salah satu dari hasil irisan kerucut. Sebelumnya, telah diulas mengenai bentuk umum persamaan parabola. Halaman ini akan membahas bagaimana menentukan kedudukan garis terhadap parabola.
Kedudukan garis terhadap parabola dapat terjadi untuk 3 (tiga) kondisi. Ketiga kondisi tersebut adalah garis tidak memotong parabola, garis menyinggung parabola, dan garis memotong parabola pada dua titik. Tiga kondisi tersebut dapat dilihat lebih jelas lagi seperti gambar di bawah.

Untuk menentukan kedudukan garis terhadap parabola, sobat idschool perlu mengingat kembali apa yang dimaksud diskriminan pada persamaan kuadrat. Diskriminan adalah hubungan antara koefisien dalam persamaan kuadrat untuk mencari hubungan kedudukan garis terhadap parabola.
Jika diketahui persamaan kuadrat y = ax2 + bx + c maka nilai diskriminannya dapat diperoleh melalui rumus D = b2 − 4ac.
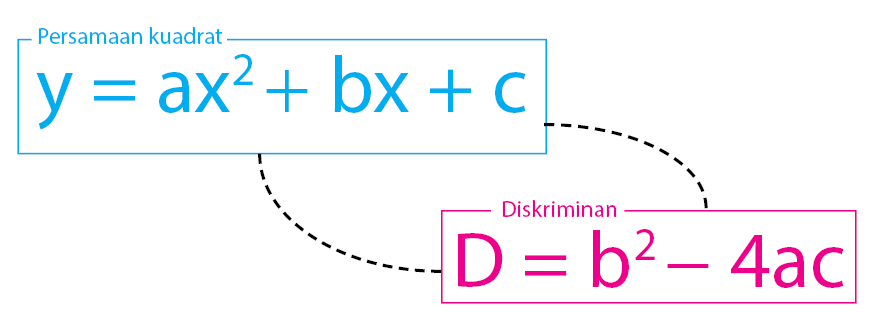
Baca Juga: Kedudukan Titik Terhadap Parabola
Setelah mengetahui cara mencari nilai diskriminan, sobat idschool perlu mengikuti langkah-langkah berikut untuk menentukan bagaimana kedudukan garis terhadap parabola.
Langkah-langkah menentukan kedudukan garis terhadap parabola:
- Substitusi persamaan garis lurus by = ax + c ke persamaan parabola sehingga akan diperoleh persamaan akhir berupa persamaan kuadrat.
- Menentukan nilai diskriminan (D) dari persamaan kuadrat yang diperoleh pada poin pertama.
- Menyimpulkan hasilnya, apakah garis tidak memotong parabola, garis menyinggung parabola, atau garis memotong parabola di dua titik.
Pembahasan lebih jelasnya akan diberikan pada ulasan materi di bawah. Untuk ulasan materi pertama yang akan dibahas adalah garis tidak memotong parabola.
Table of Contents
- Garis tidak memotong parabola
- Garis memotong parabola di satu titik (menyinggung parabola)
- Garis memotong parabola di dua titik
Garis tidak memotong parabola
Ulasan materi pertama yang akan dibahas adalah kriteria garis yang tidak memotong parabola. Sebuah garis dikatakan tidak memotong parabola jika garis dan parabola terpisah dan tidak mempunyai satu titik potong pun. Kondisi ini terjadi ketika nilai diskriminannya kurang dari nol.
Perhatikan gambar di bawah!

Contoh soal dan pembahasan menentukan garis tidak memotong parabola.
Soal:
Tentukan kedudukan garis lurus dengan persamaan y = x – 3 pada persamaan parabola x2 = 2(y – 1).
Jawab:
Langkah pertama yang harus dilakukan adalah substitusi persamaan garis lurus y = x – 3 pada persamaan parabola x2 = 2(y – 1).
x2 = 2(y – 1)
x2 = 2(x – 3 – 1)
x2 = 2(x – 4)
x2 = 2x – 8
x2 – 2x + 8 = 0
Berdasarkan persamaan kuadrat di atas, dapat diperoleh bahwa nilai a = 1, b = –2, dan c = 12. Selanjutnya, akan dicari nilai diskriminannya.
D = b2 – 4ac
D = (–2)2 – 4 × 1 × 12
D = 4 – 48 = – 44
Hasil perhitungan diskriminannya adalah kurang dari 0 (D < 0), sehingga dapat disimpulkan bahwa garis tersebut tidak memotong parabola. Untuk membuktikannya, dapat dilihat gambar parabola dan garis yang diberikan di bawah.

Berikutnya, ulasan materi yang akan disampaikan adalah kriteria garis memotong parabola pada satu titik, atau yang biasa disebut juga dengan garis menyinggung parabola.
Baca Juga: Persamaan Garis Singgung Parabola
Garis memotong parabola di satu titik (menyinggung parabola)
Materi kedua dari kedudukan garis terhadap parabola adalah garis memotong parabola pada satu titik (menyinggung parabola). Suatu garis yang menyinggung parabola hanya memiliki satu titik potong. Jika dilihat dari nilai diskriminannya, hasil perhitungan dari diskriminan akan menghasilkan 0 (nol).
Perhatikan gambar di bawah!

Contoh soal dan pembahasan menentukan garis tidak memotong parabola.
Soal:
Tentukan kedudukan garis lurus dengan persamaan y = x + 3 pada persamaan parabola (y – 2)2 = 8(x – 1).
Jawab:
Langkah pertama yang harus dilakukan adalah substitusi persamaan garis lurus y = x + 3 pada persamaan parabola (y – 2)2 = 8(x – 1).
(y – 2)2 = 8(x – 1)
(x + 3 – 2)2 = 8(x – 1)
( x + 1)2 = 8(x – 1)
x2 + 2x + 1 = 8x – 8
x2 + 2x – 8x + 1 + 8 = 0
x2 – 6x + 9 = 0
Berdasarkan persamaan kuadrat di atas, dapat diperoleh bahwa nilai a = 1, b = –6, dan c = 9. Selanjutnya, akan dicari nilai diskriminannya (D).
D = b2 – 4ac
D = (–6)2 – 4(1)(9)
D = 36 – 36 = 0
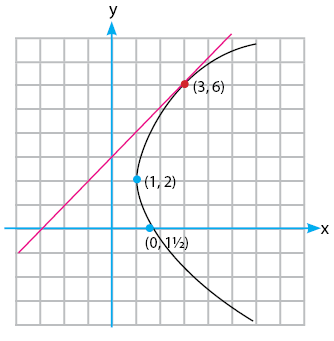
Hasil perhitungan diskriminannya adalah sama dengan 0 (D = 0), sehingga dapat disimpulkan bahwa garis tersebut memotong parabola pada satu titik (menyinggung parabola).
Langkah di atas sudah cukup untuk menentukan kedudukan garis terhadap parabola untuk garis menyinggung parabola. Berikut ini adalah gambar yang sesuai dengan kondisi pada soal yang diberikan di atas.
Baca Juga: Irisan Kerucut Bentuk Parabola
Garis memotong parabola di dua titik
Garis memotong parabola di dua titik artinya memiliki dua titik yang sama-sama dilalui, baik oleh parabola atau garis lurus. Sebuah garis akan memiliki dua titik potong jika memiliki nilai diskriminan lebih dari 0 (nol). Berikut ini adalah kriteria garis memotong parabola pada dua titik.

Contoh soal dan pembahasan menentukan garis memotong parabola di dua titik.
Soal:
Tentukan kedudukan garis lurus dengan persamaan y = 2x + 1 pada persamaan parabola x2 = 2(y – 1).
Jawab:
Langkah pertama yang harus dilakukan adalah substitusi persamaan garis lurus y = 2x + 1 pada persamaan parabola x2 = 2(y – 1).
x2 = 2(y – 1)
x2 = 2(2x + 1 – 1) \]
x2 = 4x
x2 – 4x = 0
Berdasarkan persamaan kuadrat di atas, dapat diperoleh bahwa nilai a = 1, b = –4, dan c = 0. Selanjutnya, akan dicari nilai diskriminannya.
D = b2 – 4ac
D = (- 4)2 – 4(1)(0)
D = 16 + 0 = 16
Hasil perhitungan diskriminannya adalah lebih dari 0 (D >0). Sehingga dapat disimpulkan bahwa garis tersebut memotong parabola pada dua titik.
Langkah di atas sudah cukup untuk menentukan kedudukan garis terhadap parabola, namun untuk membuktikannya, dapat dilihat gambar parabola dan garis, sesuai yang diberikan pada soal.

Terlihat bukan, bahwa garis memotong parabola pada dua titik. Rangkuman ketiga kriteria kedudukan garis terhadap parabola dapat dilihat pada tabel di bawah.

Sekian pembahasan mengenai kedudukan garis terhadap parabola. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Irisan Kerucut (Lingkaran, Elips, Parabola, Hiperbola)