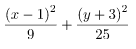Sebuah elips yang terletak pada bidang kartesius memiliki persamaan umum elips. Persamaan tersebut merupakan representasi elips dalam sebuah persamaan. Ulasan materi pada halaman ini, akan dibahas kedudukan titik terhadap elips, yang meliputi di dalam elips, pada elips, dan di luar elips.
Sebelumnya, bayangkan sebuah elips dan sebuah titik yang terletak pada bidang kartesius yang sama. Kedudukan titik pada elips tersebut pastinya akan membentuk sebuah hubungan. Hubungan tersebut dapat berupa kedudukan titik di dalam elips, kedudukan titik pada elips, dan kedudukan titik di luar elips. Seperti terlihat pada gambar di bawah.

Pada gambar pertama, titik terlihat terletak di dalam luas wilayah elips. Gambar kedua menunjukkan bahwa titik tepat berada pada garis batas elips. Sedangkan gambar ketiga menunjukkan bawah titik berada di luar elips. Dengan melihat kedudukan titik pada elips melalui gambar, akan secara mudah ditentukan kedudukan titik terhadap elips.
Namun, bagaimana jika yang diketahui hanya persamaan elips dan letak koordinat sebuah titik?

Menentukan kedudukan titik terhadap elips dengan cara menggambarkan elips dari persamaan yang diketahui kemudian melihat letak titik lingkaran yang diketahui letak koordinatnya, tentu bukan merupakan cara yang efektif.
Baca Juga: Kedudukan titik terhadap lingkaran
Melalui halaman ini, sobat idschool akan belajar menentukan kedudukan titik terhadap elips yang diketahui persamaannya dan sebuah titik yang diketahui letak koordinatnya. Pastinya, tanpa menggambarkannya terlebih dahulu pada bidang kartesius.
Table of Contents
Kedudupan Titik di Dalam Elips
Ulasan yang pertama akan dibahas adalah kriteris titik yang terletak di dalam elips. Sebuah titik akan terletak di dalam elips jika hasil hitung dari substitusi nilai titik ke persamaan elips menghasilkan nilai kurang dari satu. Lebih jelasnya perhatikan kriteria di bawah.

Contoh 1 soal menentukan kedudukan titik terhadap elips
Tentukan kedudukan titik (1, 1) pada elips dengan persamaan berikut!
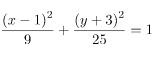
Pembahasan:
Substitusi titik (1, 1) pada persamaan elips, sehingga akan diperoleh perhitungan sebagai berikut.
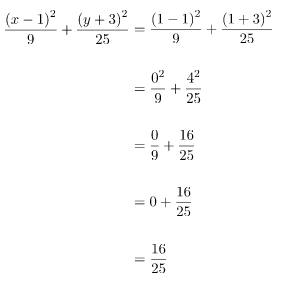
Diperoleh hasil perhitungannya adalah 16/25, nilainya kurang dari satu (< 1 ). Sehingga, tanpa menggambarnya terlebih dahulu, dapat disimpulkan bahwa titik (1, 1) terletak di dalam elips.
Untuk melihat kebenarannya, perhatikan gambar elips dan letak titik sesuai pada soal yang diberikan.
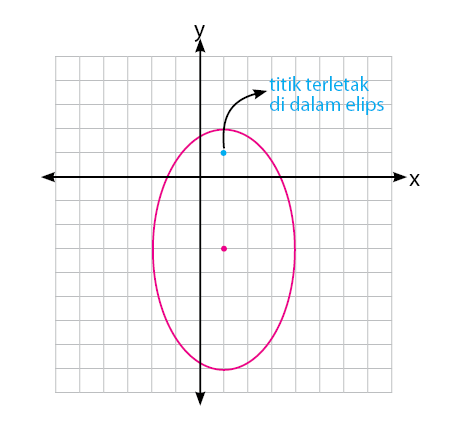
Terlihat bahwa titik terletak di dalam elips. Selanjutnya adalah letak titik terhadap elips untuk kasus ke dua, yaitu titik terletak pada elips.
Kedudukan Titik pada Elips
Kriteria kedua adalah letak titik berada pada garis elips. Kedudukan titik pada elips akan terletak di dalam elips jika hasil hitung dari substitusi nilai titik ke persamaan elips menghasilkan nilai sama dengan satu. Lebih jelasnya perhatikan kriteria di bawah.

Contoh 2 soal menentukan kedudukan titik terhadap elips
Tentukan kedudukan titik (4, –3) pada elips dengan persamaan berikut!
Baca Juga: Kedudukan Garis Terhadap Elips
Penyelesaian:
Substitusi titik (4, –3) pada persamaan elips, sehingga akan diperoleh perhitungan sebagai berikut.
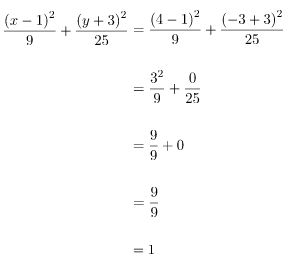
Diperoleh hasil perhitungannya adalah 1 (satu). Berdasarkan kriteria kedudukan titik terhadap elips, dan tanpa menggambarnya terlebih dahulu, akan diperoleh kesimpulan bahwa titik (4, –3) terletak pada elips.
Untuk melihat kebenarannya, perhatikan gambar elips dan letak titik sesuai pada soal yang diberikan.

Terlihat bahwa titik terletak pada elips, bukan?
Baca Juga: Irisan Kerucut Berupa Elips
Kedudupan Titik di Luar Elips
Berikutnya adalah kriteria kedudukan titik terhadap elips yang terakhir akan dibahas di sini, yaitu letak titik di luar elips. Kedudukan titik di luar elips akan terjadi jika hasil hitung dari substitusi nilai titik ke persamaan elips menghasilkan nilai lebih dari satu. Lebih jelasnya perhatikan kriteria di bawah.

Contoh 3 soal menentukan kedudukan titik terhadap elips
Soal:
Tentukan kedudukan titik (3, 6) pada elips dengan persamaan berikut!
Penyelesaian:
Substitusi titik (3, 6) pada persamaan elips, sehingga akan diperoleh perhitungan sebagai berikut.

Diperoleh hasil perhitungannya adalah 3154/225, nilainya lebih dari satu (> 1 ). Sehingga, tanpa menggambarnya terlebih dahulu, dapat disimpulkan bahwa titik (3, 6) terletak di luar elips. Untuk melihat kebenarannya, perhatikan gambar elips dan letak titik sesuai pada soal yang diberikan.
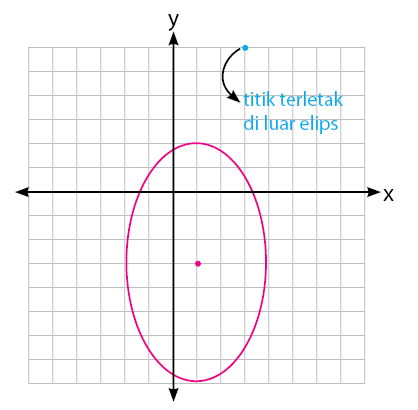
Terlihat bahwa titik terletak di luar elips.
Itu dia tiga kondisi yang dapat terjadi pada kedudukan titik terhadap elips. Kedudukan titik dapat diketahui melalui substitusi titik koordinat pada persamaan elips. Tanpa perlu menggambar elips dan titik terlebih dahulu.
Rangkuman kesimpulan dari tiga kriteria kedudukan titik terhadap elips dapat dilihat pada tabel di bawah.

Sekian pembahasan mengenai kedudukan titik terhadap elips. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Persamaan Garis Singgung Elips