Sebelum masuk pembahasan cara menentukan akar-akar persamaan polinomial, ingat kembali cara mencari akar-akar persamaan kuadrat. Persamaan kuadrat adalah persamaan polinomial berderajat 2 (memiliki pangkat tertinggi dua). Cara memperoleh akar-akar persamaan kuadrat dapat menggunakan rumus abc, pemfaktoran, atau melengkapkan kuadrat sempurna. Sayangnya, ketiga cara tersebut tidak dapat digunakan untuk menentukan akar akar persamaan polinomial berderajat tinggi, seperti pada polinomial berderajat 3, 4, dan seterusnya.
Lalu, bagaimana cara mencari akar-akar persamaan pangkat 3 atau pangkat yang lebih tinggi lainnya? Caranya adalah menggunakan cara horner. Cara horner atau biasa disebut dengan cara skema/bagan dapat digunakan untuk mencari akar-akar persamaan pangkat 3 (polinomial berderajat 3). Bahkan tidak hanya sebatas polinomial berderajat 3, tetapi juga untuk polinomial dengan derajat lebih tinggi.
Baca Juga: Toerema Sisa dan Teorema Faktor
Bagaimana cara menentukan akar akar persamaan polinomial? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Langkah pada Cara Mencari Akar Akar Persamaan Polinomial (Suku Banyak)
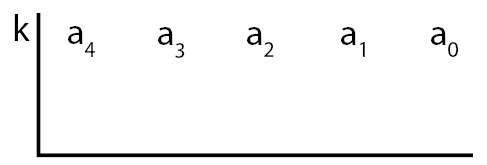
Pertama, pada pembahasan di bawah ini akan ditunjukkan proses mencari persamaan pangkat 3. Kunci dari cara horner adalah memilih bilangan k yang tepat. Bilangan k dipilih dengan cara menebak, trial and error, sehingga memperoleh hasil nol pada proses akhir.
Pemilihan bilangan yang tidak tepat mengakibatkan hasil akhir tidak bernilai nol (memiliki sisa). Awal mencoba cara horner, mungkin sobat idschool akan kesulitan menebak bilangan k, sehingga sobat idschool akan membutuhkan waktu untuk mencoba bilangan-bilangan yang cocok.
Namun jangan khawatir, seiring dengan banyak-banyak latihan, sobat idschool akan terasah kemampuannya dalam menebak bilangan k yang tepat, sehingga tidak perlu banyak mengalami error.
Sekarang perhatikan proses mencari akar-akar persamaan suku banyak berderajat 3 pada contoh soal di bawah.
Soal:
Tentukan akar akar persamaan polinomial f(x) = x3 ‒ 3x2 + 3x ‒ 1!
Pembahasan:
Langkah pertama adalah menentukan nilai bilangan k yang dapat menghasilkan bilangan 0 pada bagian akhir. Cobalah dari nilai yang paling kecil seperti k = 1.

Perhatikan bahwa proses akhirnya bernilai nol (tidak memiliki sisa), artinya tebakan kita untuk bilangan k = 1 tepat.
Selanjutnya, berdasarkan hasil bagan cara corner di atas dapat diperoleh persamaan di bawah.
f(x) = x3 ‒ 3x2 + 3x ‒ 1
f(x) = (x ‒ 1)(x2 ‒ 2x + 1)
Bentuk f(x) pada persamaan di atas memiliki pangkat tertinggi 2, artinya masih bisa difaktorkan lagi. Cara memfaktorkan persamaan kuadrat tidak perlu menggunakan cara horner, walaupun cara horner tetap bisa digunakan.
Namun, bagi yang sudah menguasai cara melakukan pemfaktoran dengan cara biasa, pastinya akan lebih cepat. Jadi, sebaiknya sobat idschool tidak melupakan materi-materi sebelumnya. Sekarang mari kita faktorkan persamaan kuadrat yang terdapat pada persamaan f(x).
Persamaan kuadrat yang akan difaktorkan: x2 ‒ 2x + 1
Jika akar-akar persamaan kuadrat tersebut adalah x1 dan x2 maka cari kedua bilangan yang memenuhi syarat berikut.
x1 + x2 = ‒(‒2)/1 = 2
x1 ∙ x2 = 1/1 = 1
Dua bilangan yang memenuhi kedua syarat tersebut adalah 1, sehingga faktor persamaan kuadrat x2 ‒ 2x + 1 adalah x2 ‒ 2x + 1 = (x ‒ 1)(x ‒ 1).
Bagi yang belum paham cara di atas bisa dilihat kembali bagaimana cara memfaktorkan persamaan kuadrat.
Sehingga, kita peroleh persamaan f(x) menjadi persamaan seperti bentuk berikut.
x3 ‒ 3x2 + 3x ‒ 1 = (x ‒ 1)(x ‒ 1)(x ‒ 1)
x3 ‒ 3x2 + 3x ‒ 1 = ( x ‒ 1)3
Jadi, faktor-faktor persamaan dari f(x) = x3 ‒ 3x2 + 3x ‒ 1 adalah ( x ‒ 1) adalah x – 1, di mana akar akar persamaan polinomial mempunyai 3 akar kembar yaitu x = 1.
Bagaimana? Mudah bukan? Begitulah cara menentukan akar- akar Persamaan Polinomial. Pada pembahasan ini diberikan contoh soal dan pembahasan dalam mencari akar-akar persamaan pangkat 3. Langkah menyelesaikan persamaan untuk derajat yang lebih tinggi sama dengan proses ini.
Jika masih ada pertanyaan bisa tinggalkan komentar pada kolom di bawah. Jika ada bagian yang mungkin kurang teliti dalam menghitung bisa juga tinggalkan komentar pada kolom di bawah. Terimakasih sudah berkunjung di idschool.net, semoga bermanfaat.
Baca Juga: Contoh Soal Jumlah dan Hasil Kali Akar-akar Polinomial

adakah cara selain menebak untuk menentukan nilai bilangan k yang dapat menghasilkan bilangan 0 pada bagian akhir?