Contoh Soal dan Pembahasan Program Linear Matematika SMA

Program linear merupakan bahasan materi tentang optimasi yang pada umumnya berkaitan dengan bagaimana cara memaksimalkan untung atau meminimalkan biaya produksi. Tujuannya sangat jelas, untuk mendapatkan perhitungan dan perencanaan yang tepat untuk suatu kegiatan produksi. Bahasan materi program linear Matematika SMA antara lain meliputi sistem pertidaksamaan linear, model matematika, dan metode untuk menyelesaikan masalah terkait program linear.

Bagaimana bentuk soal dan pembahasan program linear Matematika SMA? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Sistem Pertidaksamaan Linear
• Model Matematika
  • Contoh pemodelan soal cerita program linear matematika
• Cara Menyelesaikan Masalah Program Linear Matematika
  • Metode Uji Titik Pojok
  • Metode Garis Selidik
• Contoh Soal dan Pembahasan
  • Contoh 1: Soal Program Linear
  • Contoh 2: Soal Program Linear Matematika

Sistem Pertidaksamaan Linear

Pertidaksamaan linear merupakan sebuah pertidaksamaan dengan kombinasi operasi antar variabel yang ditandai dengan tanda < (kurang dari), ≤ (kurang dari sama dengan), > (lebih dari), atau ≥ (lebih dari sama dengan). Sedangkan gabungan dari beberapa pertidaksamaan linear disebut sistem pertidaksamaan linear.

Sistem pertidaksamaan linear pada program linear Matematika SMA biasanya melibatkan dua variabel dengan dua atau lebih pertidaksamaan linear. Beberapa pertidaksamaan dalam sistem pertidaksamaan merupakan fungsi kendala yang memuat himpunan penyelesaian.

Salah satu langkah dalam menyelesaikan sistem pertidaksamaan linear matematika sebagai fungsi kendala adalah menggambarkan garis dan daerah layak yang memenuhi pada bidang kartesius.

Berikut ini adalah langkah-lakah untuk membuat garis lurus dan menentukan daerah yang memenuhi:

1. Gambarlah garis ax + by = c pada bidang kartesius, cara lebih lengkapnya dapat dilihat di sini.

2. Ambil sembarang titik (x₁, y₁) di luar garis ax + by = c kemudian hitung nilai ax₁ + by₁ dan bandingkan dengan nilai pada ruas kanan pertidaksamaan (nilai c).

3. Jika nilai ax₁ + by₁ ≤ c maka daerah yang memuat titik (x₁, y₁) adalah daerah penyelesaian berada di bawah garis ax + by = c.

4. Jika ax₁ + by₁ ≥ c maka daerah yang memuat titik (x₁, y₁) adalah daerah penyelesaian berada di atas pertidaksamaan ax + by = c.

Pada bagian ini, sobat akan mempelajari bagaimana cara menggambarkan garis kendala dan menentukan daerah layak yang memenuhi melalui penyelesaian contoh berikut,

Sistem pertidaksamaan linear:
x ≥ 0
y ≥ 0
x + y ≤ 7
x + 3y ≤ 15

Cari tahu daerah yang memenuhi sistem pertidaksamaan linear di atas melalui beberapa langkah penyelesaian masalah program linear matematika di bawah.

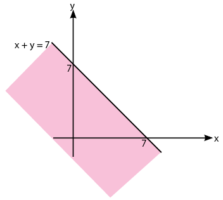
1. Daerah yang memenuhi pertidaksamaan x + y ≤ 7.

2. Daerah yang memenuhi pertidaksamaan x + 3y ≤ 15.

3. Menentukan daerah yang memenuhi gabungan dari empat sistem pertidaksamaan linear: x ≥ 0, y ≥ 0, x + y ≤ 7, dan x + 3y ≤ 15.

Baca Juga: Persamaan dan Pertidaksamaan Linear Satu Variabel

Model Matematika

Model soal yang diberikan pada program linear matematika biasanya berupa soal cerita. Agar dapat menyelesaikan soal cerita yang diberikan, sobat idschool perlu merubahnya ke dalam model matematika. Model matematika pada soal program linear matematika merupakan suatu cara merubah permasalahan sehari-hari ke dalam bentuk persamaan/pertidaksamaan.

Untuk penjelasan lebih detailnya, sobat idschool dapat mencari tahu bagaimana cara mendapatkan pemodelan soal program linear matematika pada penyelesaian kasus berikut.

Contoh pemodelan soal cerita program linear matematika

Contoh 1: Tentukan model matematika dari soal di bawah.
Sebuah adonan roti basah dibuat dengan 2 kg tepung dan 2 kg gula. Sedangkan sebuah adonan roti kering dibuat menggunakan 1 kg tepung dan 2 kg gula. Ibu memiliki persediaan tepung sebanyak 6 kg dan gula sebanyak 10 kg. Setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00.

Berapakah banyak kombinasi adonan roti yang dapat dibuat untuk mendapatkan keuntungan maksimal?

Pembahasan:
Kita akan membuat model dari soal cerita program linear matematika di atas dengan pemisalan x = adonan roti basah dan y = adonan roti kering.

Secara ringkas, kebutuhan untuk membuat roti basah (x) dan roti kering diberikan seperti tabel di bawah.

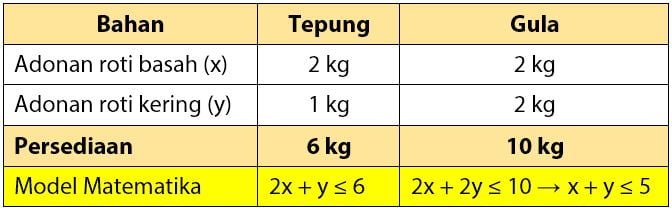
Dari tabel di atas dapat diperoleh model matematika dalam sebuah sistem pertidaksamaan matematika sebagai berikut.

• x ≥ 0
• y ≥ 0
• 2x + y ≤ 6
• x + y ≤ 5

Pembahasan yang diberikan sampai sini belum bisa menentukan kombinasi jenis roti yang dibuat untuk mendapatkan keuntungan maksimal. Solusi selanjutnya akan dibahas pada penjabaran menyelesaikan masalah program linear matematika sma di bawah.

Baca Juga: Sistem Persamaan Linear Dua Variabel

Cara Menyelesaikan Masalah Program Linear Matematika

Cara menyelesaikan masalah program linear matematika dapat dikatakan sebagai proses untuk menentukan nilai optimum dari suatu pertidaksamaan. Nilai tersebut dapat berupa nilai maksimum atau minimum, tergantung dari soal yang diberikan. Bentuk umum fungsi objektif dari suatu model matematika adalah f(x,y) = ax + by.

Terdapat dua metode yang dapat digunakan untuk menentukan nilai optimum tersebut yaitu metode uji titik pojok dan garis selidik. Penjabaran secara lebih jelasnya dapat dilihat pada pembahasan di bawah.

Metode Uji Titik Pojok

Sesuai namanya, metode uji titik pojok dilakukan dengan menghitung nilai fungsi tujuan dari titik pojok yang diperoleh. Titik pojok yang dimaksud di sini adalah titik-titik koordinat yang membatasi daerah layak dari suatu sistem pertidaksamaan linear.

Langkah-langkah yang dilakukan untuk menentukan nilai optimum dengan metode uji titik pojok adalah sebagai berikut.

1. Menentukan garis-garis sistem pertidaksamaan yang menjadi fungsi kendala dari persoalan yang diberikan.
2. Menentukan titik-titik pojok yang merupakan koordinat pembatas daerah yang memenuhi fungsi kendala.
3. Menghitung nilai optimum f(x,y) dari titik-titik pojok yang diperoleh.
4. Mendapatkan nilai maksimum atau minimum sesuai permasalahan.

Untuk memperjelas pemahaman materi tentang mencari nilai optimum dengan metode uji titik pojok, kita akan menyelesaikan permasalah yang telah dibahas sebagian pada bagian model matematika.

Lihat kembali soal yang diberikan, fungsi tujuan dapat diperoleh dari kalimat: Jika setiap satu adonan kue basah dapat memberikan untung Rp75.000,00 dan setiap adonan kue kering dapat memberikan untung Rp60.000,00.

Jadi, fungsi tujuannya adalah memaksimalkan f(x, y) = 75.000x + 60.000y.

Berdasarkan pembahasan sebelumnya diperoleh sistem pertidaksamaan berikut.

• x ≥ 0
• y ≥ 0
• 2x + y ≤ 6
• x + y ≤ 5

Menggambar daerah yang memenuhi sistem pertidaksamaan di atas.

Menentukan titik koordinat yang mennjadi titik pojok pembatas daerah layak dari permasalahan sistem pertidaksamaan.

Titik Koordinat O, A, dan C dapat diperoleh dengan melihat gambar di atas, yaitu O(0,0), A(0, 5), dan C(3, 0). Sedangkan koordinat titik B dapat diperoleh dengan menggunakan metode eliminasi.

Mencari koordinat titik B.

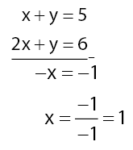
Substitusi nilai x = 1 pada persamaan x + y = 5 untuk mendapatkan nilai y.
x + y = 5
1 + y = 5
y = 5 – 1 = 4

Diperoleh koordinat titik B adalah (1, 4)

Perhitungan nilai optimum dari penyelesian soal cerita program linear matematika seperti berikut.

Jadi, nilai keuntungan maksimum yang dapat diperoleh adalah Rp315.000,00 dengan membuat 1 (satu) adonan roti basah dan 4 (empat) adonan roti kering.

Baca Juga: Sistem Persamaan Linear Tiga Variabel (SPLTV)

Metode Garis Selidik

Selain metode uji titik pojok, cara lain yang dapat digunakan untuk mengetahui nilai optimum adalah metode garis selidik. Intinya, cara yang dapat dilakukan untuk mencari nilai optimum dengan garis selidik yang diperoleh dari persamaan fungsi objektif atau fungsi tujuannya.

Jika fungsi tujuan adalah memaksimalkan maka nilai optimum diperoleh dari titik yang paling akhir menyentuh garis selidik yang digeser ke kanan mendekati daerah layak. Sedangkan nilai optimum dengan fungsi tujuan meminimumkan diperoleh dari titik koordinat yang pertama kali menyentuh geseran garis selidik yang digeser ke kiri mendekati daerah layak. Begitu juga dengan sebaliknya.

Berikut ini adalah langkah-langkah menentukan nilai optimum fungsi objektif f(x,y) = ax + by dengan metode garis selidik.

1. Menentukan daerah yang memenuhi sistem pertidaksamaan yang diberikan.
2. Menentukan persamaan garis selidik f(x,y) = ax + by = k, dengan k adalah bilangan real.
3. Geser garis selidik yang telah dibuat pada langkah nomor 2 atau buatlah garis-garis lain yang sejajar dengan garis selidik yang telah dibuat ke arah daerah layak.
4. Jika titik (x₁, y₁) adalah titik pada daerah penyelesaian yang pertama dilalui oleh garis selidik maka nilai minimum diwakili oleh titik tersebut.
5. Jika titik (x₂, y₂) adalah titik pada daerah penyelesaian yang terakhir dilalui oleh garis selidik maka nilai maksimum diwakili oleh titik tersebut.

Untuk memperjelas pemahaman materi tentang mencari nilai optimum dengan metode garis selidik, kita akan menggunakannya untuk menyelesaikan permasalah yang telah dibahas sebagian pada bagian model matematika.

Berdasarkan pembahasan sebelumnya diperoleh sistem pertidaksamaan berikut.

• x ≥ 0
• y ≥ 0
• 2x + y ≤ 6
• x + y ≤ 5

Fungsi tujuan: memaksimalkan f(x, y) = 75.000x + 60.000y.

Persamaan garis selidik (ambil nilai k = 600.000, nilai k diambil sembarang):
f(x, y) = k
75.000x + 60.000y = 600.000
5x + 4y = 40

Menggambar daerah yang memenuhi sistem pertidaksamaan di atas dan garis selidiknya.

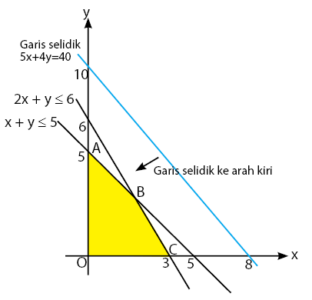
Nilai maksimum diwakili oleh titik B (titik yang pertama kali menyentuh garis selidik yang digeser ke arah kiri).

Mencari koordinat titik B.

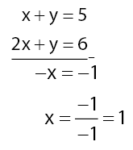
Substitusi nilai x = 1 pada persamaan x + y = 5 untuk mendapatkan nilai y.

x + y = 5
1 + y = 5
y = 5 – 1 = 4

Koordinat titik B adalah (1, 4), selanjutnya substitusi koordinat titik B pada persamaan f(x, y) = 75.000x + 60.000y:f(x, y) = 75.000x + 60.000y
f(x, y) = 75.000(1) + 60.000(4)
f(x, y) = 75.000 + 240.000
f(x, y) = 315.000

Jadi, nilai keuntungan maksimum yang dapat diperoleh adalah Rp315.000,00 dengan membuat 1 (satu) adonan roti basah dan 4 (empat) adonan roti kering.

Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear (SPL) dengan Matriks

Dua cara menghasilkan hasil yang sama, bukan? Untuk selanjutnya sobat idschool bisa pilih salah satu caranya. Pilih satu cara yang menurut sobat idschool paling mudah.

Contoh Soal dan Pembahasan

Bagian terakhir yaitu mengenai contoh soal dan pembahasan program linear matematika sma yang akan diberikan dalam contoh-contoh soal berikut. Setiap contoh soal yang diberikan dilengkapi dengan pembahasan soal program linear matematika sma. Sobat idschool dapat menggunakan pembahasan program linear matematika tersebut sebagai tolak ukur keberhasilan mengerjakan soal.

Contoh 1: Soal Program Linear

Luas daerah parkir 360 m². Luas rata-rata sebuah mobil 6 m² dan luas rata – rata bus 24 m². Daerah parkir tersebut dapat memuat paling banyak 30 kendaraan roda empat (mobil dan bus). Jika tarif parkir mobil Rp2.000,00 dan tarif parkir bus Rp5.000,00 maka pendapatan terbesar yang dapat diperoleh adalah ….
A. Rp40.000,00
B. Rp50.000,00
C. Rp60.000,00
D. Rp75.000,00
E. Rp90.000,00

Pembahasan:
Misalkan x = banyak mobil dan y = banyak bus, maka soal cerita prgoram linear matematika dapat diringkas seperti tabel di bawah.

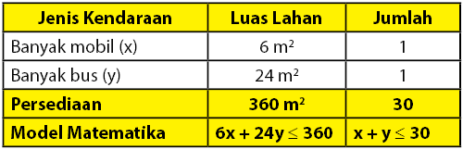
Diperoleh dua persamaan: (i) x + y ≤ 30 dan (ii) 6x + 24y ≤ 360 → x + 4y ≤ 60, dari keduanya dapat ditentukan daerah layak yang memenuhi pertidaksamaan seperti berikut.

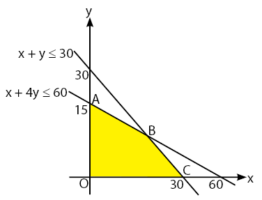
Titik koordinat O, A, dan C dapat diperoleh dengan melihat gambar, yaitu O(0,0), A(0, 15), dan C(30,0). Untuk koordinat B dapat diperoleh dengan menggunakan eliminasi dan substitusi.

Substitusi nilai y = 10 pada persamaan x + y = 30 untuk mendapatkan nilai x.
x + y = 30
x + 10 = 30
x = 30 – 10 = 20
Sehingga diperoleh koordinat titik B adalah (20, 10)

Perhitungan keuntungan maksimal yang dapat diperoleh:

Jadi, pendapatan terbesar yang dapat diperoleh adalah Rp90.000,00

Jawaban: E

Baca Juga: Pertidaksamaan Kuadrat dan Himpunan Penyelesaiannya

Contoh 2: Soal Program Linear Matematika

Biaya produksi satu buah payung jenis A adalah Rp20.000,00 per buah, sedangkan biaya satu buah produksi payung jenis B adalah Rp30.000,00. Seorang pengusaha akan membuat payung A dengan jumlah tidak kurang dari 40 buah. Sedangkan banyaknya payung jenis B yang akan diproduksi minimal adalah dari 50 buah. Jumlah maksimal produksi kedua payung tersebut adalah 100 buah. Biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai ketentuan tersebut adalah ….
A.     Rp2.000.000,00
B.     Rp2.300.000,00
C.     Rp2.200.000,00
D.     Rp2.100.000,00
E.     Rp2.000.000,00

Pembahasan:
Misalkan x = banyak payung A dan y = banyak payung B, model matematika dari permasalahan tersebut memenuhi fungs-fungsi berikut,

Fungsi tujuan: meminimumkan f(x,y) = 20.000x + 30.000y
Fungsi kendala:
x ≥ 40
y ≥ 50
x + y ≤ 100

Daerah penyelesaian yang memenuhi permasalahan soal cerita program linear matematika pada soal.

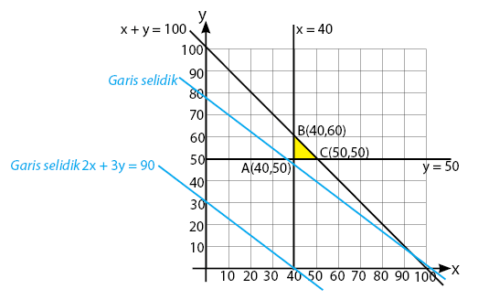
Nilai minimum akan diperoleh melalui titik koordinat yang dilalui garis selidik yang pertama kali, yaitu titik A(40, 50).

Menghitung biaya produksi minimum:
f(40,50) = 20.000(40) + 30.000(50)
f(40,50) = 800.000 + 1.500.000
f(40,50) = 2.300.000

Jadi, biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai ketentuan tersebut adalah Rp2.300.000,00.

Jawaban: B

Oke, sekian dulu pembahasan mengenai contoh soal program linear matematika dan pembahasannya. Semoga bermanfaat, terimakasih telah berkunjung di idschool(dot)net.

Baca Juga: Cara Mencari Luas Daerah yang Dibatasi Kurva