Jarak Dua Garis Bersilangan pada Kubus +Rumus Cepatnya

Jarak dua garis bersilangan sama dengan jarak terpendek antara 2 bidang yang masing-masing memuat garis. Atau jarak dua garis bersilangan sama dengan jarak salah satu titik pada garis dan proyeksi titik tersebut pada bidang yang memuat garis lain. Pengertian tersebut sangat dibutuhkan untuk menentukan jarak dua garis bersilangan pada kubus.

Cara menghitung jarak dua garis bersilangan bergantung dari informasi apa yang diketahui. Namun, jarak dua garis bersilangan selalu merupakan jarak titik pada suatu garis ke proyeksi tersebut ke bidang yang memuat titik lainnya. Bagaimana cara menghitung jarak dua garis bersilangan pada kubus ABCD.EFGH? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Daftar isi:

• Pengertian Dua Garis Bersilangan pada Kubus ABCDEFGH
• Jarak Dua Garis Bersilangan
• Contoh Soal dan Pembahasan
  • Contoh 1 – Jarak BG dan CE adalah …
  • Contoh 2 – Jarak garis AB dan DF pada kubus ABCD.EFGH dengan panjang rusuk 4 cm adalah .…

Pengertian Dua Garis Bersilangan pada Kubus ABCDEFGH

Dua buah garis dikatakan sebagai pasangan garis bersilangan jika tidak memiliki titik potong (jika diperpanjang) dan tidak sejajar.

Ada cukup banyak pasangan garis bersilangan pada kubus ABCDEFGH. Pasangan garis bersilangan biasanya terletak pada bidang datar yang berbeda. Dua garis bersilangan akan memiliki titik potong jika salah satu garis digeser menuju garis lain. Gambar berikut menunjukkan beberapa contoh pasangan garis bersilangan pada kubus ABCDEFGH.

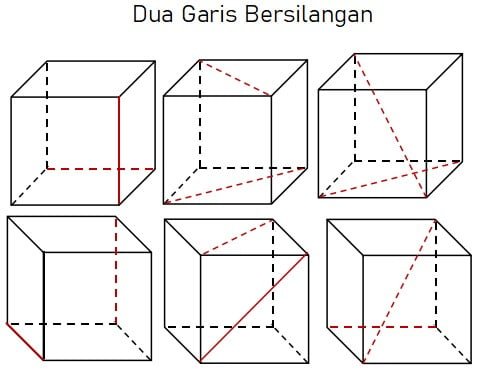
Baca Juga: Ringkasan Materi dan Kumpulan Rumus Dimensi Tiga

Jarak Dua Garis Bersilangan

Cara menghitung jarak dua garis bersilangan dapat dilakukan melalui beberapa langkah. Misalnya, diketahui kedudukan garis g bersilangan dengan garis h yang keduanya terletak pada bidang datar berbeda. Jarak dua garis tersebut sama dengan panjang segmen garis yang dihasilkan melalui langkah-langkah berikut.

Langkah-langkah menghitung jarak antara dua garis bersilangan:

1. Membuat bidang α yang memuat garis h dan sejajar garis g
2. Ambil sembarang titik A pada garis g dan proyeksikan titik A ke bidang α
3. Jika hasil proyeksi pada bidang α adalah titik A’ maka jarak garis g yang bersilangan dengan garis h adalah panjang garis proyektor AA’.

Semua panjang rusuk pada kubus ABCD.EFGH adalah sama dan sisi kubus berpotongan saling tegak lurus. Kondisi tersebut membuat jarak dua garis bersilangan pada kubus ABCDEFGH dapat diketahui melalui beberapa langkah perhitungan.

Sebagai contoh sederhana, perhatikan cara mengetahui jarak dua garis bersilangan pada kubus ABCDEFGH berikut.

Soal:
Kubus ABCD.EFGH memiliki panjang rusuk sama dengan 6 cm. Hitung jarak antara garis AH dan BF!

Penyelesaian:
Kedudukan garis AH dan BF pada kubus ABCDEFGH adalah saling bersilangan. Garis AH terletak pada bidang ACHE, sedangkan garis BF terletak pada bidang BCGF.

Garis AH sejajar dengan bidang BCGF, sehingga setiap proyeksi titik dari garis AH ke bidang BCGF sama dengan jarak garis AH ke garis BF.

Jarak setiap titik pada garis AH ke bidang BCGF sama dengan panjang rusuk kubus. Jadi, dapat disimpulkan bahwa jarak garis AH ke garis BF sama dengan panjang rusuk kubus yaitu 6 cm.

Baca Juga: Cara Menentukan Kedudukan Antara Dua Lingkaran

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool dapat gunakan untuk menambah pemahaman bahasan jarak dua garis bersilangan pada kubus. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya.

Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Jarak BG dan CE adalah …

Sebuah kubus ABCD.EFGH memiliki panjang rusuk 12 cm. Jarak BG dan CE adalah … cm
A. 2√3
B. 2√5
C. 2√6
D. 3√2
E. 3√3

Pembahasan:
Pasangan garis BG dan CE merupakan dua garis bersilangan. Bidang yang memuat CE adalah bidang diagonal ACGE. Ambil titik T pada garis BG dan proyeksikan ke bidang ACGE. Misalkan titik hasil proyeksi adalah T’, jarak garis BG dan CE sama dengan panjang ruas garis ACGE.

• Keterangan perhitungan panjang ruas garis:
  • CE = diagonal ruang = 12√3 cm
  • BC = diagonal sisi = 12√2 cm
  • TC = ¹/₂ × diagonal sisi = ¹/₂ × 12√2 = 6√2 cm

Jarak garis BG ke garis CE = panjang ruas garis TT’ yang dapat diketahui menggunakan persamaan panjang TT’ dari segitiga ETT’ dan TT’ dari segitiga CTT’ seperti penyelesaian berikut.

Mencari nilai x:

(6√2)² – (12√3 – x)² = (6√2)² – x²

72 – (432 – 24√3x + x²) = 216 – x²

72 – 432 + 24√3x – x² = 216 – x²

24√3x = 576

Setelah mendapat panjang T’E = x = 8√3 cm selanjutnya dapat dihitung panjang TT’ yang merupakan jarak garis BG ke garis CE.

Menghitung panjang ruas garis TT’:

TT’² = TE² − T’E² = (6√6)² − (8√3)²

TT’² = 216 − 192 = 24

Sehingga,

TT’ = √24 = √(4×6) = 2√6 cm

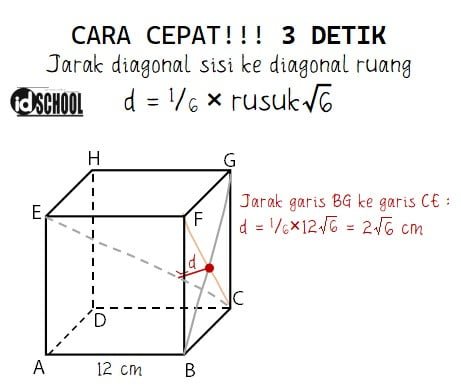
Jadi, jarak BG dan CE sama dengan 2√6 cm.

Jawaban: C

Baca Juga: Rumus Transformasi Geometri (Translasi. Refleksi, Rotasi, dan Dilatasi)

Contoh 2 – Jarak garis AB dan DF pada kubus ABCD.EFGH dengan panjang rusuk 4 cm adalah .…

Jarak garis AB dan DF pada kubus ABCD.EFGH dengan panjang rusuk 4 cm adalah .…
A. 3√3 cm
B. 3√2 cm
C. 2√3 cm
D. 2√2 cm
E. √3 cm

Pembahasan:
Misalkan titik P adalah titik tengah AB maka AP = PB = 2 cm dan proyeksi titik P pada garis PF adalah titik Q. Jarak garis AB ke garis DF sama dengan panjang segmen garis PQ. Di mana Q adalah titik tengah garis FD sehingga DQ = QF = ¹/₂ × diagonal ruang = ¹/₂ × 4√3 = 2√3 cm.

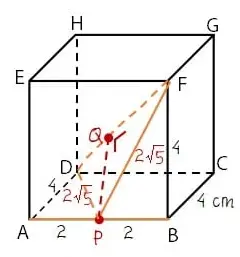
Cara menghitung panjang garis PF:

PF² = PB² + BF² = 2² + 4²

PF² = 4 + 16 = 20

Sehingga,

PF = √(4×5) = √4 × √5 = 2√5 cm

Cara menghitung panjang garis PQ:

PQ² = PF² – QF² = 20 + (2√3)²

PF² = 20 – 12 = 8

PF = √(4×2) = √4 × √2 = 2√2 cm

Jadi, jarak garis AB dan DF pada kubus ABCD.EFGH sama dengan PQ = 2√2 cm.

Jawaban: D

Demikianlah tadi ulasan cara menghitung jarak dua garis bersilangan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Materi Pengantar Dimensi Tiga