Ragam atau Variansi merupakan salah satu ukuran penyebaran data. Nilanya menunjukkan bagaimana penyebaran data terhadap rata-rata. Rumus variansi dibedakan menjadi dua yaitu untuk data sampel dan populasi. Rumusnya adalah rata-rata selisih kuadrat data dengan rata-rata data.
Cara menggunakan rumus variansi akan dijelaskan melalui ulasan di bawah.
Daftar isi:
Baca Juga: Ukuran Penyebaran Data
Rumus Variansi
Nilai variansi digunakan pada pengujian hipotesis, pengecekan goodness of fit, dan pengambilan sampel Monte Carlo. Variansi untuk data populasi disimbolkan σ2. Sementara simbol variansi untuk data sampel disimbolkan s2. Sehingga ada dua rumus variansi berdasar jenis data yang digunakan.
Penyajian data dapat berupa data tunggal dan kelompok. Untuk setiap penyajian data dapat menggunakan data pupulasi atau data sampel. Sehingga ada empat rumus variansi yang perlu diketahui.
Rumus variansi meliputi empat persamaan berikut.

Keterangan:
σ2 = variansi
i = bilangan asli: 1, 2, 3, …, N
xi = data ke – i
Me = mean (rata-rata)
N = banyak data
fi = frekuensi
Baca Juga: Rumus Mean, Median, dan Modus Data Kelompok
Cara Menghitung Variansi
Dalam menggunakan rumus variansi perlu memerhatikan data yang dimiliki. Apakah data sampel atau populasi. Cara menghitung variansi untuk penyajian data tunggal dan kelompok ada di bawah.
1) Data tunggal
Soal 1:
Carilah nilai variansi dari sampel data tunggal 2, 5, 9, 11, dan 13!
Penyelesaian:
Data tunggal yang ada merupakan data sampel. Sehingga rumus yang digunakan adalah s2 = Σ(xi – x̅)2/(N – 1).
1) Menghitung rata-rata (x̅):
2) Kuadrat selisih setiap data dengan rata-rata:
| xi | xi – x̅ | (xi – x̅)2 |
| 2 | –6 | 36 |
| 5 | –3 | 9 |
| 9 | 1 | 1 |
| 11 | 3 | 9 |
| 13 | 5 | 25 |
3) Menghitung variansi data sampel (s2):
2) Data kelompok
Soal 2:
Perhatikan tabel berikut!
| Nilai | Frekuensi |
| 50 – 59 | 7 |
| 60 – 69 | 10 |
| 70 – 79 | 15 |
| 80 – 89 | 12 |
| 90 – 99 | 6 |
Tentukan nilai variansi dari populasi data di atas!
Jawab:
Data kelompok pada tabel yang diberikan merupakan data populasi. Sehingga rumus variansi yang digunakan adalah σ2 = Σfi·(xi – x̅)2/N.
1) Menghitung rata-rata data kelompok:
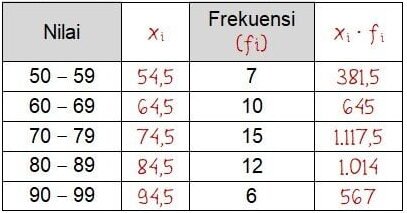
Rata-rata:
2) Hasil kali frekuensi dengan kuadrat selisih setiap data dengan rata-rata:
| xi | fi | xi – x̅ | (xi – x̅)2 | fi×(xi – x̅)2 |
| 54,5 | 7 | –20 | 400 | 2.800 |
| 64,5 | 10 | –10 | 100 | 1.000 |
| 74,5 | 15 | 0 | 0 | 0 |
| 84,5 | 12 | 10 | 100 | 1.200 |
| 94,5 | 6 | 20 | 400 | 2.400 |
3) Menghitung variansi:
Jadi, variansi dari populasi data pada tabel adalah 148.
Baca Juga: Rumus Desil dan Persentil Data Kelompok
Interpretasi Nilai Variansi
Nilai variansi menunjukkan penyebaran data di sekitar mean. Saat nilai variansi kecil, titik-titik data berada dekat dengan rata-rata. Sementara saat nilai variansi besar (tinggi), titik-titik data terletak menyebar jauh dari rata-rata.
Perhatikan bagaimana penyeberan titik-titik data dan nilai variansi data berikut.
Saat nilai variansi sama dengan nol (σ2 = 0), data yang digunakan berupa nilai-nilai identik (sama).
Baca Juga: Median Data Kelompok
Contoh Soal dan Pembahasan
Latihan soal menghitung variansi dan pembahasannya ada di bawah.
Contoh 1 – Penggunaan Rumus Variansi
Variansi dari data 8, 9, 10, 11, 12, 12, 12, dan 14 adalah ….
A. 3,25
B. 3
C. 2,25
D. 2
E. 1
Pembahasan:
Perta perlu untuk hitung rata-rata terlebih dahulu.
Menghitung rata-rata (x̅):
Menghitung selisih kuadrat dari setiap data:
| xi | xi – x̅ | (xi – x̅)2 |
| 8 | –3 | 9 |
| 9 | –2 | 4 |
| 10 | –1 | 1 |
| 11 | 0 | 0 |
| 12 | 1 | 1 |
| 12 | 1 | 1 |
| 12 | 1 | 1 |
| 14 | 3 | 9 |
Menghitung variansi:
Jadi, variansi dari data 8, 9, 10, 11, 12, 12, 12, dan 14 adalah 3,25.
Jawaban: A
Baca Juga: Penyajian Poligon Data Kelompok
Contoh 2 – Penggunaan Rumus Variansi
Diketahui data tunggal dari suatu populasi: 8, 2, 10, x, dan 7. Jika rataannya 6 maka variansi dari data populasi tersebut adalah ….
A. 7,2
B. 8,2
C. 9,2
D. 10,2
E. 11,2
Pembahasan:
Langkah pertama, cari nilai x terlebih dahulu.
6 × 5 = 27 + x
30 = 27 + x
x = 30 – 27 = 3
Mencari kuadrat selisih setiap data dengan rata-ratanya:
| xi | xi – x̅ | (xi – x̅)2 |
| 8 | 2 | 4 |
| 2 | ‒4 | 16 |
| 10 | 4 | 16 |
| 3 | ‒3 | 9 |
| 7 | 1 | 1 |
Menghitung variansi data tunggal:
Jadi, variansi dari data populasi tersebut adalah 9,2.
Jawaban: C
Contoh 3 – Penggunaan Rumus Variansi
Perhatikan gambar berikut!

Variansi dari data nilai ulangan sejumlah siswa seperti yang diberikan pada histogram di atas adalah ….
A. 5,6
B. 50,6
C. 56
D. 50,56
E. 56,50
Pembahasan:
Dari penyajian data histogram dapat dicari nilai rata-rata data kelompok seperti berikut.
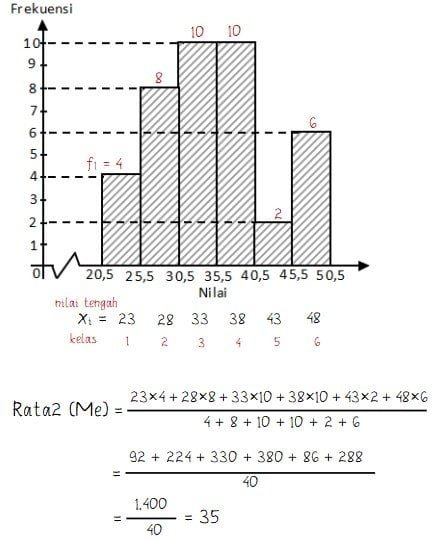
2) Menghitung kuadarat selisih setiap data dengan rata-rata:
| xi | fi | xi – x̅ | (xi – x̅)2 | fi·(xi – x̅)2 |
| 23 | 4 | –12 | 144 | 576 |
| 28 | 8 | –7 | 49 | 392 |
| 33 | 10 | –2 | 4 | 40 |
| 38 | 10 | 3 | 9 | 90 |
| 43 | 2 | 8 | 64 | 128 |
| 48 | 6 | 13 | 169 | 1.014 |
3) Menghitung variansi:
Jadi, variansi dari data nilai ulangan sejumlah siswa yang sesuai dengan histogram sama dengan σ2 = 56.
Jawaban: C
Demikianlah tadi ulasan rumus varians (ragam) beserta contoh cara menghitungnya dan bagaimana interpretasi nilai variansi. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!


