Himpunan dan diagram venn memiliki keterkaitan yang antara keduanya dalam bentuk visual. Himpunan menyatakan anggota yang dapat terdiri dari bilangan, huruf, atau kumpulan nama-nama yang memenuhi syarat tertentu. Sedangnkan diagram venn menggambarkan himpunan tersebut dalam sebuah diagram agar lebih mudah dipahami. Antara himpunan dan diagram venn dapat dikatakan sebagai data dan bentuk penyajian datanya. Di mana data dinyatakan dalam bentuk himpunan dan penyajian data berupa diagram venn.
Sebagai contoh sederhana, terdapat dua himpunan A dan himpunan B. Anggota himpunan A adalah bilangan ganjil < 15, sehingga dapat dituliskan A = {1, 3, 5, 7, 9, 11, 13}. Sedangkan himpunan B adalah himpunan bilangan kelipatan tiga yang kurang dari 17, atau dapat dituliskan dengan B = {3, 6, 9, 12, 15}. Perhathikan bahwa ada anggota himpunan A dan himpunan B yang sama. Hubungan himpunan dan diagram venn dari kedua himpunan tersebur sesuai dengan bentuk diagram venn berikut.
Baca Juga: Pengetian dan Contoh Kalimat Terbuka dan Kalimat Tertutup pada Matematika
Bagaiaman cara membentuk himpunan ke dalam bentuk diagram venn? Sobat idschool dapat mendari tahu jawabannya melalui ulasan himpunan dan diagram venn di bawah.
Table of Contents
- Cara Menyatakan Himpunan
- 3 Macam Himpunan
- Hubungan Antar Himpunan
- Sifat-Sifat Operasi Himpunan
- Contoh Soal dan Pembahasan
Cara Menyatakan Himpunan
Himpunan merupakan kumpulan benda atau objek yang didefinisikan dengan jelas. Lambang untuk menyimbolkan himpunan adalah huruf besar, misal A, B, C, dan lain sebagainya. Untuk menyatakan anggota dari sebuah himpunan adalah ∊. Sedangkan untuk menyatakan anggota yang tidak termasuk dalam sebuah himpunan adalah ∉.
Untuk menyatakan banyaknya anggota suatu himpunan A dinotasikan dengan n(A). Sebagai contoh pada anggota himpunan A = {1, 2, 3, 4, 5, 6, 7, 8, 9} memiliki banyak anggota himpunan A sebanyak 9 bilangan. Sehingga banyak anggota himpunan A dapat dituliskan dengan n(A) = 9
Suatu himpunan dapat memiliki anggota yang terhingga atau tak terhingga. Himpunan terhingga adalah himpunan dengan banyak anggota terhingga atau dibatasi sampai batas tertentu. Sedangkan, himpunan tak terhingga adalah himpunan dengan banyak anggota tak terbatas adalah himpunan tak berhingga.
Contoh:
Himpunan berhingga: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Himpunan tak berhingga: {25, 27, 29, 31, …}
Himpunan dapat dinyatakan dengan menyebutkan semua anggota, menuliskan sifat anggota, atau melalui notasi pembentuk himpunan. Contoh cara menyatakan himpunan diberikan seperti tiga cara berikut.
Contoh menyatakan himpunan dengan menyebutkan semua anggota:
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {25, 27, 29, 31, …}
Menuliskan sifat anggota:
A = himpunan bilangan asli kurang dari 10
B = himpunan bilangan ganjil lebih dari 23
Notasi pembentuk himpunan:
A = {x | x < 10, x ∊ bilangan asli}
G = {x | x > 23, x ∊ bilangan ganjil}
Baca Juga: Daerah Asal (Domain), Daerah Kawan (Kodomain), dan Daerah Hasil (Range)
3 Macam Himpunan
Pada bahasan himpunan dan diagram venn dikernal 3 macam himpunan yang meliputi himpunan semesta, himpunan bagian, dan himpunan kosong. Penjelasan ketiga macam himpunan tersebut diberikan seperti berikut.
Himpunan Semesta:
Himpunan semesta adalah himpunan yang memuat semua anggota himpunan. Notasi untuk himpunan semesta adalah S.
Himpunan Bagian:
A merupakan himpunan bagian B jika setiap anggota himpunan A merupakan anggota himpunan B. Notasi untuk menyatakan himpunan bagian adalah C. Simbol untuk menyatakan A himpunan bagian B adalah . Himpunan kosong merupakan himpunan bagian dari setiap himpunan. Setiap himpunan merupakan himpunan bagian dari himpunan itu sendiri.
Banyaknya anggota himpunan bagian dapat ditentukan dengan rumus 2n dengan n adalah banyak anggota himpunan.
Sebagai contoh terdapat sebuah himpunan A = {1, 2, 3}, di mana banyak anggota B meliputi 3 anggota sehingga n(A) = 3. Banyaknya himpunan bagian B adalah 23 = 8 yaitu { }; {1}; {2}; {3}; {1, 2}; {1, 3}; {2, 3}; {1, 2, 3}.
Himpunan Kosong:
Himpunan kosong adalah himpunan yang tidak mempunyai anggota. Himpunan kosong akan selalu menjadi himpunan bagian dari anggota himpunan bagian. Notasi himpunan kosong dapat dinyatakan dengan simbol { } atau ∅.
Baca Juga: Cara Menentukan Banyaknya Anggota Himpunan Bagian dengan n = 1, 2, 3, … Anggota
Hubungan Antar Himpunan
Pembahasan selanjutnya dalam materi himpunan dan diagram venn adalah hubungan antar himpunan. Hubungan antar himpunan meliputi irisan, gabungan, komplemen himpunan, dan selisih himpunan. Lebih lanjut mengenai keempatnya dapat dilihat seperti pembahasan di bawah.
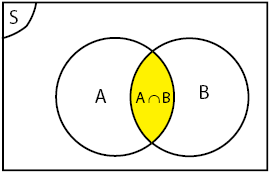
Irisan
Irisan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota A dan anggota B.
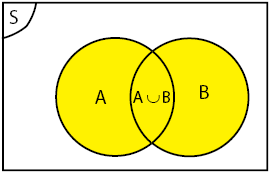
Gabungan
Gabungan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A atau anggota himpunan B.
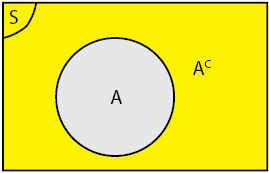
Komplemen
AC adalah himpunan yang anggota-anggotanya merupakan anggota himpunan semesta namun bukan anggota himpunan A.
Selisih
A − B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A namun bukan anggota himpunan B.

Baca Juga: Baris dan Deret Matematika
Sifat-Sifat Operasi Himpunan
Pembahasan dalam materi himpunan dan diagram venn meliputi juga sifa-sifat operasi pada himpunan. Sifat-sifat operasi himpunan meliputi komutatif, asosiatif, ditributif, dan dalil de Morgan. Penjelesan masing-masing sifat pada operasi himpunan diberikan seperti bahasan di bawah.
Komutatif:
A ∩ B = B ∩ A
A ∪ B = B ∪ A
Asosiatif:
(A ∩ B) ∩ C = A ∩ (B ∩ C)
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Distributif:
A ∩ ( B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = ( A ∪ B) ∩ (A ∪ C)
Dalil de Morgan:
(A ∩ B)C = AC ∪ BC
(A ∪ B)C = AC ∩ BC
Baca Juga: Kesebangunan pada Trapesium
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan himpunan dan diagram venn. Setiap contoh soal himpinan dan diagram venn yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Himpunan dan Diagram Venn
Diketahui:
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8}
Anggota himpunan A ∩ B adalah ….
A. {1, 2, 3, 4, 5, 6, 7, 8}
B. {1, 2, 3}
C. {4, 5}
D. {5}
Pembahasan:
Simbol irisan ∩ menandakan bahwa operasi untuk dua himpunan dengan anggota yang sama. Anggota himpunan A ={1, 2, 3, 4, 5} dan anggota himpunan B = {4, 5, 6, 7, 8}. Ada dua anggota himpunan A yang juga merupakan anggota himpunan B yaitu bilangan 4 dan 5. Sehingga, anggota himpunan A ∩ B adalah {4, 5}.
Jawaban: C
Contoh 2 – Soal Aplikasi Himpunan dan Diagram Venn
Kelas VII-A terdiri dari 31 siswa. Terdapat 15 siswa mengikuti kompetisi Matematika, 13 siswa mengikuti kedua kompetisi IPA, dan 7 siswa tidak mengikuti kompetisi tersebut. Banyak siswa yang mengikuti kedua kompetisi tersebut adalah ….
A. 28 siswa
B. 8 siswa
C. 5 siswa
D. 4 siswa
Pembahasan:
Misalkan:
x = banyak siswa yang mengikuti kedua kompetisi.
Himpunan tersebut dapat digambarkan dalam bentuk diagram venn seperti gambar di bawah.

Dari gambar diagram venn di atas dapat diperoleh persamaan untuk menghitung nilai x seperti yang ditunjukkan pada cara berikut.
Semua siswa = 31
x + 15 – x + 13 – x + 7 = 31
35 – x = 31
x = 4
Jadi, banyak siswa yang mengikuti kedua kompetisi tersebut adalah 4 siswa.
Jawaban: D
Demikianlah tadi ulasan materi tentang himpunan dan diagram venn yang meliputi sifat-sifat, macam-macam, serta contoh soal himpunan dan diagram venn dengan pembahasannya. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Terimakasih
Terima kasih jawabannya sangat lengkap
terima kasih
lengkap dan pembahasannya tuntas
jawaban lengkap.Mantap
jawabannya sangat lengkap