Jumlah Sudut – Sudut pada Segitiga

Segitiga adalah bangun ruang yang memiliki tiga titik sudut dan tiga sisi. Sisi pada segitiga merupakan ruas garis dari tiga ruas garis yang berbeda. Sedangkan sudut pada segitiga merupakan perpotongan antara dua ruas garis yang saling berpotongan pada satu titik. Antara panjang dan besar sudut pada segitiga memiliki hubungan sebanding, semakin besar sudut pada segitiga maka panjang sisi yang menghasap sudut tersebut akan semakin panjang.

Jenis segitiga meliputi banyak bentuk yang berbeda namun tetap dengan bagian yang terdiri atas tiga sisi dan tiga titik sudut. Jenis – jenis segitiga tersebut meliputi segitiga sama sisi, segitiga sama kaki, segitiga sembarang, segitiga siku – siku, segitiga tumpul, dan segitiga lancip. Perhatikan gambar dari berbagai jenis bentuk segitiga untuk lebih mengetahui bagaimana bentuk masing – masing jenis segitiga.

Meskipun jenis segitga yang beraneka ragam, terdapat kesamaan dari semua jenis-jenis segitiga yang telah disebutkan di atas. Apa kesamaan yang dimiliki jenis – jenis segitiga tersebut? Kesamaan tersebut berupa jumlah ketiga sudut pada segitiga yang selalu sama.

Berapa jumlah ketiga sudut segitiga? Sobat idschool dapat mencari tahu lebih banyak mengenai sudut-sudut pada segitiga melalui ulasan di bawah.

Table of Contents

• Berapa Jumlah Sudut – Sudut pada Segitiga?
• Contoh Soal Jumlah Sudut – Sudut pada Segitiga dan Pembahasan
  • Contoh 1 – Hubungan Besar Sudut dan Panjang Sisi pada Segitiga
  • Contoh 2 – Soal Jumlah Sudut – Sudut pada Segitiga

Baca juga: Teorema Pythagoras pada Segitiga Siku – Siku

Berapa Jumlah Sudut – Sudut pada Segitiga?

Jawaban atas pertanyaan di atas cukup singkat untuk dijawab. Jumlah sudut-sudut pada segitiga adalah 180^o. Namun dari mana angka tersebut diperoleh? Tentu saja angka tersebut diperoleh dari sebuah alasan.

Sebelum mengetahui bagaimana bisa jumlah sudut-sudut pada segitiga adalah 180^o, ingat kembali bahwa besar sudut pada garis lurus adalah 180^o. Sobat idschool dapat mengukur besar sudut pada garis lurus menggunakan busur derajat.

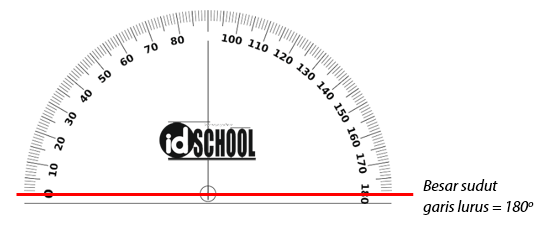
Apa hubungan antara jumlah sudut-sudut pada segitiga dengan besar sudut pada garis lurus? Simak lagi bahasan selanjutnya.

Akan dibuktikan bahwa jumlah sudut – sudut pada segitiga sama dengan 180^o. Pertama, buatlah sembarang segitiga ABC dengan ketiga sudut yang sobat idschool tidak perlu hitung terlebih dahulu. Nantinya, akan dibuktikan melalui percobaan sederhana bahwa jumlah kediga sudut segitiga tersebut adalah 180^o.

Potong masing – masing sudut sehingga didapat tiga buah potongan sudut segitiga tersebut. Potongan tiga sudut segitiga kemudian gabungkan menjadi satu. Gabungan ketiga sudut segitiga tersebut akan membentuk sebuah garis lurus. Sehingga, dapat diambil kesimpulan bahwa jumlah sudut – sudut pada segitiga sama adalah 180^o.

Sobat idschool bisa mencoba dengan bentuk segitiga yang sobat idschool buat sendiri. Dengan berbagai bentuk segitiga, nantinya gabungan ketiga sudut segitiga akan membentuk sebuah garis lurus.

Baca Juga: Apa Itu Gradien dan Bagaimana Cara Menentukan Nilainya?

Contoh Soal Jumlah Sudut – Sudut pada Segitiga dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Hubungan Besar Sudut dan Panjang Sisi pada Segitiga

Pada gambar berikut, segitiga PQR dan segitiga STU merupakan dua segitiga kongruen.

Besar ∠R = ∠U dan ∠Q = ∠S . Manakah pasangan sisi yang sama panjang?
A. PR = SU
B. QR = TU
C. PQ = SU
D. PQ = ST

Pembahasan:
Sisi yang sama panjang bersesuaian dengan besar sudut dalam segitiga. Artinya pada dua buah segitiga dengan sudut yang sama besar akan memiliki panjang sisi yang berhadapan dengan sudut tersebut sama panjang. Perhatikan kembali segitiga PQR dan STU berikut.

Pasangan sisi yang sama panjang adalah PQ = ST, QR = SU, dan PR = TU.

Jawaban: D

Baca Juga: Contoh Soal Segitiga dengan Teorema Pythagoras

Contoh 2 – Soal Jumlah Sudut – Sudut pada Segitiga

Perhatikan gambar!

Besar sudut BAC adalah …
A. 24^o
B. 28^o
C. 55^o
D. 65^o

Pembahasan:
Diketahui bahwa jumlah ketiga sudut segitiga sama dengan besar sudut garis lurus yaitu 180^o. Sehingga, dengan menjumlahkan ketiga sudut segitiga ABC dapat diperoleh nilai x seperti perhitungan berikut.

Menghitung nilai x:
∠A + ∠B + ∠C = 180^o
2x + 4^o + 4x + 7^o + 8x + 1^o = 180^o
2x + 4x + 8x + 4^o + 7^o + 1^o = 180^o
14x + 12^o = 180^o
14x = 180^o – 12^o
14x = 168^o
x = ¹⁶⁸/₁₄ = 12^o

Menghitung sudut BAC:
∠BAC = ∠A
∠BAC = 2x + 4^o
∠BAC = 2 × 12^o + 4^o = 24^o + 4^o = 28^o

Jadi, besar sudut BAC adalah 28^o.

Jawaban: B

Demikianlah tadi ulasan materi terkait jumlah sudut – sudut pada segitiga yang dilengkapi dengan contoh soal dan pembahasan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Kumpulan Soal UN SMP – Materi Segitiga dan Segi Empat