Ada dua jenis perbandingan yaitu perbandingan senilai dan berbalik nilai. Perbandingan senilai ditandai adanya kenaikan satu faktor yang diikuti kenaikan faktor lainnya. Sedangkan perbandingan berbalik nilai ditandai dengan kenaikan faktor yang membuat faktor lain turun.
Contoh perbandingan senilai adalah kebutuhan tepung untuk membuat kue, banyak pakan ternak, jumlah cat yang dibutuhkan. Contoh perbandingan berbalik nilai adalah banyak pekerja dengan waktu untuk menyelesaikannya, besar kecepatan dengan lama waktu tempuh, banyak ternak dengan waktu untuk menghabiskannya.
Pembahasan lebih banyak mengenai perbandingan senilai dan berbalik nilai ada di bawah.
Daftar isi:
- Perbandingan Senilai
- Perbandingan Berbalik Nilai
- Perbandingan Senilai dan Berbalik Nilai
- Soal Perbandingan Senilai dan Berbalik Nilai
Baca Juga: Jarak Pada Peta dan Jarak Sebenarnya
Perbandingan Senilai
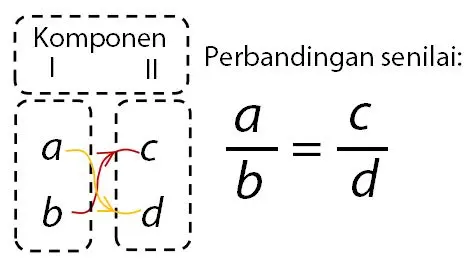
Rumus perbandingan senilai adalah perkalian silang antar dua faktor. Misalkan nilai untuk faktor pertama membutuhkan sejumlah a untuk membuat sejumlah b. Dan faktor kedua membutuhkan sejumlah c untuk membuat sejumlah d. Rumus perbandingan senilainya adalah ad = bc.
Atau, perbandingan senilai dapat dinyatakan dalam persamaan perbandingan a/b = c/d.
Contoh masalah perbandingan senilai adalah kebutuhan tepung untuk membuat kue. Semakin banyak kue yang akan dibuat, semakin banyak tepung terigu yang dibutuhkan. Kenaikan satu faktor membuat faktor lainnya naik.
Soal:
Untuk membuat 9 loyang kue diperlukan 6 kg tepung terigu. Tentukan banyak tepung terigu untuk membuat 12 loyang kue!
Jawab:
Data dari soal ada pada tabel berikut.
| Banyak kue (n) | Banyak tepung (w) | |
| I | 9 loyang | 6 kg |
| II | 12 loyang | x kg |
Keterangan: x = banyak tepung untuk membuat 12 loyang kue
Menentukan nilai x:
*lakukan kali silang
9x = 12 × 6
9x = 72
Jadi, banyak tepung terigu yang diperlukan adala x = 8 kg.
Baca Juga: Perbandingan Tiga Bilangan
Perbandingan Berbalik Nilai
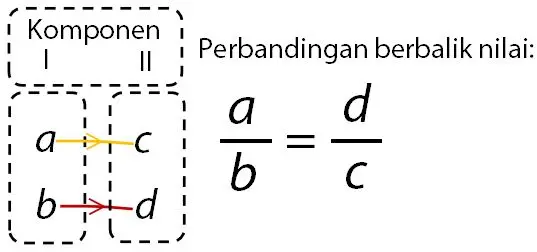
Rumus perbandingan berbalik nilai adalah perkalian sejajar antara dua faktor. Misalkan faktor pertama membutuhkan sejumlah a untuk memenuhi kebutuhan sejumlah b. Dan faktor kedua membutuhkan sejumlah c untuk memenuhi kebutuhan sejumlah d.
Rumus perbandingan berbalik nilai yang digunakan adalah ac = bd. Atau persamaan perbandingan berbalik nilai dapat juga menggunakan a/b = d/c.
Contoh masalah perbandingan berbalik nilai adalah kebutuhan banyak pekerja dengan jumlah hari. Seperti contoh soal di bawah.
Soal:
Seorang pemborong mampu menyelesaikan pekerjaannya selama 49 hari dengan 64 pekerja. Karena sesuatu hal, pekerjaan itu harus selesai dalam waktu 28 hari. Tentukan banyak pekerja yang harus ditambah!
Jawab:
Dari soal diketahui beberapa informasi berikut.
| Waktu (W) | Banyak pekerja (n) | |
| I | 49 | 64 |
| II | 28 | 64 + x |
Keterangan:
x = banyak pekerja tambahan yang dibutuhkan
Sehingga,
*lakukan kali silang
28(64 + x) = 49×64
28 × 64 + 28x = 49×64
1.792 + 28x = 3.136
28x = 3.136 − 1.792 = 1.344
x = 48
Jadi, banyak pekerja yang harus ditambah adalah x = 48 pekerja.
Baca Juga: Rumus Luas Sebenarnya
Perbandingan Senilai dan Berbalik Nilai
Perlu diingat bahwa rumus perbandingan senilai adalah perkalian silang. Sedangkan rumus perbandingan berbalik nilai adalah perkalian sejajar.
Rumus perbandingan senilai dan berbalik nilai di atas berguna untuk menyelesaikan contoh soal di bawah.
Soal:
Sebanyak 24 kg beras cukup untuk makan 6 orang selama 4 hari. Berapa kg beras yang dibutuhkan untuk mencukupi makanan 8 orang selama 6 hari?
Jawab:
Kebutuhan beras dengan banyak orang makan merupakan perbandingan senilai. Sementara kebutuhan beras dengan lama hari adalah perbandingan berbalik nilai.
Misalkan banyak beras yang akan dicari = x maka dapat disusun bentuk perbandingan seperti berikut.
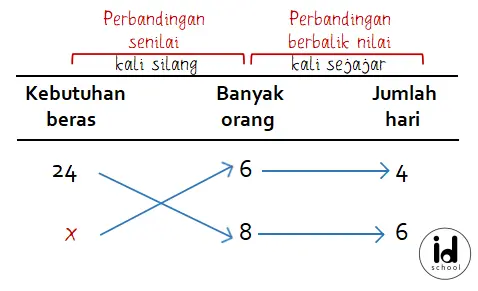
Kalikan sesuai anak panahnya.
Sehingga, 24 × 8 × 6 = x × 6 × 4
x = 8 × 6 = 48 kg
Jadi, banyak beras yang dibutuhkan untuk mencukupi makanan 8 orang selama 6 hari adalah 9 kg.
Baca Juga: Kesebangunan dan Kekongruenan
Soal Perbandingan Senilai dan Berbalik Nilai
Beberapa contoh soal perbandingan senilai dan berbalik nilai ada di bawah.
Contoh 1 – Lama waktu melakukan suatu pekerjaan
Suatu pekerjaan dapat diselesaikan oleh 40 orang dalam Waktu 44 hari. Setelah dikerjakan selama 20 hari, pekerjaan dihentikan selama 12 hari. Jika pekerjaan itu ingin diselesaikan tepat pada waktunya, maka banyaknya pekerja tambahan yang dibutuhkan adalah ….
A. 88 orang
B. 60 orang
C. 48 orang
D. 40 orang
Pembahasan:
Pekerjaan telah dikerjakan selama 20 hari dan berhenti selama 12 hari. Banyak hari yang tersisa untuk mengerjakan pekerjaan agar sesuai target awal = 44 hari – 20 hari – 12 hari = 12 hari.
Pada kondisi normal, pekerjaan dalam 24 hari dikerjakan oleh 40 orang. Saat waktu yang diberikan hanya 12 hari, banyaknya pekerja yang mengerjakan = x orang.
| Kondisi | Banyak Pekerja | Waktu |
| A | 40 orang | 24 hari |
| B | x | 12 hari |
Sehingga,
Pekerja A × waktu A = Pekerja B × waktu B
40 × 242 = x × 121
x = 2 × 40 = 80 orang
Diketahui sudah ada 40 orang yang sudah bekerja sebelumnya. Jadi, banyaknya pekerja yang dibutuhkan = 80 orang – 40 orang = 40 orang.
Jawab: D
Contoh 2 – Banyak waktu yang dibutuhkan pekerja
Pekerjaan membangun sebuah warung dapat diselesaikan oleh Pak Zulkifli dalam 30 hari. Sementara Pak Sahlan dapat menyelesaikannya dalam 20 hari.
Waktu yang diperlukan untuk membangun warung tersebut jika mereka bekerja bersama adalah ….
A. 50 hari
B. 25 hari
C. 12 hari
D. 10 hari
Pembahasan:
Dari soal diketahui beberapa informasi berikut.
- Waktu Pak Zulkifli: t1 = 30 hari
- Waktu Pak Sahlan: t2 = 20 hari
Misal:
t = waktu yang diperlukan Pak Zulkifli dan Pak Sahlan
Menghitung nilai t: