Persamaan Garis Lurus yang Saling Tegak Lurus

Persamaan garis lurus yang saling tegak lurus dapat diketahui dari hasil perkalian gradien dari kedua garis sama dengan –1. Atau, jika garis pertama memiliki gradien m₁ dan garis kedua memiliki gradien m₂ maka perkalian gradien kedua garis tersebut memenuhi persamaan m₁ × m₂ = ‒1. Dapat juga dikatakan bahwa persamaan garis lurus yang saling tegak lurus memiliki nilai gradien dengan sifat berlawanan dan berkebalikan,

Sebuah garis lurus yang berpotongan dengan sebuah garis lurus lainnya akan memiliki sebuah titik potong dengan besar sudut yang dibentuk tidak selalu tegak lurus. Dua buah garis dikatakan tegak lurus jika sudut yang dibentuk oleh perpotongan kedua garis sama dengan 90^o (siku-siku).

Baca Juga: Cara Menentukan Persamaan Garis Jika Diketahui Melalui Dua Titik

Bagaimana cara mengetahui dua buah garis lurus yang saling tegak lurus? Bagaimana persamaan garis lurus yang saling tegak lurus? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.

Table of Contents

• Hubungan Gradien dari Dua Garis Saling Tegak Lurus
• Cara Cepat Menemukan Persamaan Garis Lurus yang Saling Tegak Lurus
• Contoh Soal dan Pembahasan
  • Contoh 1 – Persamaan Garis Lurus yang Saling Tegak Lurus
  • Contoh 2 – Persamaan Garis Saling Tegak Lurus

Hubungan Gradien dari Dua Garis Saling Tegak Lurus

Hal perlu diingat untuk menyatakan dua garis lurus yang saling tegak lurus adalah hasil kali gradien dari kedua garis sama dengan sama dengan –1. Dari karakteristik nilai gradien inilah, nantinya sobat idschool dapat menentukan persamaan garis yang tegak lurus dengan suatu garis lainnya.

Misalkan terdapat dua buah garis dengan nilai gradien garis pertama adalah m_g1 dan nilai gradien garis kedua sama dengan m_g2. Hasil kali kedua gradien tersebut akan sama dengan – 1.

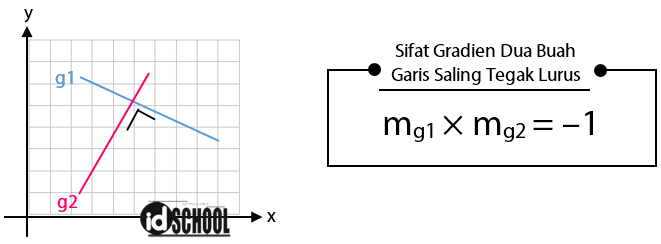
Jika diketahui garis g₂ melalui titik (x₁, y₁) dan tegak lurus dengan garis g₁ maka untuk mencari persamaan garis lurus yang saling tegak lurus dapat menggunakan persamaan berikut.

Di mana nilai m_g2 adalah nilai gradien dari gradies ke dua atau gradien garis yang akan dicari persamaan garisnya. Secara singkat, cara menemukan persamaan garis lurus yang saling tegak lurus sesuai dengan langkah-langkah berikut.

1. Menentukan gradien garis pertama (m_g1) yaitu garis yang akan tegak lurus dengan garis yang akan dicari persamaannnya
2. Menentukan gradien garis kedua (m_g1) yairu garis yang akan dicari persamaannya
   Gradien garis pertama adalah lawan kebalikan dari gradien garis kedua atau memenuhi persamaan m_g1 × m_g2 = –1. Misalkan m_g1 = 3 maka gradien garis kedua sama dengan m_g2 = ‒¹/₃
3. Perhatikan sebuah titik yang dilalui garis ke dua yaitu titik (x₁, y₁)
4. Substitusi nilai gradien m_g2 dan titik (x₁, y₁) yang dilalui gari pada persamaan y – y₁ = m(x – x₁)
5. Lakukan operasi aljabar biasa sehingga diperoleh persamaan garis lurus yang saling tegak lurus dengan suatu garis

Bagian contoh soal dan pembahasan di akhir bagian akan menunjukkan bagaimana proses mendapatkan persamaan garis lurus yang saling tegak lurus seperti langkah-langkah di atas.

Baca Juga: Garis Istimewa pada Segitiga

Cara Cepat Menemukan Persamaan Garis Lurus yang Saling Tegak Lurus

Selain cara seperti langkah-langkah yang telah diberikan di atas, ada juga sebuah cara cepat yang dapat digunakan untuk menentukan persamaan garis lurus yang saling tegak lurus. Cara cepat ini sebaiknya sobat idschool sudah menguasai bagaimana cara menentukan persamaan garis yang saling tegak lurus dengan cara langkah per langkah. Karena bagaimanapun juga, pemahaman konsep materi secara menyeluruh akan selalu lebih baik dari pada hanya paham cara yang instan.

Lalu bagaimana cara cepat menentukan persamaan garis lurus yang saling tegak lurus dengan garis lain? Perhatikan caranya melalui penjelasan berikut.

Kesimpulannya:
(i) Persamaan garis ax + by + c = 0 akan tegak lurus dengan garis bx – ay = b × x₁– a × y₁
(ii) Persamaan garis ax – by + c = 0 akan tegak lurus dengan garis bx + ay = b × x₁+ a × y₁
Di mana, x₁ dan y₁ berturut-turut adalah titik absis dan ordinat yang diketahui dilalui oleh garis tersebut.

Baca Juga: Cara Menentukan Persamaan Garis Lurus yang Saling Sejajar

Contoh Soal dan Pembahasan

Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!

Contoh 1 – Persamaan Garis Lurus yang Saling Tegak Lurus

Persamaan garis yang melalui titik (4, 2) dan tegak lurus dengan garis 2x – y + 5 = 0 adalah ….
A. x + 2y + 6 = 0
B. x – 2y – 8 = 0
C. 2x – y – 6 = 0
D. x + 2y – 8 = 0

Pembahasan:
Pertama, akan dikerjakan dengan cara step by step, kemudian akan dibandingkan hasilnya dengan cara cepat.

Cara Step by Step:
1) Menentukan gradien dari garis 2x – y + 5 = 0

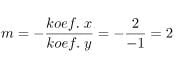
Karena yang akan dicari adalah garis yang tegak lurus dengan garis 2x – y + 5 = 0 maka nilai gradien garis yang akan dicari adalah lawan kebalikan dari gradien garis tersebut, yaitu m = ‒¹/₂

2) Menentukan gradien garis kedua
Perhatikan cara mendapatkan nilai gradien garis kedua yang saling tegak lurus dengan garis 2x – y + 5 seperti berikut.
m₁ × m₂ = ‒1
2 × m₂ = ‒1
m₂ = ‒¹/₂

Selanjutnya, gunakan nilai gradien dari hasil perhitungan di atas untuk mendapatkan persamana garis yang tegak lurus dengan gari 2x – y + 5 = 0. Diketahui persamaan garis yang akan dicari melalui titik (4, 2) maka persamaan garis yang akan dicari dapat diperoleh seperti cara di bawah.

3) Menentukan persamaan garis lurus yang saling tegak lurus dengan garis 2x – y + 5 = 0:
y – y₁ = m₂ ( x – x₁ )
y – 2 = –¹/₂ ( x – 4 )
2 ( y – 2 ) = –( x – 4 )
2y – 4 = –x + 4
x + 2y – 4 – 4 = 0
x + 2y – 8 = 0

Jadi, persamaan garis yang melalui titik (4, 2) dan tegak lurus dengan garis 2x – y + 5 = 0 adalah x + 2y – 8 = 0.

Bandingkan hasilnya dengan cara cepat berikut.

Cara cepat:
Diketahui bahwa persamaan garis yang akan dicari melalui titik (4, 2) maka x₁ = 4 dan y₁ = 2.

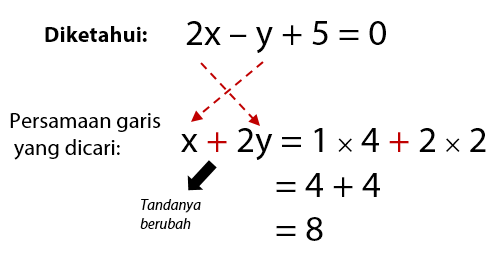
Diperoleh persamaan garis x + 2y = 8 → x + 2y – 8 = 0 (hasil yang sama dengan cara step by step)

Jadi, persamaan garis yang melalui titik (4, 2) dan tegak lurus dengan garis 2x – y + 5 = 0  adalah x + 2y – 8 = 0.

Jawaban: D

Baca Juga: 4 Cara Menentukan Gradien Garis Lurus

Contoh 2 – Persamaan Garis Saling Tegak Lurus

Perhatikan gambar di bawah!

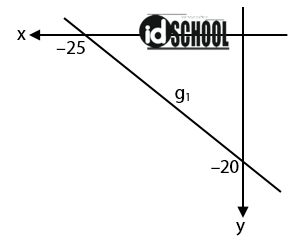
Persamaan garis yang tegak lurus dengan garis g₁ dan melalui titik (0, – 20) adalah ….
A.   5x – 4y = 80
B. 4x – 5y = 80
C. 5x + 4y = 80
D. 4x + 5y = 80

Pembahasan:
Langkah pertama adalah mencari nilai gradien garis g₁: Garis yang diberikan pada gambar condong ke kiri, sehingga gradiennya bernilai negatif.

m₁ = ‒^Δy/_Δx
m₁ = ‒²⁰/₂₅ = ‒⁴/₅

Mencari gradien garis kedua, karena tegak lurus maka berlaku hasil kali perkalian gradiennya sama dengan – 1.
m₁ × m₂ = –1
–⁴/₅ × m₂ = –1
m₂ = –1 × –⁵/₄
m₂ = ⁵/₄

Mencari persamaan garis lurus yang saling tegak lurus dengan garis g₁ dan melalui titik (0, – 20):
y – y₁ = m₂( x – x₁ )
y – (-20) = ⁵/₄( x – 0 )
y + 20 = ⁵/₄ x
4( y + 20 ) = 5x
4y + 80 = 5x
5x – 4y = 80

Jadi persamaan garis lurus yang saling tegak lurus dengan garis g₁ dan melalui titik (0, – 20) adalah 5x – 4y = 80.

Jawaban: A

Demikianlah tadi ulasan materi cara menentukan persamaan garis lurus yang saling tegak lurus. Meliputi juga cara cepat menemukan persamaan garis saling tegak lurus dan contoh soal beserta dengan pembahasannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.

Baca Juga: Rumus pada Persamaan Garis Lurus