Rumus mencari bunga dalam Matematika digunakan untuk menyelesaikan berbagai tipe soal yang berkaitan dengan tabungan atau pinjaman. Jenis bunga dalam masalah tabungan/pinjaman terdiri dari 2 macam yaitu bunga tunggal dan bunga majemuk.
Bunga tunggal adalah bunga yang timbul pada setiap akhir jangka waktu tertentu yang tidak mempengaruhi besarnya modal yang dapat berupa pinjaman/tabungan (besarnya modal tetap). Sedangkan bunga majemuk adalah adalah bunga yang dihitung berdasarkan pokok awal, yang juga mencakup semua bunga akumulasi dari deposito atau pinjaman periode sebelumnya
Pada bahasan tingkat dasar dan menengah, perhitungan bunga menggunakan jenis bunga tunggal, Sehingga, bahasan di bawah akan lebih banyak mengulas mengenasi bunga tunggal. Secara sederhana, besar bunga tunggal sama dengan besar persentase bunga dikali tabungan/pinjaman awal.
Dalam prakteknya ada beberapa variasi soal yang sobat idschool akan jumpai. Dan aneka tipe soal yang diberikan pada dasarnya hanya memerlukan rumus dasar tersebut. Namun, sobat idschool juga dapat menggunakan rumus-rumus yang telah diturunkan seperti tabel di bawah.

Baca Juga: Cara Menghitung Harga Sebelum Diskon
Dari mana rumus mencari bunga tersebut diperoleh? Bagaiman penggunaan rumus-rumus tersebut untuk menentukan besar bunga tabungan atau pinjaman? Sobat idschool dapat mencari tahu jawabannya melalui ulasan di bawah.
Table of Contents
Rumus Mencari Bunga
Dalam bahasan rumus mencari bunga dalam matematika, ada beberapa tipe soal yang biasa diberikan. Pada dasarnya, bahasan yang diulas berupa menentukan besar bunga yang harus dibayar. Besar bunga yang harus dibayar tergantung persentase yang diberikan. Rumus mencari bunga ini kemudian dapat dimodifikasi untuk berbagai jenis tipe soal.
Ada dua jenis type soal menentukan bunga.
Pertama
adalah rumus mencari bunga untuk persoalan yang diketahui tabungan awal, persentase bunga per tahun, dan lama meminjam selama satu tahun.
Kedua:
merupakan pengembangan dari jenis pertama. Persoalan yang diketahui meliputi tabungan awal, persentase bunga per tahun, dan lama meminjam selama n bulan. Besar bunga diperoleh dari persentase bunga dikali tabungan awal yang dimiliki.
Berikut ini adalah rumus bunga jika diketahui tabungan awal (Tab. Awal), besar persentase bunga per tahun (p), dan lama menabung adalah satu tahun.
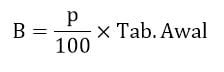
Untuk lama menabung diketahui selama n bulan, berikut ini adalah rumus mencari bunga dalam matematika yang dapat digunakan.
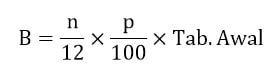
Baca Juga: Rumus dan Cara Menentukan Besar Bruto, Netto, dan Tara
Menghitung Tabungan Akhir
Rumus yang dapat digunakan untuk menghitung tabungan akhir dapat diperoleh dengan menambahkan tabungan awal dengan besar bunga. Namun di sini akan diberikan rumus instan mencari tabungan untuk menentukan besar tabungan akhir.
Diketahui tabungan awal (Tab. Awal) dan persentase bunga per tahun (p). Berikut ini adalah langkah – langkah penurunan rumusnya.

Sehingga diperoleh rumus instant untuk menghitung besar tabungan akhir seperti persamaan berikut.

Dengan mengikuti cara yang sama dapat diperoleh rumus besar tabungan akhir untuk lama menabung selama n bulan.

Baca Juga: Aritmetika Sosial
Menghitung Tabungan Awal
Rumus yang dapat digunakan untuk menghitung tabungan awal adalah besar tabungan akhir dikurangi besar bunga. Seperti dengan rumus mencari tabungan akhir di atas, untuk mencari besar tabungan awal juga ada rumus instannya.
Diketahui tabungan akhir (Tab. Akhir) dan persentase bunga per tahun (p). Berikut ini adalah langkah – langkah penurunan rumus tabungan awal.
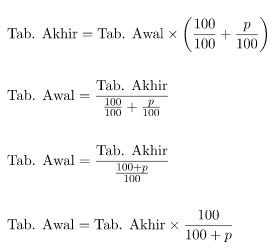
Sehingga diperoleh rumus instant untuk menghitung besar tabungan awal sesuai persamaan di bawah.
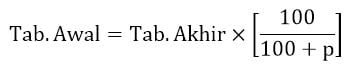
Dengan mengikuti cara yang sama dapat diperoleh rumus besar tabungan awal untuk lama menabung selama n bulan.

Baca Juga: Macam-Macam Konversi Satuan
Menentukan Lama Menabung
Penurunan rumus mencari bunga dalam Matematika untuk menentukan lama menabung juga diperoleh dari turunan rumus sebelumnya. Langkah – langkan penurunan rumus mencari bunga dalam matematika adalah sebagai berikut.

Diperoleh rumus menentukan lama menabung seperti persaman berikut ini.

Keterangan:
n = lama menabung (bulan)
p = persentase bunga per tahun (persen)
Baca Juga: Rumus Keliling dan Luas Belah Ketupat
Menentukan Persentase Bunga
Rumus mencari bunga dalam Matematika bagian mencari nilai persentase juga dapat diturunkan dari rumus sebelumnya. Rumus besar persentase bunga dapat dihitung melalui persamaan di bawah.
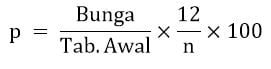
Keterangan:
n = lama menabung (bulan)
p = persentase bunga per tahun (persen)
Baca Juga: Persentase Untung – Rugi
Contoh Soal dan Pembahasan
Beberapa tipe soal terkait rumus mencari bunga dalam matematika yang akan diberikan di sini meliputi 5 jenis soal yang berbeda. Yaitu menghitung besar bunga bank, menghitung tabungan akhir, menghitung besar tabungan awal, menentukan lama menabung, dan menentukan besar persentase bunga yang diberikan.
Contoh 1 – Menghitung Besar Bunga Bank
Satria meminjam uang di Bank sebesar Rp750.000,00. Diketahui besar bunga yang harus dibayarkan adalah 12% per tahun. Bunga yang harus dibayar Satria dalam satu tahun adalah ….
A. Rp60.000,00
B. Rp75.000,00
C. Rp90.000,00
D. Rp105.000,00
Pembahasan:
Besar bunga yang harus dibayar Satria dalam satu tahun dapat dihitung seperti langkah pada penyelesaian berikut.
Bunga = 12/100 × 750.000
= Rp90.000,00
Jadi, Bunga yang harus dibayar Satria dalam satu tahun adalah Rp90.000,00.
Jawaban: C
Contoh 2 – Menghitung Besar Tabungan Akhir
Ibu menabung di bank sebesar Rp2.500.000,00 dengan bunga 10% pertahun.
Jika lama ibu menabung di bank tersebut adalah 8 bulan maka besar tabungan ibu sekarang adalah ….
A. Rp2.750.000,00
B. Rp2.800.000,00
C. Rp2.850.000,00
D. Rp2.900.000,00
Pembahasan:
Tabungan akhir ibu setelah 8 bulan dapat dihitung seperti pada penyelesaian cara berikut.

Jadi, jika lama ibu menabung di bank tersebut adalah 8 bulan maka besar tabungan ibu sekarang adalah Rp2.750.000,00.
Jawaban: A
Baca Juga: Perbandingan Senilai dan Berbalik Nilai
Contoh 3 – Menghitung Besar Tabungan Awal
Shania menabung di bank selama 5 bulan dengan bunga 10%. Shania mengetahui besar tabungan menjadi Rp3.200.000,00. Besar tabungan awal Shania adalah ….
A. Rp3.720.000,00
B. Rp3.702.000,00
C. Rp3.270.000,00
D. Rp3.072.000,00
Pembahasan:
Tabungan awal Shania dapat dihitung seperti pada cara penyelesaian berikut.

Jadi, besar tabungan awal Shania adalah Rp3.072.000,00.
Jawaban: D
Contoh 4 – Menentukan Lama Menabung
Ani menabung di Bank sebesar Rp500.000,00 dengan bunga per tahun 9%. Saat Ani mengambil uangnya, besar tabungan Ani adalah Rp537.500,00. Lama Ani menabung di bank adalah ….
A. 8 bulan
B. 9 bulan
C. 10 bulan
D. 11 bulan
Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.
Tabungan awal: Taw = Rp500.000,00
Tabungan akhir: Tak = Rp537.500,00
Besar bunga yang diterima Ani dapat dihitung melalui cara tabungan akhir dikurang tabungan awal:
Bunga = 537.500 – 500.000
Bunga = 37.500
Menghitung berapa lama Ani menabung (n) di bank:

Jadi, lama Ani menabung (n) di bank adalah 10 bulan.
Jawaban: C
Contoh 5 – Menentukan Besar Persentase Bunga yang diberikan
Susanti menabung di bank selama 3 bulan dengan besar tabungan awal senilai Rp1.200.000,00. Saat Susanti mengambil uangnya, besar tabungan Susanti adalah Rp1.237.500,00. Persentase bunga yang didapat Susanti adalah ….
A. 10%
B. 12,5%
C. 15%
D. 17,5%
Pembahasan:
Cara menghitung besar persentase bunga yang didapat Susanti dapat dilakukan seperti cara berikut.

Jadi, persentase bunga yang didapat Susanti adalah 12,5%.
Jawaban: B
Demikianlah ulasan rumus mencari bunga dalam matematika dan contoh soalnya. Meliputi contoh soal dengan berbagai tipe seperti menghitung besar bunga bank, menentukan lama menabung, dan menentukan besar angsuran yang harus dibayarkan. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Ada yang bisa jawab contohnya andi menabung di bank 5 juta dengan bunga 6% pertahun berapa jumlah uangnya( uang pokok+ bunga) selama 7 tahun andi menabung di bank
A.bila bunga yang di bayarkan sekali setahun
B.bila bunga di bayarkan pertriwulan
C.bila bunga di bayarkan secara kontinyu pertahun
Tolong donk jawab kalo ada yang bisa