Cara Menghitung Mean Data Kelompok +Contoh Soalnya

Mean merupakan salah satu nilai ukuran pemusatan data. Nilai mean (x̅) adalah nilai rata-rata dari beberapa kumpulan datum (data). Cara menghitung mean data kelompok menggunakan rumus x̅ = Ʃx_i · f_i/Ʃf_i atau x̅ = x̅_s + Ʃf_i·d_i/Ʃf_i.

Rumus Mean Data Kelompok

Rumus mean data kelompok yang pertama secara umum sama dengan mean data tunggal. Yaitu jumlah semua nilai dibagi banyak frekuensi. Ada dua rumus yang dapat digunakan untuk menghitung mean data kelompok.

Bagaimana cara menghitung mean data kelompok ada pada penyelesaian soal-soal di bawah.

Daftar isi:

• Soal 1: Menghitung Mean Data Kelompok dari Tabel
• Soal 2: Mean Data Kelompok dengan Rataan Sementara
• Soal 3: Mean Data Kelompok dari Histogram
• Soal 4: Nilai p = ….
• Soal 5 – Jika berat Andi 62 kg maka berat siswa …
• Soal 6 – Perbandingan Banyak Siswa
• Soal 7 – Nilai rata-rata dari 9 nilai pengamatan tersebut adalah …

Baca Juga: Kumpulan Rumus Mean Median Modus Data Kelompok + Contoh Soalnya

Soal 1: Menghitung Mean Data Kelompok dari Tabel

Data berat badan dari 50 siswa disajikan pada tabel berikut.

Rata-rata berat siswa adalah ….
A. 61,8 kg
B. 62,0 kg
C. 62,5 kg
D. 63,2 kg
E. 64,2 kg

Pembahasan:
Rata-rata berat siswa sama dengan nilai mean data kelompok dari penyajian data kelompok dalam tabel.

• Langkah-langkah:
  • Menentukan nilai titik tengah (x_i)
  • Menghitung dan hasil kali x_i dengan f_i di setiap kelas
  • Dapat diperoleh banyak data (Ʃf_i) dan jumlah perkalian x_i dan f_i (Ʃx_i·f_i)
  • Mencari nilai mean (rata-rata)

Cara menghitung nilai mean data kelompok pada tabel:

Jadi, rata-rata berat siswa adalah 63,2 kg.

Jawaban: D

Baca Juga: Rumus Permutasi dan Contoh Soalnya

Soal 2: Mean Data Kelompok dengan Rataan Sementara

Perhatikan tabel berikut!

Jika rata-rata sementara adalah 27 maka nilai rata-rata data tersebut adalah ….

Pembahasan:
Cara menghitung nilai mean data kelompok dengan nilai rata-rata sementara meliputi langkah-langkah berikut.

1. Mencari titik tengah pada setiap interval kelas (x_i)
2. Menentukan nilai rata-rata sementara (x_s). Jika diketahui bisa menggunakan nilai yang dinfokan.
3. Menghitung nilai di melalui persamaan d_i = x_i – x_s
4. Menghitung perkalian nilai d_i dan f_i
5. Menjumlah perkalian antara d_i dan f_i (Σ d_i × f_i)
6. Menjumlah frekuensi pada setiap kelas (Σ f_i)
7. Substitusi x_s, Σ d_i × f_i, dan Σ f_i pada rumus mean data kelompok
8. Diperoleh nilai mean data kelompok

Pada soal diketahui nilai rata-rata sementara adalah x_s = 27. Data untuk nilai tengah (x_i) dan selisih nilai tengah dengan nilai rataan sementara (d_i) terdapat pada tabel berikut.

Nilai mean data koelompok di atas adalah

Jadi, nilai rata-rata data tersebut adalah 27 + (^–165/₅₀)

Jawaban: B

Baca Juga: Peluang Kejadian Majemuk dan Bersyarat

Soal 3: Mean Data Kelompok dari Histogram

Berat badan siswa pada suatu kelas disajikan dengan histogram seperti gambar di bawah ini.

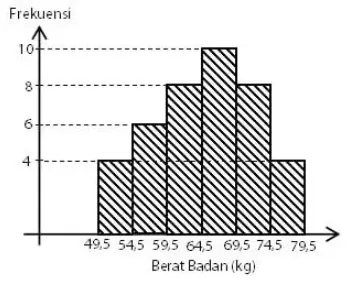
Rataan berat badan pada data tersebut adalah ….
A. 64,5 kg
B. 65,0 kg
C. 65,5 kg
D. 66 kg
E. 66,5 kg

Pembahasan:
Menentukan nilai titik tengah (x_i) dan frekuensi (f_i) untuk setiap kelas dari penyajian histogram data kelompok.

Tabel hasil kali titik tengah (x_i) dengan frekuensi (f_i) setiap kelas:

Menghitung jumlah x_i · f_i:

Σx_i · f_i = x₁ · f₂ + x₂ · f₂ + x₃ · f₃ + x₄ · f₄ + x₅ · f₅ + x₆ · f₆

Σx_i · f_i = 208 + 342 + 496 + 670 + 576 + 308 = 2.600

Menghitung nilai rata-rata berat bada siswa:

Jadi, rataan berat badan pada data tersebut adalah 65,0 kg.

Jawaban: B

Soal 4: Nilai p = ….

Diketahui nilai rata-rata dari data yang disajikan dalam bentuk histogram di bawah adalah 55,8.

Nilai p = ….
A. 8
B. 9
C. 10
D. 12
E. 13

Pembahasan:
Dari histogram dapat diketahui nilai tengah dan frekuensi setiap kelas seperti pada tabel berikut.

Berdasarkan keterangan nilai titik tengan (x_i) dan frekuensinya (f_i) yang diberikan pada soal dapat dibentuk persamaan berikut (diketahui nilai mean x = 55,8).

55,8(30 + 2p) = 1.550 + 124p

124p − 111,6p = 1.674 − 1.550

12,4p = 124

Jadi, nilai frekuensi untuk kelas ke-6 jika diketahui rata-rata 55,8 adalah p = 10.

Jawaban: C

Baca Juga: Cara Menghitung Kuartil Atas, Tengah, dan Bawah dari Data Kelompok

Soal 5 – Jika berat Andi 62 kg maka berat siswa …

Berat rata-rata 10 siswa adalah 60 kg. Salah seorang diantaranya diganti oleh Andi sehingga berat rata-ratanya menjadi 60,5 kg. Jika berat Andi 62 kg maka berat siswa yang diganti adalah ….
A. 57
B. 56
C. 55
D. 54
E. 53

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Rata-rata berat dari 10 siswa = 60 kg
• Rata-rata berat 9 siswa dan Andi = 60,5 kg
• Berat Andi: 62 kg

Misalkan, berat badan dari 10 orang siswa = x₁, x₂, …, dan x₁₀ 

Maka dapat dibentuk persamaan,

x₁ + x₂ + … + x₁₀ = 60 × 10

x₁ + x₂ + … + x₁₀ = 600

Misalkan berat badan siswa yang diganti oleh Andi adalah x₁₀ maka,

x₁ + x₂ + …+ x₉ + Andi = 60,5 × 10

x₁ + x₂ + …+ x₉ + 62 = 605

Segingga,

x₁ + x₂ + … + x₉ = 605 – 62

x₁ + x₂ + … + x₉ = 543

Degan demikian dapat diperoleh berat badan siswa yaitu,

x₁ + x₂ + … + x₉ + x₁₀ = 600

543 + x₁₀ = 600

x₁₀ = 600 – 543 = 57 kg

Jadi, berat siswa yang diganti adalah x₁₀ = 57 kg.

Jawaban: A

Baca Juga: Baca Juga: Rumus Kombinasi dan Contoh Cara Menggunakannya

Soal 6 – Perbandingan Banyak Siswa

Nilai rata-rata ulangan kelas A adalah x_A dan kelas B adalah x_B. Setelah kedua kelas digabung, nilai rata-ratanya adalah x. Jika x_A : x_B = 10 : 9 dan x : x_B = 85 : 81 maka perbandingan banyak siswa A dan B adalah ….
A. 8 : 9
B. 4 : 5
C. 3 : 4
D. 3 : 5
E. 9 : 10

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Nilai rata-rata ulangan kelas A = x_A
• Nilai rata-rata ulangan kelas B = x_B 
• Gabungan rata-rata nilai kelas A dan B = x
• x_A : x_B = 10 : 9
• x : x_B = 85 : 81

Menentukan perbandingan x_A, x_B, dan x:

x_A : x_B = 10 : 9 = 90 : 81

x : x_B = 85 : 81

Sehingga,

x_A : x_B : x = 90 : 81 : 85

Misalkan banyak siswa kelas A adalah n_A dan banyak siswa kelas B adalah n_B maka n = n_A + n_B.

Sehingga,

n_A • x_A + n_B • x_B = n • x

n_A • 90 + n_B • 81 = (n_A + n_B) • 85

90n_A + 81n_B = 85n_A + 85n_B

90n_A – 85n_A = 85n_B – 81n_B

5n_A = 4n_B → n_A : n_B = 4 : 5

Jadi, perbandingan banyak siswa A dan B adalah 4 : 5

Jawaban: B

Soal 7 – Nilai rata-rata dari 9 nilai pengamatan tersebut adalah …

Diketahui rata-rata dari 9 nilai pengamatan sama dengan dua kali median. Jika jumlah nilai pengamatan yang lebih kecil daripada median adalah 106 dan jumlah nilai pengamatan yang lebih besar dari median adalah 200, maka nilai rata-rata dari 9 nilai pengamatan tersebut adalah ….
A. 17
B. 18
C. 34
D. 36
E. 38

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Rata-rata dari 9 nilai pengamatan = 2 × Median
• Jumlah nilai pengamatan yang lebih kecil daripada median = 106
• Jumlah nilai pengamatan yang lebih besar dari median = 200

Misalkan 9 nilai pengamatan yang sudah diurutkan dari yang terkecil adalah x₁, x₂, …, dan x₉. Sehingga:

• Nilai median = x₅
• x₁ + x₂ + x₃ + x₄ = 106
• x₆ + x₇ + x₈ + x₉ = 200

Dapat diperoleh nilai x₅ (median) melalui persamaan berikut:

306 + x₅ + = 18x₅

18x₅ − x₅ = 306

Jadi, nilai rata-rata dari 9 nilai pengamatan tersebut adalah 2 × x₅ = 2 × 18 = 36.

Jawaban: D

Demikianlah ulasan cara menghitung mean data kelompok. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!