Menghitung Median Data Kelompok +7 Contoh Soal

Cara menghitung median data kelompok diawali dengan menentukan di mana letak kelas nilai median. Di mana letak kelas nilai median berada pada data ke–(ⁿ/₂ + 1) untuk jumlah data ganjil dan antara ke–(ⁿ/₂) dengan ke–(ⁿ/₂ + 1) untuk data genap. Selanjutnya cara menghitung nilai median data kelompok menggunakan rumus median untuk data kelompok.

Rumus median data kelompok adalah Md = Tb + {(ⁿ/₂ − fkk)/fi} × ℓ. Di mana Tb = batas bawah kelas nilai median, n = banyak data, fkk = frekuensi komulatif kurang dari kelas median, dan fi = frekuensi kelas median.

Untuk menggunakan rumus median data kelompok perlu untuk mencari nilai Tb, fkk, fi, dan ℓ dari tabel data terlebih dahulu. Selanjutnya substitusikan nilai-nilai tersebut ke rumus median data kelompok. Bagaimana cara menghitung median data kelompok ditunjukkan pada penyelesaian untuk berbagai bentuk soal berikut.

Daftar isi:

• Soal 1 – Median dari berat badan siswa adalah ….
• Soal 2 – Median dari data yang disajikan seperti tabel di atas adalah …
• Soal 3 – Median dari nilai lomba matematika tersebut adalah ….
• Soal 4 – Jika nilai median data kelompok adalah 163,5 cm maka nilai k adalah ….
• Soal 5 – Median dari data pada histogram tersebut adalah ….
• Soal 6 – Jika selisih antara data terbesar dan terkecilnya adalah 10 dan modusnya tunggal, maka hasil kali data kedua dan keempat adalah
• Soal 7 – Median terkecil yang mungkin bagi siswa yang memiliki rata-rata nilai 7 dari enam kali tes adalah ….

Baca Juga: Rumus Mean, Median, dan Modus Data Kelompok

Soal 1 – Median dari berat badan siswa adalah ….

Tabel berikut menunjukkan data berat badan 24 siswa.

Median dari berat badan siswa adalah ….
A. 61,5
B. 62
C, 62,5
D. 63,0
E. 63,5

Pembahasan:
Dari soal dapat diketahui data berat badan 24 siswa (n = 24). Jumlah data n = genap, sehingga letak kelas nilai median berada di antara data ke-²⁴/₂ [data ke-12] dan data ke-(ⁿ/₂ + 1) [data ke-13].

Letak kelas nilai median untuk data berat badan 24 siswa berada antara data ke-12 dan ke-13. Pada tabel, letak kelas median berada pada rentang nilai 61 − 63.

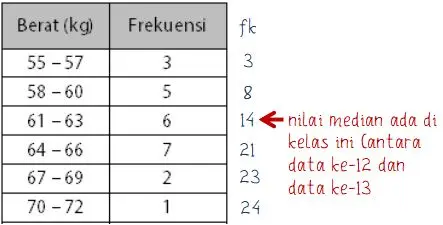
Setelah mengetahui letak kelas nilai median, selanjutnya dapat mencari tahu nilai batas bawah kelas, frekuensi kelas median, frekuensi komulatif kurang dari kelas median, dan panjang kelas.

• Banyak data: n = 24
• Batas bawah kelas median: Tb = 61 – 0,5 = 60,5
• Frekuensi kelas median: fi = 6
• Frekuensi komulatif kurang dari kelas median: fkk = 3 + 5 = 11
• Panjang kelas: ℓ = 63,5 – 60,5 = 3

Cara menghitung median data kelompok:

Jadi, median dari berat badan siswa adalah 62,5

Jawaban: C

Baca Juga: Cara Menghitung Nilai Kuartil Bawah, Tengah, dan Atas Data Kelompok

Soal 2 – Median dari data yang disajikan seperti tabel di atas adalah …

Perhatikan tabel di bawah!

Median dari data yang disajikan seperti tabel di atas adalah ….
A. 32
B. 37,625
C. 38,25
D. 43,25
E. 44,50

Pembahasan:
Banyak data (n) dapat dihitung dengan menjumlahkan frekuensi dari setiap kelas: n = 2 + 8 + 10 + 16 + 12 + 8 + 4 = 60.

Jumlah n = 20 (bilangan genap), sehingga letak kelas nilai median berada antara data ke-⁶⁰/₂ (data ke-30) dan dat ke-⁶⁰/₂+1 (data ke-31). Letak kelas median untuk penyajian data pada tabel tersebut berada di kelas ke-4 (35 – 39).

Setelah mengetahui letak kelas nilai median dapat dicari tahu nilai Tb, n, fkk, fi, dan ℓ seperti berikut.

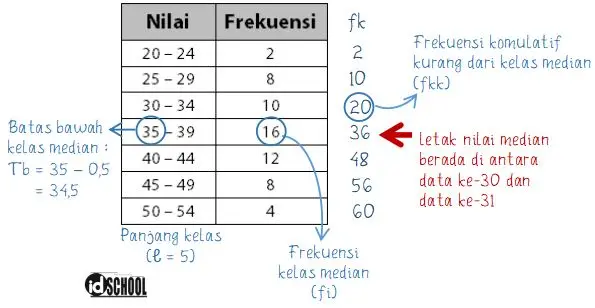
Diketahui beberapa informasi seperti berikut.

• Banyak data: n = 60
• Batas bawah kelas median: Tb = 34,5
• Panjang kelas: ℓ = 39,5 − 34,5 = 5
• Frekuensi kelas letak data median: fi = 16
• Frekuensi komulatif kurang dari kelas median: fkk = 20

Cara menghitung median data kelompok:

Diperoleh nilai median data kelompok dari data pada tabel adalah 37,625. Jadi, median dari data yang disajikan seperti tabel di atas adalah Md = 37,625.

Jawaban: B

Baca Juga: Peluang Suatu Kejadian

Soal 3 – Median dari nilai lomba matematika tersebut adalah ….

Nilai yang diperoleh peserta lomba matematika SMA tahun 2016 disajikan dalam histogram berikut.

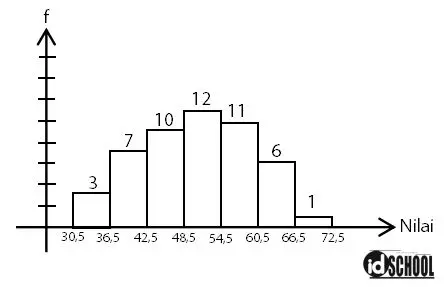
Median dari nilai lomba matematika tersebut adalah ….
A. 51,0
B. 51,5
C. 52,0
D. 52,5
E. 53,0

Pemabahasan:
Banyak data (n): n = 3 + 7 + 10 + 12 + 11 + 6 + 1 = 50. Sehingga letak kelas median berada antara data ke-50/2 (data ke-25) dan data ke-50/2+1 (data ke-26).

Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi berikut.

• Banyak data: n = 50
• Batas bawah kelas median: Tb = 48,5
• Panjang kelas median: ℓ = 54,5 – 48,5 = 6
• Frekuensi kelas median: fi = 12
• Frekuensi komulatif kurang dari kelas median: fkk = 20

Menghitung median data kelompok:

Jadi, median dari nilai lomba matematika tersebut adalah 51,0.

Jawaban: A

Baca Juga: Berbagai Bentuk Soal Mean Data Kelompok dan Pembahasannya

Soal 4 – Jika nilai median data kelompok adalah 163,5 cm maka nilai k adalah ….

Data berikut adalah tinggi badan sekelompok siswa.

Jika nilai median data kelompok adalah 163,5 cm maka nilai k adalah ….
A. 40
B. 42
C. 43
D. 46
E. 48

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi-informasi seperti berikut.

• Banyak data (n):
  n = 5 + 20 + k + 26 + 7
  n = 58 + k
• Nilai median: Md = 163,5
• Panjang kelas: 
  ℓ = 155,5 − 150,5 = 160,5 − 155,5 = … = 165,5 − 160,5 = 5

• Batas bawah kelas median: Tb = 161,0 − 0,5 =160,5
• Frekuensi kelas median: fi = k
• Frekuensi komulatif kurang dari kelas median: fkk = 20 + 5 = 25

Menentukan nilai k (frekuensi kelas median):

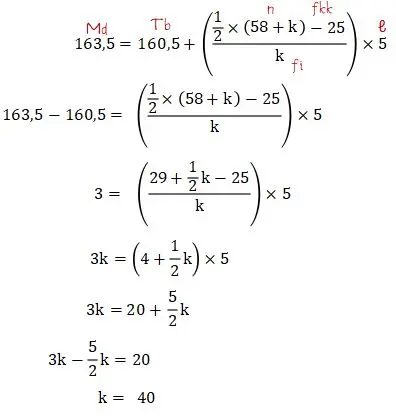
Jadi, jika diketahui nilai median data kelompok adalah 163,5 cm maka nilai k adalah 40.

Jawaban: A

Baca Juga: Simpangan Rata-Rata, Ragam, dan Simpangan Baku

Soal 5 – Median dari data pada histogram tersebut adalah ….

Perhatikan data pada histogram berikut!

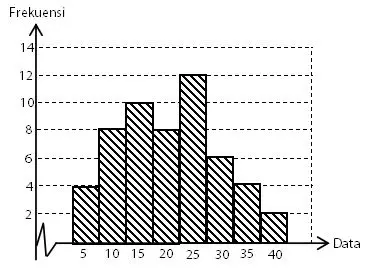
Median dari data pada histogram tersebut adalah ….
A. 17,50
B. 20,63
C. 22,50
D. 27,63
E. 28,50

Pembahasan:
Pertama perlu untuk menghitung banyak data (n): n = 4 + 8 + 10 + 8 + 12 + 6 + 4 + 2 = 54. Dari banyaknya data dapat diketahui di mana letak kelas nilai median.

Diketahui n = 54 (bilangan genap), sehingga letak nilai median berada antara data ke-⁵⁴/₂ (data ke-27) dan data ke-⁵⁴/₂+ 1 (data ke-28).

Dapat diperoleh nilai n, Tb, fi, fkk, dan ℓ seperti berikut.

• Banyak data: n = 54
• Batas bawah kelas median: Tb = 17,5
• Frekuensi kelas median: fi = 8
• Frekuensi komulatif kurang dari kelas median: fkk = 22
• Panjang kelas: ℓ = 5

Menghitung median data kelompok:

Jadi, nilai median dari data pada histogram tersebut adalah 20,63.

Jawaban: B

Soal 6 – Jika selisih antara data terbesar dan terkecilnya adalah 10 dan modusnya tunggal, maka hasil kali data kedua dan keempat adalah

Median dan rata-rata dari data yang terdiri dari empat bilangan asli yang telah diurutkan mulai dari yang terkecil adalah 8.

Jika selisih antara data terbesar dan terkecilnya adalah 10 dan modusnya tunggal, maka hasil kali data kedua dan keempat adalah ….
A. 8
B. 13
C. 24
D. 39
E. 104

Pembahasan:
Berdasarkan keterangan yang diberikan pada soal dapat diperoleh informasi seperti berikut.

• Median = rata-rata = 8
• Selisih antara data terbesar dan terkecil = 10
• Nilai modusnya tunggal (hanya ada satu nilai modus)

Misalkan empat bilangan asli setelah diurutkan berturut-turut adalah a, b, c, dan d. Sehingga, nilai median dapat dinyatakan melalui persamaan berikut.

Median = 8

b + c = 8 × 2 = 16

Diketahui nilai modusnya tunggal sehingga nilai b = c = 8. Sehingga, urutan bilangan menjadi a, 8, 8, dan d. Sehingga,

a + 16 + d = 8 × 4

a + d = 32 – 16 = 16

Diperoleh hasil persamaan a + d = 16 dan diketahui selisih antara data terbesar (d) dan terkecil (a) = 10 adalah 10 (d – a = 10). Cara menentukan nilai a dan d menggunakan metode eliminasi dan substitusi SPLDV (campuran) seperti berikut.

Menentukan nilai d:
a + d = 16
–a + d = 10
———– +
2d = 26

d = 26 : 2 = 13

Menghithung nilai a:

a = 16 – d

a = 16 – 13 = 3

Diperoleh b = 8 dan d = 13, sehingga nilai b × d = 8 × 13 = 104. Jadi, hasil kali data kedua dan keempat adalah 104.

Jawaban: E

Baca Juga: Cara Menghitung Desil dan Persentil Data Kelompok

Soal 7 – Median terkecil yang mungkin bagi siswa yang memiliki rata-rata nilai 7 dari enam kali tes adalah ….

Nilai semua tes matematika dinyatakan dengan bilangan bulat dari 0 sampai 10. Median terkecil yang mungkin bagi siswa yang memiliki rata-rata nilai 7 dari enam kali tes adalah ….
A. 3
B. 4,5
C. 6
D. 7,5
E. 8

Pembahasan:
Berdasarkan keterangan yang diberikan dapat diperoleh informasi-informasi seperti berikut.

• Nilai rata-rata = 7
• Banyaknya tes = 6 kali

Misalkan data dari enam kali tes berturut-turut adalah x₁, x₂, x₃, x₄, x₅, dan x₆ maka akan memenuhi persamaan berikut.

Agar x₃ dan x₄ terkecil maka x5 dan x6 harus terbesar dengan nilai x₅ = 10 dan x₆ = 10.

Sehingga,

x₁ + x₂ + x₃ + x₄ + 10 + 10 = 42

x₁ + x₂ + x₃ + x₄ + 20 = 42

x₁ + x₂ + x₃ + x₄ = 22

Dengan syarat: x₁ ≤ x₂ ≤ x₃ ≤ x₄, maka diperoleh nilai yang mungkin x₁ = 5, x₂ = 5, x₃ = 6, dan x₄ = 6.

Jadi, median terkecilnya adalah: Md = ^{(6 + 6)}/₂ = ¹²/₂ = 6.

Jawaban: C

Demikianlah tadi bagaimana cara menghitung median data kelompok. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Baca Juga: Penyajian Data Bentuk Diagram, Lingkaran, Batang, dan Garis