Nilai mutlak adalah suatu fungsi yang akan membuat fungsi selalui bernilai positif. Penulisan fungsi nilai mutlak di tandai dengan dua buah tanda | yang mengapit fungsi. Persamaan dan pertidaksamaan nilai mutlak memiliki perbedaan pada tanda hubung antara ruas kiri dan kanan. Persamaan nilai mutlak menggunakan tanda sama dengan (=). Sedangkan pertidaksamaan nilai mutlak dapat menggunakan tanda lebih besar (>), lebih besar sama dengan (≥), kurang dari (<), atau kurang dari sama dengan (≤).
Solusi dari persamaan nilai mutlak adalah sebuah nilai, sedangkan solusi dari pertidaksamaan nilai mutlak adalah suatu himpunan yang memuat satu nilai atau lebih. Untuk menyelesaiaan soal pertidaksamaan dan persamaan nilai mutlak, sobat idschool perlu mengetahui bagaimana sifatnya Melalui sifat pertidaksamaan dan persamaan nilai mutlak, sobat idschool dapat menentukan himpunan penyelesaian dari suatu pertidaksamaan nilai mutlak. Bagaimanakah caranya? Cari tahu jawabannya memlalui ulasan di bawah.
Table of Contents
- Persamaan Nilai Mutlak
- Grafik Fungsi Nilai Mutlak
- Sifat Pertidaksamaan Nilai Mutlak
- Contoh Soal dan Pembahasan
- Contoh 1 – Soal Pertidaksamaan Nilai Mutlak Bentuk | ax+b | < c
- Contoh 2 – Nilai Mutlak Bentuk | f(x) > | g(x)
Persamaan Nilai Mutlak
Tanda nilai mutlak disimbolkan dengan dua buah garis lurus yang mengapit suatu nilai atau persamaan yaitu | … |. Persamaan nilai mutlak akan menjadikan nilai di dalam tanda mutlak selalu positif. Dengan kata lain, jika nilai di dalam tanda mutlak lebih kecil dari nol maka nilainya akan tetap menjadi positif.
Misalkan, nilai |2| = 2, |-3| = 3, dan |0| = 0. Secara umum, solusi dari suatu persamaan nilai mutlak secara umum sesuai dengan nilai-nilai berikut.
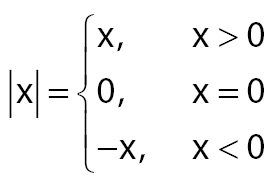
Baca Juga: Pertidaksamaan Kuadrat dan Himpunan Penyelesaiannya
Dalam pertidaksamaan nilai mutlak, besar nilainya dapat meliputi tiga kemungkinan persamaan. Pertama: Jika nilai x di dalam fungsi positif maka nilai sama dengan x. Kedua: Jika nilai x dalam tanda mutlak sama dengan 0 maka nilai x sama dengan 0. Ketiga: Jika nilai x dalam tanda mutlak negatif maka nilai fungsi x sama dengan negatif x.
Dengan kata lain, nilai pada persamaan nilai mutlak akan selalu positif.
Grafik Fungsi Nilai Mutlak
Fungsi nilai mutlak merupakan fungsi yang kontinu. Jika digambarkan dalam bentuk grafik, gambar grafik fungsi nilai mutlak membentuk garis lurus, seperti membentuk huruf v pada interval tertentu. Grafik yang dihasilkan mempunyai satu buah titik puncak dan garisnya simetris, antara ruas kanan dan kiri.
Perhatikan gambar grafik nilai mutlak yang diberikan seperti gambar di bawah.

Baca Juga: Sistem Persamaan Linear Dua Variabel (SPLDV)
Sifat Pertidaksamaan Nilai Mutlak
Dalam pertidaksamaan nilai mutlak terdapat pertidaksamaan aljabar yang ekuivalen dengan pertidaksamaan nilai mutlak. Persamaan ini sering disebut sebagai sifat pertidaksamaan nilai mutlak. Sifat inilah yang dapat digunakan untuk menentukan himpunan penyelesaian pada soal-soal pertidaksamaan nilai mutlak.
Berikut ini adalah sifat-sifat pertidaksamaan nilai mutlak yang dapat digunakan untuk menyelesaikan soal-soal terkait pertidaksamaan nilai mutlak.

Dalam menyelesaikan pertidaksamaan nilai mutlak, selain perlu mengetahui sifa-sifat yang telah diberikan di atas, diperlukan juga kemampuan untuk menguasai cara operasi bentuk aljabar.
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Pertidaksamaan Nilai Mutlak Bentuk | ax+b | < c
Himpunan penyelesaian pertidaksamaan mutlak | 2x + 5 | < 17 adalah ….
A. – 11 < x < 6
B. x < -11 atau x > 6
C. – 22 < x < 12
D. – 6 < x < 11
E. x < – 6 atau x > 11
Pembahasan:
Diberikan sebuah pertidaksamaan |2x + 5| < 17
Berdasarkan sifat pada pertidaksamaan nilai mutlak diperoleh pertidaksamaan – 17 < 2x + 5 < 17.
Selanjutnya dengan menggunakan operasi bentuk aljabar akan diperoleh hasil seperti berikut.
‒17 < 2x + 5 < 17
‒17 ‒ 5 < 2x < 17 ‒ 5
‒22 < 2x < 12
‒22/2 < x < 12/2
‒11 < x < 6
Jadi, himpunan penyelesaian yang sesuai untuk pertidaksamaan 2x + 5 < 17 adalah – 11 < x < 6.
Jawaban: A
Baca Juga: Cara Menyelesaikan Pertidakasamaan Nilai Mutlak Bentuk Pecahan
Contoh 2 – Nilai Mutlak Bentuk | f(x) > | g(x)
Himpunan penyelesaian pertidaksamaan mutlak | x + 5 | > | x – 2 | adalah ….
A. 0 < x < ‒3/2
B. x < 3/2
C. x > 3/2
D. x < ‒3/2
B. x > ‒3/2
Pembahasan:
Berdasarkan ketentuan pada pertidaksamaan nilai mutlak, diperoleh pertidaksamaan dan penyelesaiannya seperti berikut.
| x + 5 | > | x – 2 |
( x + 5)2 > (x ‒ 2)2
x2 + 10x +25 > x2 ‒ 4x + 4
x2 ‒ x2 + 10x + 4x +25 ‒ 4 > 0
14x + 21 > 0
14x > ‒21
x > ‒ 21/14
x > ‒3/2
Sehingga diperoleh himpunan penyelesaian pertidaksamaan mutlak | x + 5 | > | x – 2| adalah x > ‒3/2
Jawaban: E
Demikianlah ulasan materi tentang persamaan dan pertidaksamaan nilai mutlak. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Memahami pertidaksamaan kuadrat
egadwi754@gmail.com
memahami pertidaksamaan kuadratt