Luas daerah yang diarsir pada umumnya adalah bangun datar yang membentuk suatu bentuk tertentu. Bentuk dari luas daerah yang diarsir dapat berupa suatu bangun atau kombonasi/bagian dari suatu bangun. Bangun datar sendiri merupakan bidang dua dimensi yang memiliki ukuran panjang dan lebar.
Ada banyak bidang yang termasuk sebagai bangun datar seperti persegi, persegi panjang, layang-layang, belah ketupat, trapesium, lingkaran, dan lain sebagainya. Untuk beberapa bidang yang telah disebutkan tersebut terdapat rumus umum untuk menghitung luasnya.
Beberapa bidang bangun datar lain dapat juga berbentuk tidak beraturan yang biasanya ditunjukkan melalui luas daerah yang diarsir. Cara menghitung luas daerah yang diarsir tersebut dapat menggunakan rumus luas yang berlaku pada bidang datar. Tentunya rumus yang digunakan perlu disesuaikan dengan bentuk bangunnya. apakah kombinasi dari beberapa rumus atau bagian dari rumus.
Bagaimanakah cara menghitung luas daerah yang diarsir? Sobat idschool dapat mencari jawabannya melalui bahasan di bawah.
Table of Contents
Luas Bangun Datar Beraturan
Bentuk bangun datar beraturan sering kita jumpai di kehidupan sehari-hari, misalnya meja yang biasanya memiliki bentuk persegi, persegi panjang, atau lingkaran. Contoh lain adalah layang-layang yaitu mainan dari kertas yang biasanya dapat diterbangkan karena ada angin. Setiap bangun datar tersebut memiliki luas daerah yang dapat dihitung melalui rumus umumnya.
Besar luas daerah bergantung dari ukuran bangun datar: berapa nilai panjang, lebar, alas, tinggi, atau jari-jari. Luas daerah dari bangun datar tersebut dapat diperoleh melalui rumus umum bangun datar. Beberapa rumus luas bangun datar beraturan dan gambarnya sesuai dengan tabel berikut.
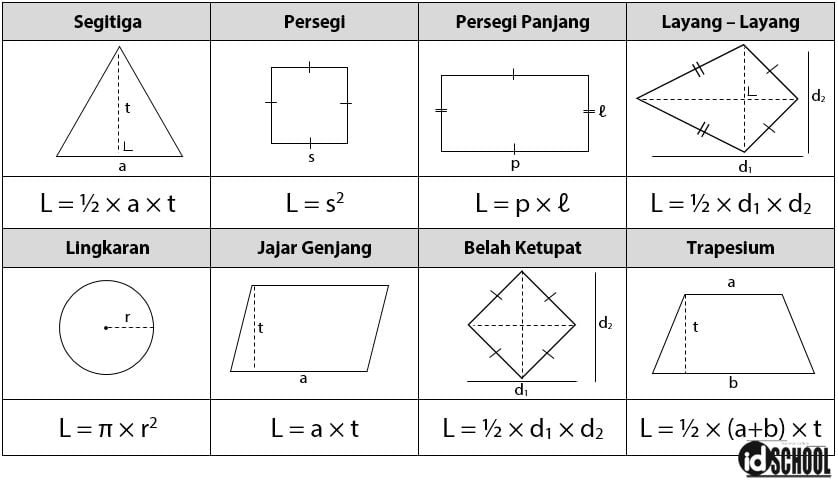
Sobat idschool dapat menggunakan rumus-rumus yang sesuai bentuk bangun untuk menghitung luas daerah dari suatu bangun datar.
Baca Juga: Karakteristik Segitiga dan Segiempat
Luas Daerah yang Diarsir
Bentuk daerah yang diarsir dapat memiliki ragam yang berbeda dan sangat banyak jenisnya. Karena bentuk yang sangat beragam ini, tidak ada rumus umum yang berlaku untuk menghitung luas daerahnya. Namun, luas daerah yang diarsir dapat tetap dihitung menggunakan kombinasi rumus umum bangun datar yang sudah diketahui
Bagaimana caranya?
Sebagai contoh, akan diberikan proses cara menghitung luas daerah yang diarsir untuk sesuatu bangun.
Soal:
Perhatikan daerah yang diarsir seperti gambar berikut.
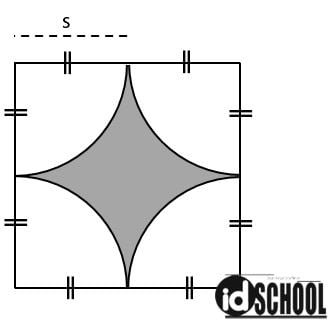
Bagaimana cara menghitung luas daerah tersebut?
Tentu sobat idschool tidak mempunyai rumus umum secara langung untuk menghitung luasnya. Untuk menghitung luasnya, sobat idschool dapat menggunakan kombinas rumus lingkaran dan persegi.
Perhatikan kembali bahwa luas daerah yang diarsir tersebut adalah luas daerah persegi (sisi = 2s) dikurangi 4 luas seperempat lingkaran (jari-jari = s). Atau sama dengan luas persegi dengan panjang sisi 2s dikurangi luas lingkaran dengan panjang jari-jari s.
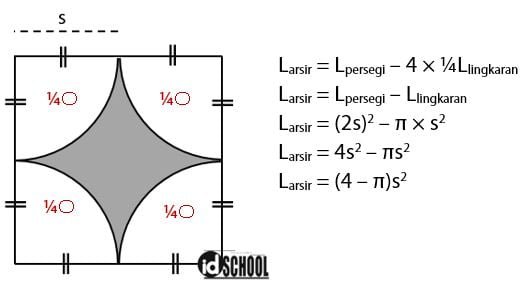
Sehingga diperoleh luas daerah tersebut sama dengan (4 ‒ π)s2.
Baca Juga: Kesebangunan pada Trapesium
Contoh Soal dan Pembahasan
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasil mengerjakan soal. Selamat Berlatih!
Contoh 1 – Soal Menghitung Luas Daerah yang Diarsir
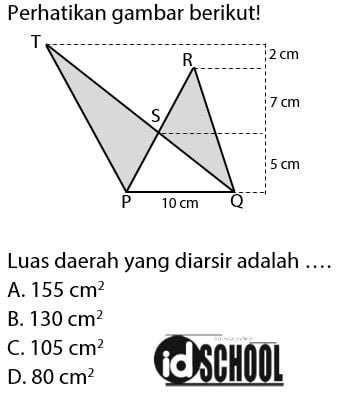
Pembahasan:
Luas daerah yang diarsir terdiri dari dua buah segitiga, yaitu ∆PST dan ∆QRS. Sehingga, untuk menghitung luas daerah yang diarsir perlumenghitung kedua luas segitita tersebut terlebih dahulu.
L∆PST = L∆PQT – L∆PQS
= ½ × 10 × 14 – ½ × 10 × 5
= 70 – 25
= 45 cm2
L∆QRS = L∆PQR – L∆PQS
= ½ × 10 × 12 – ½ × 10 × 5
= 60 – 25
= 35 cm2
Larsir = L∆PST + L∆QRS
= 45 + 35
= 80 cm2
Jadi, luas daerah yang diarsir adalah 80 cm2
Jawaban: D
Baca Juga: Kesebangunan pada Segitiga
Contoh 2 – Soal Menghitung Luas Daerah yang Diarsir
Perhatikan gambar berikut!
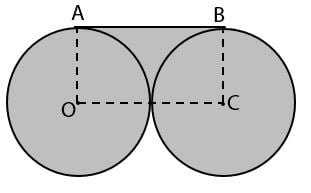
Dua lingakaran dengan pusat O dan C adalah dua lingkaran yang sama. Luas total bangun yang diarsir adalah 329 cm2. Luas persegipanjang OABC adalah ….
A. 231 cm2
B. 129 cm2
C. 98 cm2
D. 68 cm2
Pembahasan:
Perhatikan kembali bangun yang diberikan pada soal!
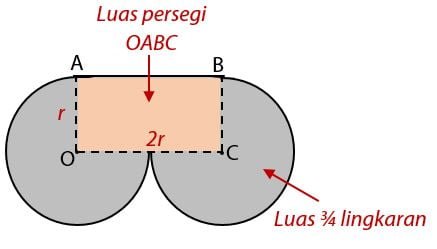
Luas total daerah yang diarsir sama dengan dua kali ¾ lingkaran dan luas persegi OABC.
Larsir = 2 × ¾ LO + LOABC
Larsir = 2( ¾ × π × OA2 ) + (OA × OC)
Larsir = 2( ¾ × π × r2 ) + (r × 2r)
Larsir = 3/2 × 22∕7 × r2 + 2r2
Larsir = 33/7r2 + 2r2
Larsir = 33/7r2 + 14∕7r2
Larsir = 47∕7r2
Menghitng jari – jari:
329 = 47∕7r2
r2 = 7∕47 × 329
r2 = 49
r = 7 cm
Menghitung luas OABC:
LOABC = OA × OC
= r × 2r
= 2r2
= 2 × 72
= 2 × 49
= 98 cm2

Jadi, luas persegipanjang OABC adalah 98 cm2.
Jawaban: C
Baca Juga: Jenis – Jenis Segitiga
Contoh 3 – Soal Menghitung Luas Daerah yang Diarsir
Perhatikan gambar berikut!
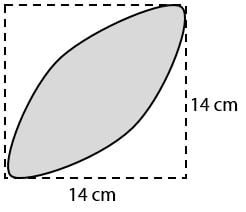
Luas daerah yang diarsir pada gambar di atas adalah … cm2
A. 112
B. 121
C. 144
D. 154
Pembahasan:
Luas yang diarsir merupakan dua kali luas tembereng dari juring seperempat lingkaran. Untuk lebih jelasnya, perhatikan gambar berikut.

Menghitung luas daerah yang diarsir:
Larsir = 2 × Ltembereng
Larsir = 2 × ( ¼π – ½ )r2
Larsir = 2 × ( ¼ × 22/7 – ½ )(142)
Larsir = 2 × (22/28 – ½ )(196)
Larsir = 2 × 8/28 × 196
Larsir = 112 cm2
Jawaban: A
Demikianlah ulasan materi menghitung luas bangun datar yang diarsir yang dilengkapi dengan contoh soal beserta pembahasannya. Terima kasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Luas dan Keliling Lingkaran
Ada ngak yang kls 6 sd
Kak yang persegi panjang ada setengah lingkaran, gak ada kak?
Matematika