Persamaan garis lurus menyatakan sebuah garis lurus dalam bidang koordinat ke dalam sebuah persamaan. Persamaan garis lurus melalui 2 titik dapat dicari atau ditentukan persamaan garisnya. Persamaan garis lurus pada bidang koordinat secara umum dinyatakan melalui bentuk persamaan y = mx + c atau ax + by + c = 0. Ada beberapa cara yang dapat digunakan untuk menentukan persamaan garis lurus. Cara menentukan persamaan garis lurus bergantung pada informasi yang diberikan pada soal.
Salah satu bentuk soal dalam persamaan garis lurus adalah menentukan persamaan garis lurus jika diketahui dua titik yang dilalui garis. Bagaimana cara menentukan persamaan garis lurus jika diketahui dua titik? Melalui halaman ini, sobat idschool dapat mencari tahu caranya. Simak penjelasan lebih lengkapnya melalui ulasan di bawah.
Table of Contents
- Rumus Persamaan Garis Lurus Melalui 2 Titik
- Contoh Soal Menentukan Persamaan Garis Melalui Dua Titik dan Pembahasannya
Rumus Persamaan Garis Lurus Melalui 2 Titik

Sebuah garis lurus diketahui melalui dua titik yaitu (-6, 0) dan (8, 0) seperti yang ditunjukkan seperti gambar garis lurus di atas. Bagaimana persamaan yang sesuai dengan garis lurus yang melalui 2 titik tersebut? Agar dapat menentukan persamaan garis lurus yang melalui 2 titik, sobat idschool membutuhkan bagaimana rumus umum garis lurus yang melalui dua titik.
Misalkan diberikan sebuah garis lurus yang diketahui melalui titik (x1, y1) dan (x2, y2). Cara untuk menentukan persaman garis lurus tersebut dapat melalui persamaan yang dinyatakan dalam rumus persamaan garis lurus melalui 2 titik berikut.

Dengan rumus yang dapat digunakan untuk menentukan persamaan garis lurus melalui 2 titik di atas, sobat idschool dapat menentukan persamaan garis lurus melalui 2 titik pada awal pembahasan. Lihat kembali gambar sebuah garis lurus yang diberikan sebelumnya.
Baca Juga: Cara Mencari Persamaan Garis yang Saling Tegak Lurus
Diketahui bahwa persamaan garis lurus tersebut melalui dua titik yaitu titik (0,8) dan (– 6, 0). Sehingga untuk mendapatkan persamaan garis lurus seperti pada gambar di atas, sobat idschool hanya perlu substitusi nilai dua titik tersebut sebagai (x1, y1) dan (x2, y2) pada persamaan garis lurus yang melalui dua titik. Simak contoh cara menentukan persamaan garis lurus melalui 2 titik seperti cara berikut.
Menentukan persamaan garis lurus yang melalui titik (0,8) dan (–6, 0):
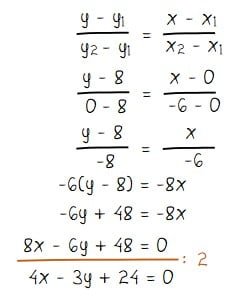
Jadi, persamaan garis lurus tersebut melalui titik (0,8) dan (– 6, 0) adalah 4x – 3y + 24 = 0.
Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel (SPLDV)
Contoh Soal Menentukan Persamaan Garis Melalui Dua Titik dan Pembahasannya
Beberapa contoh soal di bawah dapat sobat idschool gunakan untuk menambah pemahaman bahasan di atas. Setiap contoh soal yang diberikan dilengkapi dengan pembahasannya. Sobat idschool dapat menggunakan pembahasan tersebut sebagai tolak ukur keberhasilan mengerjakan soal. Selamat Berlatih!
Contoh 1 – Menentukan Persamaan Garis Lurus Melalui 2 Titik
Perhatikan gambar di bawah!
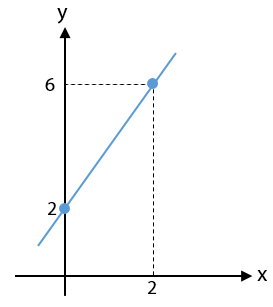
Persamaan garis yang sesuai dengan gambar di atas adalah ….
A. y = 2x + 2
B. y = 2x – 2
C. y = –2x + 2
D. y = –2x – 2
Pembahasan:
Perhatikan bahwa persamaan garis yang diberikan pada soal melalui dua titik yaitu (0, 2) dan (2, 6). Sehingga persamaan garis yang sesuai gambar pada soal.

Jadi, persamaan garis yang sesuai dengan gambar di atas adalah y = 2x + 2.
Jawaban: A
Baca Juga: Cara Menggambar Garis Lurus dari Sebuah Persamaan
Contoh 2 – Menentukan Persamaan Garis Lurus
Persamaan garis yang melalui titik (–2, 4) dan (6, 3) adalah ….
A. x + 8y + 30 = 0
B. x + 8y – 30 = 0
C. x – 8y + 30 = 0
D. x – 8y – 30 = 0
Pembahasan:
Titik yang dilalui garis lurus adalah
- Titik Pertama (– 2, 4) → x1 = –2 dan y1 = 4
- Titik Kedua (6, 3) → x2 = 6 dan y2 = 3
Menentukan persamaan garis yang melalui titik (– 2, 4) dan (6, 3):
y – 4/3 – 4 = x – (–2)/6 – (–2)
y – 4/–1 = x + 2/8
8(y – 4) = –1(x + 2)
8y – 32 = –x – 2
x + 8y – 32 + 2 = 0
x + 8y – 30 = 0
Jadi, persamaan garis yang melalui titik (– 2, 4) dan (6, 3) adalah x + 8y – 30 = 0.
Jawaban: B
Demikianlah tadi ulasan materi cara menentukan persamaan garis melalui 2 titik. Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat.
Baca Juga: Persamaan Garis Lurus