Rumus Mean Median Modus merupakan ukuran pemusatan data. Rumus mean data kelompok terdiri yaitu x̄ = x̄s + Ʃdi·fi/Ʃfi dan x̄ = Ʃxi·fi/Ʃfi. Sementara rumus median data kelompok adalah Md = Tb + [(½n-fkk)/fi]×l. Dan rumus modus data kelompok adalah Mo = Tb + [d1/(d1+d2)]×l.
Mean adalah nilai rata-rata dari data. Median adalah nilai tengah dari data terurut. Dan modus adalah nilai yang sering muncul (memiliki frekuensi paling tinggi). Untuk data tunggal, nilai mean median modus menggunakan rumus berikut.
Median (untuk n bilangan ganjil) = data ke-1/2(n + 1)
Median (untuk n bilangan genap) = 1/2 × [data ke-n + data ke(n + 1)]
Modus → nilai yang paling sering muncul. Atau modus adalah nilai yang frekuensinya paling tinggi.
Ketiga rumus di atas berlaku pada data tunggal. Selanjutnya, untuk rumus mean median modus data kelompok ada di bawah.
Bentuk Penyajian Data Kelompok
Data kelompok memilki kelas-kelas. Setiap kelas memiliki batas atau tepi bawah kelas (Tb), tepi atas kelas, panjang kelas, dan frekuensinya.
- Tepi bawah kelas:
Tb = nilai terendah dari kelas − 0,5 - Tepi atas kelas:
Ta = nilai tertinggi dari kelas + 0,5 - Panjang kelas:
l = Ta − Tb - Frekuensi kelas = banyak data dalam satu kelas
1) Tabel distribusi Frekuensi
Bentuk penyajian data kelompok dalam tabel distribusi frekunesi memiliki dua kolom dan beberapa baris. Satu kolom merupakan data kelas dan satu kolom lain adalah frekuensi.
Contoh penyajian data dalam bentuk tabel distribusi frekuensi:

2) Histogram
Histogram berbentuk diagram batang yang saling berdempetan. Contoh penyajian data dalam bentuk histogram ada pada gambar di bawah.
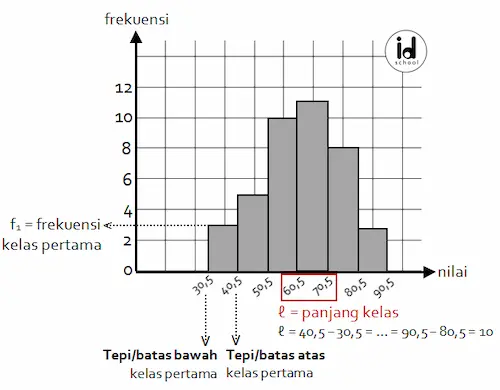
Selain bentuk tabel distribusi frekuensi dan historgam. Data kelompok juga dapat disajikan dalam bentuk lain. Contohnya penyajian dalam bentuk ogive atau pie diagram lingkaran.
Baca Juga: Penyajian Data Dalam Bentuk Ogive Positif dan Ogive Negatif
Rumus Mean Data Kelompok +Contoh Soalnya
Rumus mean data kelompok sama dengan jumlah perkalian nilai tengah setiap kelas dengan frekuensinya dibagi jumlah frekuensi. Nilai tengah setiap kelas adalah setengah dari jumlah nilai batas bawah dan batas atas di setiap kelas.
Rumus mean data kelompok #1:
Atau, dengan notasi sigma dapat dituliskan dalam persamaan berikut.
- Keterangan:
- x̄ = nilai mean (rata-rata) data kelompok
- fi = frekuensi kelas ke-i
- xi = nilai tengah kelas ke-i
Nilai mean data kelompok dapat juga dihitung menggunakan rataan sementara. Misalkan rataan sementara suatu data kelompok adalah xs. Rumus mean data kelompok dapat menggunakan persamaan berikut.
Rumus mean data kelompok #2:
- Keterangan:
- x̄ = nilai mean
- x̄s = rataan sementara
- di = selisih nilai tangah (xi) setiap kelas dengan nilai rataan sementara (x̄s)
- fi = frekuensi kelas ke-i
- ℓ = panjang kelas
Contoh cara menghitung mean data kelompok:
Soal:
Perhatikan data pada tabel berikut!
| Nilai | Frekuensi |
| 31 − 40 | 3 |
| 41 − 50 | 5 |
| 51 − 60 | 10 |
| 61 − 70 | 11 |
| 71 − 80 | 8 |
| 81 − 90 | 3 |
Nilai mean (rata-rata) dari data pada tabel tersebut adalah ….
A. 60,75
B. 61,75
C. 62,75
D. 63,75
E. 64,75
Pembahasan:
Langkah pertama adalah menghitung nilai tengah masing-masing kelas.
Rumus nilai tengah:
Dengan rumus di atas dapat diperoleh nilai tengah setiap kelas yang terdapa pada tabel berikut.
| Kelas | Nilai tengah (xi) |
| 31 – 40 | (40,5 + 30,5) : 2 = 35,5 |
| 41 – 50 | 35,5 + 10 = 45,5 |
| 51 – 60 | 45,5 + 10 = 55,5 |
| 61 – 70 | 55,5 + 10 = 65,5 |
| 71 – 80 | 65,5 + 10 = 75,5 |
| 81 – 90 | 75,5 + 10 = 85,5 |
Hasil perkalian nilai tengah masing-masing kelas dan frekuensinya:
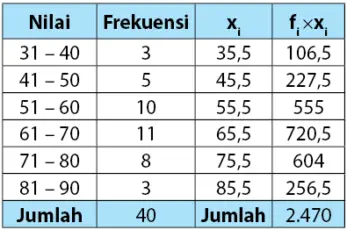
Menghitung nilai rata-rata atau mean data kelompok:
Jadi, nilai mean dari data yang diberikan pada soal adalah 61,75.
Jawaban: B
Untuk cara menghitung mean dengan rataan sementara ada pada halaman penyelesaian soal mean data kelompok ini.
Baca juga kumpulan Soal dan Cara Menghitung Mean Data Kelompok
Rumus Median Data Kelompok +Contoh Soalnya
Median adalah data tengah dari data yang telah diurutkan dari kecil ke besar. Nilai median sama dengan nilai kuartil tengah (Q2). Yaitu nilai yang membagi data menjadi dua bagian sama banyak.
Langkah pertama yang dilakukan adalah menentukan letak kelas median. Setelah mengetahui letak kelas median. Tentukan nilai Tb, fkk, fi, dan l. Selanjutnya, nilai median dihitung menggunakan rumus median data kelompok.
Rumus median data kelompok:
- Keterangan:
- Tb = tepi/batas bawah kelas median
- fkk = frekuensi komulatif kurang dari
- fi = frekuensi kelas median
- ℓ = panjang kelas
Cara mengtahui letak kelas median dibedakan menjadi dua. Yaitu saat banyak data ganjil dan saat banyak data genap.
- Untuk banyak data n = ganjil, median berada pada data ke-(n+1/2).
- Untuk banyak data n = genap, median berada antara data ke-n/2 dan data ke-(n/2 + 1).
Misalnya untuk n = 11 (ganjil). Nilai median adalah data ke-(11+1/2) = data ke-6 dari data yang sudah diurutkan. Untuk banyak data n = 10 (genap). Nilai median sama dengan rata-rata data data ke-(10/2) = data ke-5 dan data ke-(10/2 + 1) = data ke-6 dari data yang sudah diurutkan.
Baca Juga: Ukuran Penyebaran Data (Jangkauan – Hamparan – Kuartil)
Contoh cara menghitung median data kelompok:
Soal:
Perhatikan kembali data pada tabel berikut!
| Nilai | Frekuensi |
| 31 − 40 | 3 |
| 41 − 50 | 5 |
| 51 − 60 | 10 |
| 61 − 70 | 11 |
| 71 − 80 | 8 |
| 81 − 90 | 3 |
Nilai median dari data pada tabel tersebut adalah ….
A. 60,32
B. 61,22
C. 61,32
D. 62,22
E. 62,32
Pembahasan:
Jumlah data yang ada pada tabel adalah 40 (n = genap). Sehingga letak nilai median (Q2) berada antara data ke-20 dan data ke-21.
Cari tahu letak nilai median data kelompok terlebih dahulu.
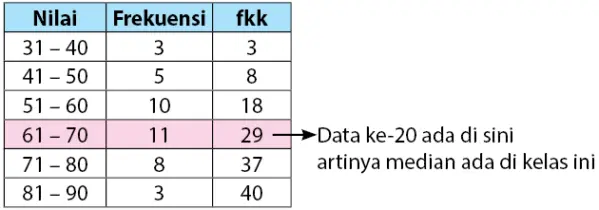
Berdasarkan data pada tabel di atas dapat diperoleh informasi seperti berikut.
- Tepi bawah kelas median:
Tb = 61 – 0,5 = 60,5 - Panjang kelas:
ℓ = 70,5 – 60,5 = 10 - Frekuensi komulatif kurang dari kelas median: fkk = 18
- Frekuensi kelas median: fi = 11
Menghitung nilai median data kelompok:
Jadi, nilai median dari data pada tabel tersebut adalah 62,32.
Jawaban: E
Lihat juga kumpulan soal dan cara menghitug median data kelompok
Rumus Modus Data Kelompok +Contoh Soalnya
Modus adalah nilai yang paling sering muncul. Atau, modus adalah nilai yang memiliki frekuensi paling tinggi (paling besar). Nilai modus data kelompok terdapat pada kelas yang memiliki frekuensi paling tinggi.
Rumus modus data kelompok:
- Keterangan:
- Tb = tepi bawah kelas modus
- d1 = selisih frekuensi kelas modus dengan frekuensi sebelum kelas modus
- d2 = selisih frekuensi kelas modus dengan frekuensi setelah kelas modus
- ℓ = panjang kelas
Cara menghitung modus data kelompok:
Soal:
Perhatikan kembali tabel data kelompok pada tabel!
| Nilai | Frekuensi |
| 31 − 40 | 3 |
| 41 − 50 | 5 |
| 51 − 60 | 10 |
| 61 − 70 | 11 |
| 71 − 80 | 8 |
| 81 − 90 | 3 |
Modus dari data pada tabel kelompok di atas adalah ….
A. 62,5
B. 63,0
C. 63,5
D. 64,0
E. 64,5
Pembahasan:
Dari tabel diketahui kelas yang memiliki frekuensi tertinggi adalah kelas keempat. Interval nilai modus di kelas keempat adalah 61 − 70.
Menentukan nilai Tb, ℓ, d1, dan d2:
- Tebi bawah kelas modus:
Tb = 61 – 0,5 = 60,5 - Panjang kelas:
ℓ = 70,5 – 60,5 = 10 - Selisih frekuensi kelas modus dengan frekuensi sebelum kelas modus: d1 = 11 – 10 = 1
- Selisih frekuensi kelas modus dengan frekuensi setelah kelas modus: d2 = 11 – 8 = 3
Menghitung nilai mdus data kelompok:
Jadi, modus dari data yang disajikan pada diagram batang di atas adalah 46,5.
Jawaban: B
Lihat juga kumpuan soal dan cara menghitung modus data kelompok
Demikian pembahasan mengenai rumus mean median modus data kelompok. Terima kasih sudah mengunjungi idschool.net, semoga bermanfaat!

Jujurly sangat membantu, dapet guru mtk yang gapernah ngulang , mau ujian tanya kisi² dikasih sederhana , eh ternyata kelas lain dikasih kisi² yg lebih rinci . Jarang masuk sekali masuk kasih ppt doangg bentar doang gaada setengah jam. Padahal masuk kelas lain beliau enjoy sampe mapel habis.
Tetep semangat ya sekolahnya (:
yang komen tahun 2020 semua😭
ngakak semua lagi🗿
kalo untuk mencari modus, letak modusnya itu nilai yg terakhir ga ada frekuensi setelahnya itu gimana cara mencari d2nya
Halo Sintia,
Untuk pengerjaan modus coba cari tahu contoh pengerjaan berbagai tipe soal modus https://idschool.net/sma/kumpulan-soal-dan-cara-menghitung-modus-data-kelompok/ (khususnya perhatikan contoh nomor 5)
Untuk cara menghitung d2 (nilai desil ke – 2) bisa dilihat pada halaman https://idschool.net/sma/cara-menghitung-desil-dan-persil-data-kelompok/
Semoga membantu!
bagaimana kalau mencari median data kelompok tapi tidak ada / menemukan tepi bawah pada nilai di tabel? Terimakasih
Halo Hanna, nilai tepi bawah kelas itu dihitung dari nilai terendah pada kelas tersebut dikurangi 0,5. Semoga membantu!
gile, gw bacanya serasa baca buku komedian wkwk
Halo Krisnauli_, terimakasih komentar dan kunjungannya. Admin idschool siap menampung koreksi/kiritk/saran untuk memberikan konten yang lebih baik :)
Susah amat sih anjing
Terimakasih sangat membantu👍😃
Saya sangat membenci pelajran ini
Iya saya juga membencinya
Hmmmm
Untuk Contoh 3 – Cara mencari modus data kelompok >>> panjang interval kelasnya bukannya 10 ya Kak?
Halo Nana, panjang kelas pada contoh 3 adalah 5, misalnya pada kelas pertama: 30-34 ada lima nilai yang termuat yaitu 30, 31, 32, 33, dan 34 (ada 5).
Gimana cara ngitung modus kalau panjang kelasnya tidak beraturan?
Gaada panjanh kelas yang tidak beraturan
jangan lupa mampir ke instagram @wisnuadinn3k3
terimakasihhh
Faedahnya ngitung ginian buat apa sih dikehidupan sehari hari??kan nggak guna banget
buat dapet ijazah bro… klo gk guna ngapain lu sekola jg
matematika ilmu yang menyenangkan~~~
Matematika ilmu yang mematikan, jangan rajin belajar matematika, ayoooooooooooooooooooooo
Kalau lu kerja di perusahaan lu pasti tau tujuannya
Semangat truss jgn lupa tersenyum
Pelajaram matematika sangat bermanvaat
Gg ( ngak guna )
“ngak” apaan bro?
Mkasih pnjelasannya…fghting MTK
ikn hiu mkn tmat = GblG
pasti ngana bangka dada kong ba jamping jamping